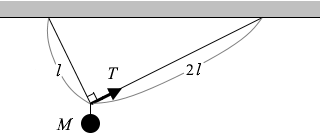
図5のように、長さ l と 2l の2本の糸で質量 M のおもりを水平な天井からつるした。このとき、2本の糸のなす角度は 90° であった。長さ 2l の糸の張力の大きさ T を式で表わせ。ただし、重力加速度の大きさを g とする。
#センター12本試
図5のように、長さ l と 2l の2本の糸で質量 M のおもりを水平な天井からつるした。このとき、2本の糸のなす角度は 90° であった。長さ 2l の糸の張力の大きさ T を式で表わせ。ただし、重力加速度の大きさを g とする。
#センター12本試
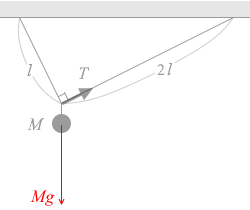おもりには Mg の重力が掛かっています。
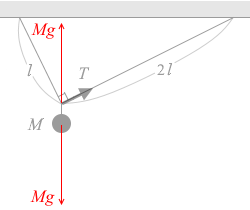おもりが動かず静止しているということは、上向きの同じ大きさの力で支えられているということです。
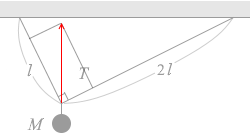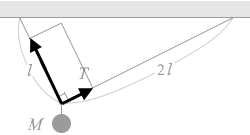この上向きの Mg の力は、2つの張力の合力です。2つの張力を平行四辺形の法則によって足し合わせたものが上向きの Mg です。
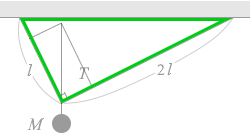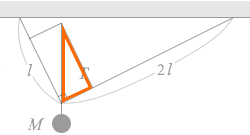そして、左図の緑の三角形とオレンジの三角形は相似です。
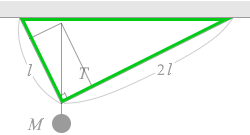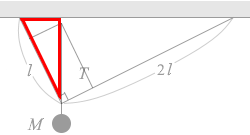緑の三角形と赤の三角形は1つの角を共有した直角三角形同士なので相似であり、
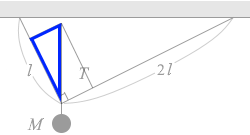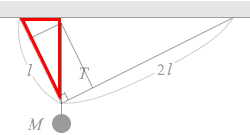赤の三角形と青の三角形も1つの角を共有した直角三角形同士なので相似であり、
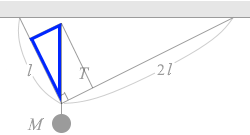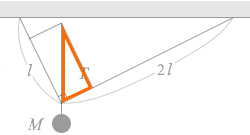青の三角形とオレンジの三角形は錯角が等しいので相似（合同）であり、
結局、緑の三角形とオレンジの三角形は相似になります。
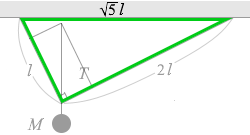緑の三角形の長い辺の長さは、三平方の定理より、
x2 = l2 + (2l)2
を解いて、\(\sqrt{5}\) l であるので、
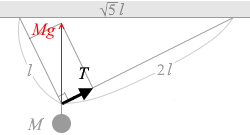\(\large{\frac{T}{Mg}}\) = \(\large{\frac{l}{\sqrt{5}l}}\)
∴ T = \(\large{\frac{1}{\sqrt{5}}}\)Mg
（余談）
もし、糸の長さが l と \(\sqrt{3}\) l であれば、
T = Mg × sin30° = \(\large{\frac{1}{2}}\)Mg
と、暗算ですぐ解けます。