(問5)W は「気体が外部からされた仕事」と定義されているので、気体が外部に仕事をした場合にはこれは負、ということになります。Q に関しては「気体が外部から吸収した熱量」と定義されているので、そのまま正、ということになります。
答えは W は負、Q は正。
仕事 W は2通りの定義の仕方があり 、注意が必要です。
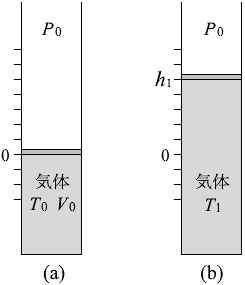
(問6)T 1 のときの気体の体積を V 1 、気体の温度が T のときの気体の体積を V と置くと、シャルルの法則 *
\(\large{\frac{V_1}{T_1}}\) = \(\large{\frac{V_2}{T_2}}\)ボイル⋅シャルルの法則 より、閉じる
\(\large{\frac{V_0}{T_0}}\) = \(\large{\frac{V_1}{T_1}}\) = \(\large{\frac{V}{T}}\)
目盛り 0 の高さを h 0 と置くと、上式は以下のように書き変えられ、
\(\large{\frac{h_0S}{T_0}}\) = \(\large{\frac{(h_0+h_1)S}{T_1}}\) = \(\large{\frac{(h_0+h)S}{T}}\)
∴ \(\large{\frac{h_0}{T_0}}\) = \(\large{\frac{(h_0+h_1)}{T_1}}\) = \(\large{\frac{(h_0+h)}{T}}\)
この式をこねくり回して、自分で設定した h 0 を消去しますと、
\(\large{\frac{h_0}{T_0}}\) = \(\large{\frac{(h_0+h_1)}{T_1}}\) より、
h 0 T 1 = (h 0 + h 1 )T 0
∴ h 0 (T 1 - T 0 ) = h 1 T 0
∴ h 0 = \(\large{\frac{h_1T_0}{T_1-T_0}}\) ……➊
\(\large{\frac{h_0}{T_0}}\) = \(\large{\frac{(h_0+h)}{T}}\) より、
h 0 T = (h 0 + h )T 0
∴ h 0 (T - T 0 ) = h T 0
∴ h 0 = \(\large{\frac{hT_0}{T-T_0}}\) ……➋
➊式、➋式より、
\(\large{\frac{hT_0}{T-T_0}}\) = \(\large{\frac{h_1T_0}{T_1-T_0}}\)
∴ \(\large{\frac{h}{T-T_0}}\) = \(\large{\frac{h_1}{T_1-T_0}}\)
∴ h = \(\large{\frac{T-T_0}{T_1-T_0}}\)h 1
答えは ③ です。
(別解)
\(\large{\frac{ΔV_1}{ΔT_1}}\) = \(\large{\frac{ΔV}{ΔT}}\)
⇔ \(\large{\frac{(h_1-0)S}{T_1-T_0}}\) = \(\large{\frac{(h-0)S}{T-T_0}}\)
∴ \(\large{\frac{h_1}{T_1-T_0}}\) = \(\large{\frac{h}{T-T_0}}\)
∴ h = \(\large{\frac{T-T_0}{T_1-T_0}}\)h 1
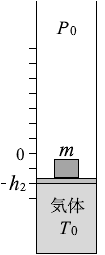
(問7)P 0 です。そして、十分に時間がたった後の気体の圧力を P 2 、体積を V 2 とすると、ボイルの法則 より、
P 0 V 0 = P 2 V 2
気体の圧力 P 2 は、大気圧とおもりによる圧力を合わせたものとつり合っています。おもりによる圧力というのは \(\large{\frac{mg}{S}}\) です。つまり、
P 2 = P 0 + \(\large{\frac{mg}{S}}\)
体積 V 2 については
V 2 = V 0 - h 2 S
よって、
P 0 V 0 = P 2 V 2
= \(\Big(\)P 0 + \(\large{\frac{mg}{S}}\)\(\Big)\)(V 0 - h 2 S )