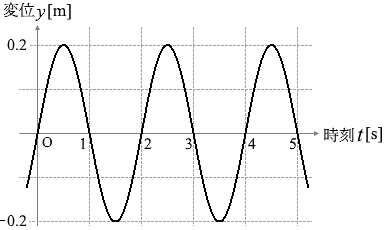
x軸の正の向きに速さ 2m/s で進む正弦波がある。図3は x = 0 における、変位 y [m] と時刻 t [s] の関係を表している。位置 x [m] における、時刻 t [s] での変位 y [m] を表す式として最も適当なものを、下の①～⑧のうちから一つ選ベ。
① 0.2sin{π(t + 2x)} ② 0.2sin{π(t - 2x)}
③ 0.2sin\(\Big\{\)π(t + \(\large{\frac{x}{2}}\))\(\Big\}\) ④ 0.2sin\(\Big\{\)π(t - \(\large{\frac{x}{2}}\))\(\Big\}\)
⑤ 0.2sin{2π(t + 2x)} ⑥ 0.2sin{2π(t - 2x)}
⑦ 0.2sin\(\Big\{\)2π(t + \(\large{\frac{x}{2}}\))\(\Big\}\) ⑧ 0.2sin\(\Big\{\)2π(t - \(\large{\frac{x}{2}}\))\(\Big\}\)
#センター16本試物理
まず、波のグラフを見るときは横軸が x か t かを確認しなければいけません。図3の横軸は t です。
振幅を A 、周期を T と置きますと、グラフより A = 0.2 [m] 、T = 2 [s] です。
y = Asin\(\large{\frac{2π}{T}}\)\(\big(\)t - \(\large{\frac{x}{v}}\)\(\big)\)
と表せますので各値を代入しますと、
y = 0.2sin\(\large{\frac{2π}{2}}\)\(\big(\)t - \(\large{\frac{x}{2}}\)\(\big)\)
= 0.2sin\(\Big\{\)π(t - \(\large{\frac{x}{2}}\))\(\Big\}\)
答えは ④ です。
（注意）
波長を λ と置きますと、λ = vT
波の基本式
f = \(\large{\frac{1}{T}}\)
v = fλ
より
λ = vT
であるので、λ = 2×2 = 4 [m] です。もし、図3の横軸を x [m] であると読み間違えると、λ = 2 [m] としてしまうことになります。
それと、正弦波の式はそのままでは暗記しにくいので、導出方法ごと暗記してください。
正弦波の各点は
y = Asinωt
という単振動の動きをし、ω = \(\large{\frac{2π}{T}}\) であるので
y = Asin\(\large{\frac{2π}{T}}\)t
となり、時間が \(\large{\frac{x}{v}}\) 遅れるので
y = Asin\(\large{\frac{2π}{T}}\)\(\big(\)t - \(\large{\frac{x}{v}}\)\(\big)\)
となります。λ を含むように書き変えるなら λ = vT なので、
y = Asin2π\(\big(\)\(\large{\frac{t}{T}}\) - \(\large{\frac{x}{λ}}\)\(\big)\)
です。