次の文章中の空欄ウ⋅エに入れる式の組合せとして最も適当なものを、下の①~④のうちから一つ選べ。
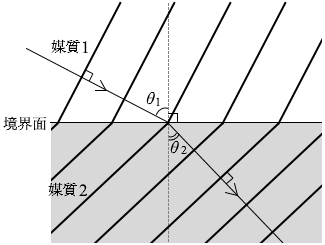
図4は、平面波が媒質1から境界面に入射し、屈折して媒質2の中を進む様子を示している。太い実線は、ある時刻における入射波と屈折波の山の波面を表している。入射角は θ1 、屈折角は θ2 である。
このとき、媒質1と媒質2での波の速さをそれぞれ v1 、v2 とすると、図4のように θ1 > θ2 のときは、ウの関係があることがわかる。また、v1 、v2 、θ1 、θ2 の間には \(\large{\frac{v_1}{v_2}}\) = エの関係式が成り立つ。
| ① | ② | ③ | ④ | |
|---|---|---|---|---|
| ウ | v1 > v2 | v1 > v2 | v1 < v2 | v1 < v2 |
| エ | \(\large{\frac{\sinθ_1}{\sinθ_2}}\) | \(\large{\frac{\sinθ_2}{\sinθ_1}}\) | \(\large{\frac{\sinθ_1}{\sinθ_2}}\) | \(\large{\frac{\sinθ_2}{\sinθ_1}}\) |
#センター12本試