波の屈折
波の屈折
波の進む速さというものは、媒質の種類によって変わります。（『媒質による音速』参照）
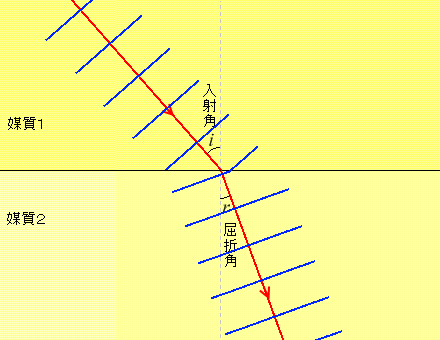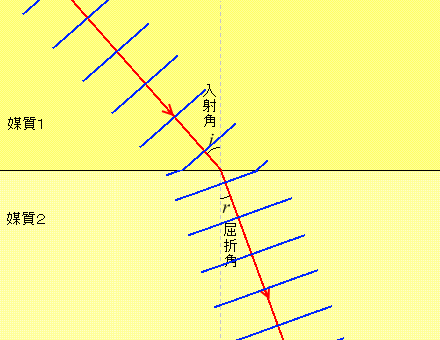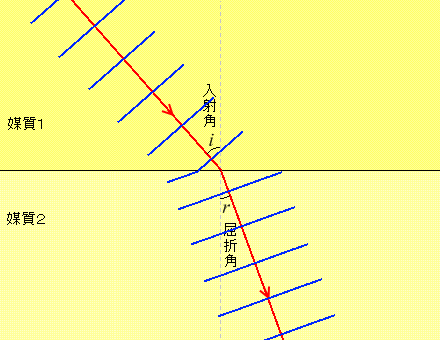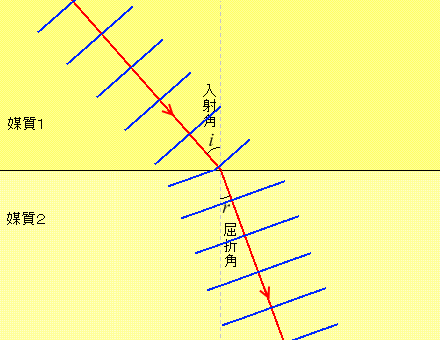そして、ある媒質から別の媒質へと波が進む場合、進む速さが変わることによって、進む方向も変わります
ただし、境界面に対して垂直に進む波は媒質が変わっても進む方向は変わりません。変わりようがありません。
。境界面を境にして進行方向が変わることを波の屈折といいます。
このとき境界面の法線と入射波の進む向きとのなす角（左図では \(i\) の部分。incidence）を入射角といい、境界面の法線と屈折波（境界面で進行方向が変わった波）の進む向きとのなす角（左図では \(r\) の部分。refraction）を屈折角といいます。境界面とのなす角ではなく法線とのなす角であることに注意してください（前項の波の反射と同じです）。 \(i\) と \(r\) は覚えにくいですが、\(i\) についてだけでも「\(i\) は in だから入射」と覚えてください。
屈折の法則
入射角を \(i\) 、屈折角を \(r\) 、媒質1における波の速さを \(v_1\) 、媒質2における波の速さを \(v_2\) としますと、これらの間には以下の関係があります。
\({\large\frac{\sin i}{\sin r}} = {\large\frac{v_1}{v_2}}\)
入射角の正弦と屈折角の正弦の比が、それぞれの媒質での波の速さの比になるのです。この関係を屈折の法則またはスネルの法則 17世紀のオランダの数学者 ヴィレブロルト・スネル が発見しました といいます。
波の速さは媒質の種類によって決まります 音波なのか光波なのか等によって波の速さは違いますが、ここでいっているのは、音波なら音波で媒質の種類が決まればその中を通る波の速さは決まっている、ということです。たとえば、音波の速さは空気の中では 340m/s で、水の中では 1500m/s です。 。媒質の種類が決まっていれば \({\large\frac{v_1}{v_2}}\) の値も決まります。この値を \(n_{12}\) とおき なぜ量記号に \(n\) を用いるかわかりません。何の頭文字だろう？… 、
\({\large\frac{v_1}{v_2}} = n_{12}\)
これを相対屈折率あるいは媒質1に対する媒質2の屈折率と呼びます。（『相対屈折率と絶対屈折率』参照）
屈折の法則（スネルの法則）
\(\boldsymbol{{\Large\frac{\sin i}{\sin r}} = {\Large\frac{v_1}{v_2}} = n_{12} = 一定}\)
媒質1と媒質2が決まっているとき、入射角によって屈折角が変化します。その値は屈折の法則により導き出されます。入射角が小さくなれば屈折角も小さくなります。入射角が小さくなるのに屈折角が大きくなるというようなことは起こりません。
媒質1と入射角が決まっているとき、媒質2によって屈折角が変化します。その値は屈折の法則により導き出されます。媒質2における波の速さが大きくなれば屈折角も大きくなります。媒質2における波の速さが大きくなるのに屈折角が小さくなるというようなことは起こりません。
このイラストのイメージは音波のときと光波のときでは逆になります。音波は固い媒質の方が伝わる速さがおおむね速く、光波は固い媒質の方が伝わる速さがおおむね遅いです。
逆のとき
波の進行方向が逆向きだったり（あるいは媒質1と媒質2が入れ替わってたり）するときは、相対屈折率は、（分母分子が逆転して）
\({\large\frac{\sin r}{\sin i}} = n_{21}\)
であり、\(n_{12}\) の逆数となります。
\(n_{21}\) = \({\large\frac{1}{n_{12}}}\)
です。
覚え方
屈折の法則の式は分母分子を取り違いやすいので、
と、頭の中で矢印を付与して覚えてください。（『光の屈折』の『覚え方』も参照）
ホイヘンスの原理により導かれる
屈折の法則はホイヘンスの原理により導かれます。
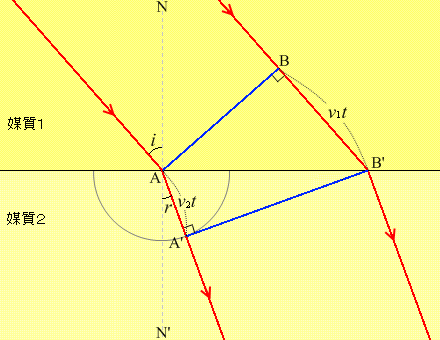左図において、媒質1での波の速さを \(v_1\) 、媒質2での波の速さを \(v_2\) 、ABを入射波の波面とし、波がBからB'に進む時間を \(t\) とします。すると、BB'の距離は \(v_1t\) であり、この \(t\) の間にAから出た素元波が進む距離は \(v_2t\) です。
この素元波が描く半円にB’から接線を引き、その接点をA’とすると、半径と接線は直角に交わるから ∠AA'B'は直角です。
そして、
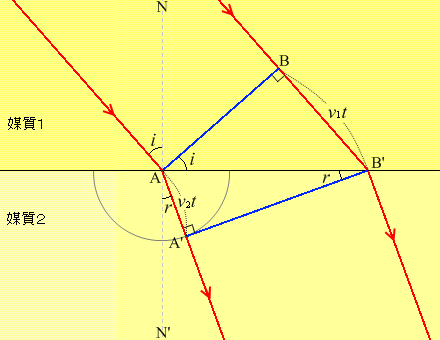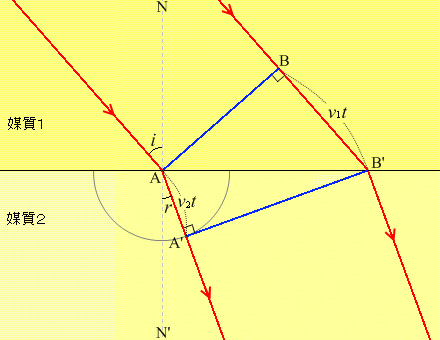
入射角 \(i\) = 90° - ∠NAB であり、
∠BAB' = 90° - ∠NAB であるので、
∠BAB' = \(i\)
です。また、
屈折角 \(r\) = 90° - ∠B'AA' であり、
∠AB'A' = 90° - ∠B’AA' であるので、
∠AB'A' = \(r\)
です。
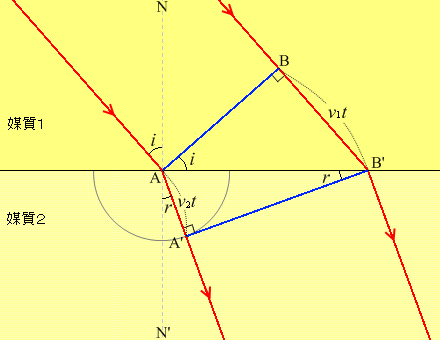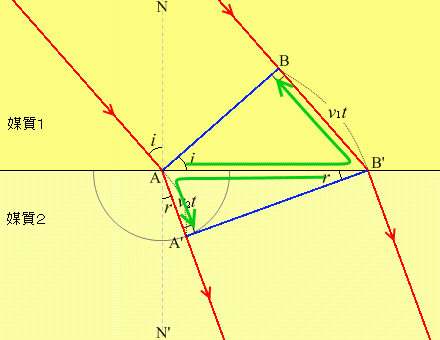そうしますと、
sin \(i = {\large\rm{\frac{B'B}{AB'}}}\)
sin \(r = {\large\rm{\frac{AA'}{AB'}}}\)
ゆえに、
\({\large\frac{\sin i}{\sin r}} = {\rm{\large\frac{\frac{B'B}{AB'}}{\frac{AA'}{AB'}}}} = {\large\frac{\rm{B'B}}{\rm{AA'}}} = {\large\frac{v_1 t}{v_2 t}} = {\large\frac{v_1}{v_2}}\)
となり、屈折の法則が導かれます。
屈折波の波面
次に波面ABが屈折すると本当に波面A'B'になるのかどうかを説明します。
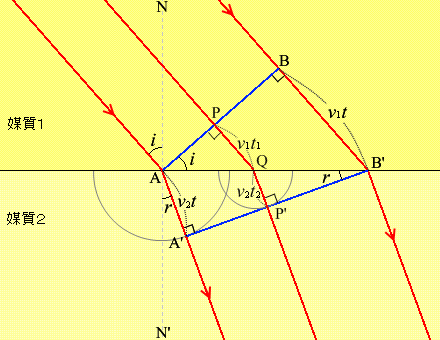波面AB上の任意の点Pが境界面上の点Qに達するまでの時間を \(t_1\) 、点QからA'B'に下ろした垂線の足を点P'としたときに波がQからP'まで進む時間を \(t_2\) とします。
PQ∥BB' であるから、
\({\large\rm{\frac{PQ}{BB'}}} = {\large\rm{\frac{AQ}{AB'}}} = {\large\rm{\frac{AB'-QB'}{AB'}}}\)
\(= 1 - {\large{\rm\frac{QB'}{AB'}}}\) \({\large(}\) QP'∥AA' であるので \({\large{\rm\frac{QB'}{AB'}}}\)=\({\large\rm{\frac{QP'}{AA'}}}\) \({\large)}\)
\(= 1 - {\large{\rm\frac{QP'}{AA'}}}\)
つまり、
\({\large\rm{\frac{PQ}{BB'}}} = 1 - {\large\rm{\frac{QP'}{AA'}}}\)
∴ \({\large\rm{\frac{PQ}{BB'}}} + {\large\rm{\frac{QP'}{AA'}}}= 1\)
∴ \({\large\frac{v_1 t_1}{v_1 t}} + {\large\frac{v_2 t_2}{v_2 t}}= 1\)
∴ \({\large\frac{t_1}{t}} + {\large\frac{t_2}{t}}= 1\)
∴ \(t_1 + t_2 = t\)
となり、これは点Pにいる波が時間 \(t\) だけ経つと点P'に来る、ということです。点PはAB上の任意の点であると定義しました。任意の点で成り立つということはあらゆる点で成り立つということです。つまり、AB上のあらゆる点は \(t\) だけ経つとA'B'上にたどり着くということです。すなわち、波面ABは \(t\) だけ経つと波面A'B'になる、といえます。
境界面を通過するときに振動数は変わらない
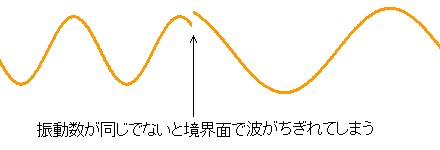波が媒質1から媒質2へと進むとき、振動数（周波数）は変化しません。振動数が同じでないと境界面で波がちぎれてしまいます。波がちぎれてしまっては波が進行したとはいえなくなってしまいます。
変わるのは波の速さと波長です。波の基本式 \(v = fλ\) のうちの \(v\) と \(λ\) です。日常生活では \(v\) が変化することはなかなか感じ取れないので、これは想像するのが難しいかもしれません。
屈折の法則の式をもう少し拡張
屈折の法則の式に \(v = fλ\) を代入しますと、
\({\large\frac{\sin i}{\sin r}} = {\large\frac{v_1}{v_2}} = {\large\frac{fλ_1}{fλ_2}} = {\large\frac{λ_1}{λ_2}}\)
となりますので、相対屈折率は波長の比に等しいともいえます。
屈折の法則（スネルの法則）
\(\boldsymbol{{\Large\frac{\sin i}{\sin r}} = {\Large\frac{v_1}{v_2}} = {\large\frac{λ_1}{λ_2}} = n_{12} = 一定}\)
最短距離？
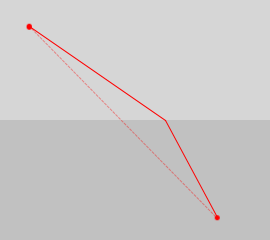波が屈折して進む経路は、実は、進むのに掛かる時間が最小となるような経路になっています。フェルマーの原理とか最小作用の原理とか変分原理などと呼ばれています。
車が舗装道路の領域と砂利道の領域とを進む場合、真っ直ぐな経路をとるよりも、舗装道路の経路を長めにとって砂利道の経路を短めにとる（屈折した経路をとる）方が、早く目的地に到着します。