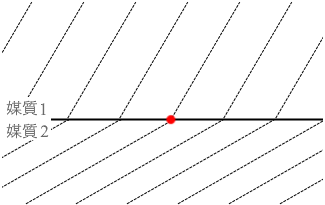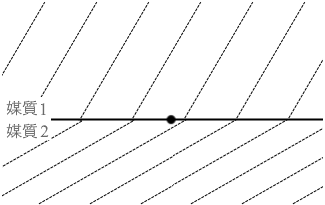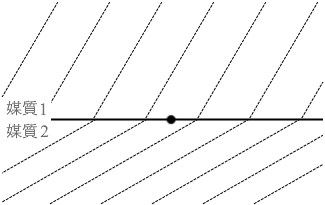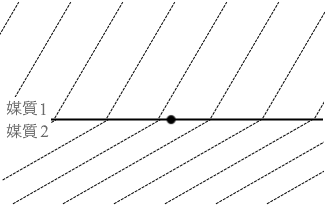
媒質1から入射した平面波が境界面で屈折し、媒質2を伝藩している。ある時刻における波の様子を図1に示す。図中の破線は平面波の山の位置を表しており、媒質1、2において破線が境界面となす角度をそれぞれ θ1 、θ2 、境界面上での山の間隔を d とする。また、媒質1、2での波の速さをそれぞれ v1 、v2 、波長をそれぞれ λ1 、λ2 とする。
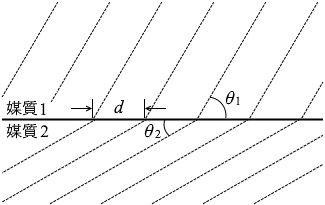
(問1)境界面上の一点において、単位時間あたりに、媒質1から到達する波の山の数と媒質2へと出ていく波の山の数とは等しい。このことから成立する関係として正しいものを、次の①~⑥のうちから一つ選べ。
① v1λ1sinθ1 = v2λ2sinθ2 ② v1λ1cosθ1 = v2λ2cosθ2 ③ \(\large{\frac{v_1\sinθ_1}{λ_1}}\) = \(\large{\frac{v_2\sinθ_2}{λ_2}}\) ④ \(\large{\frac{v_1\cosθ_1}{λ_1}}\) = \(\large{\frac{v_2\cosθ_2}{λ_2}}\) ⑤ v1λ1 = v2λ2 ⑥ \(\large{\frac{v_1}{λ_1}}\) = \(\large{\frac{v_2}{λ_2}}\)
(問2)境界面上での山の間隔 d が媒質1と2において共通であることから成立する関係として正しいものを、次の①~⑦のうちから一つ選べ。
① λ1sinθ1 = λ2sinθ2 ② \(\large{\frac{λ_1}{\sinθ_1}}\) = \(\large{\frac{λ_2}{\sinθ_2}}\) ③ λ1cosθ1 = λ2cosθ2 ④ \(\large{\frac{λ_1}{\cosθ_1}}\) = \(\large{\frac{λ_2}{\cosθ_2}}\) ⑤ λ1tanθ1 = λ2tanθ2 ⑥ \(\large{\frac{λ_1}{\tanθ_1}}\) = \(\large{\frac{λ_2}{\tanθ_2}}\) ⑦ λ1 = λ2
#センター15本試物理Ⅰ #センター15本試物理
 単位時間あたりの山の数というのは
単位時間あたりの山の数というのは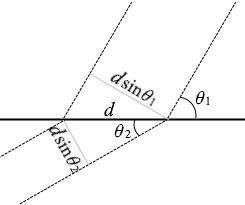 λ1 、λ2 を d を用いて表すと、
λ1 、λ2 を d を用いて表すと、