図3のように、凸レンズの二つの焦点F1、F2の間に物体ABを置くと、正立の虚像ができた。ここで、直線PQは光軸であり、直線LMはレンズの中心点Oと点Bを通る直線である。虚像の大きさは物体の大きさの何倍か。
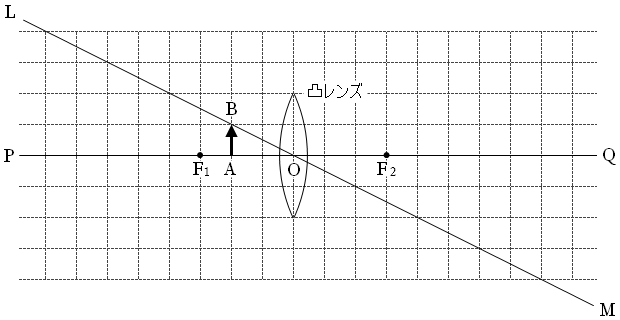
#センター99本試
図3のように、凸レンズの二つの焦点F1、F2の間に物体ABを置くと、正立の虚像ができた。ここで、直線PQは光軸であり、直線LMはレンズの中心点Oと点Bを通る直線である。虚像の大きさは物体の大きさの何倍か。

#センター99本試
この問題は『凸レンズ』項の『物体を焦点より近くに置いたとき』に相当します。
\(\large{\frac{1}{a}}\) + \(\large{\frac{1}{b}}\) = \(\large{\frac{1}{f}}\)
m = \(\large{\frac{|b|}{a}}\)
に各値を当てはめて倍率 m を求めてみます。
焦点距離(凸レンズにおいては正)を f = 3x と置きますと、グラフより、物体とレンズとの距離(常に正)は a = 2x となり、これらの値を上の公式に代入しますと、
\(\large{\frac{1}{2x}}\) + \(\large{\frac{1}{b}}\) = \(\large{\frac{1}{3x}}\) 両辺に 6bx を掛けて
∴ 3b + 6x = 2b
∴ b = - 6x
よって、
m = \(\large{\frac{|b|}{a}}\) = \(\large{\frac{|- 6x|}{2x}}\) = 3
(別解)
この問題は作図によって解くこともできます。
『レンズによる像』の(凸レンズ)の(1)より、光軸に平行な光線は、凸レンズを通った後、焦点を通るので、以下のようになり、
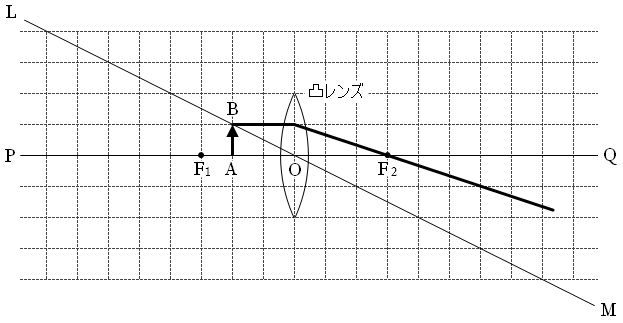
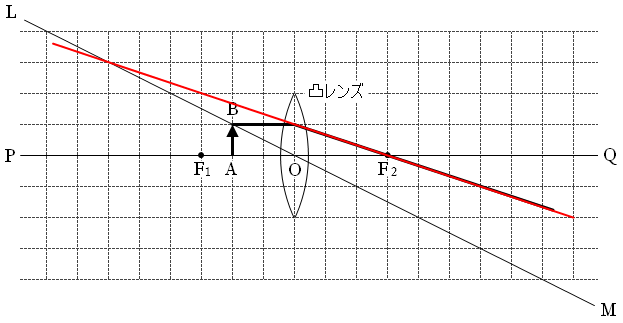
つまりQ側から凸レンズを見ると、物体の先端が下図の赤線上のどこかにあるように感じます。
また、『レンズによる像』の(凸レンズ)の(2)より、凸レンズの中心を通る光線は、そのまま真っ直ぐ進むので、以下のようになり、
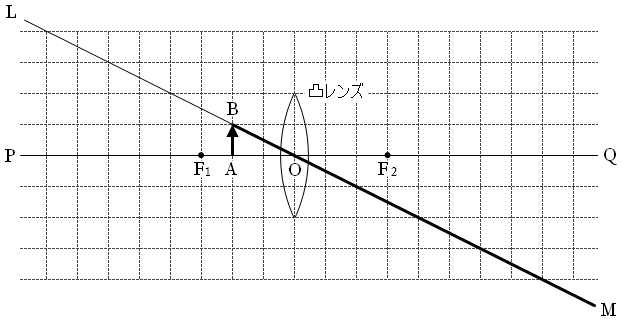
つまりQ側から凸レンズを見ると、物体の先端が下図の青線上のどこかにあるように感じます。
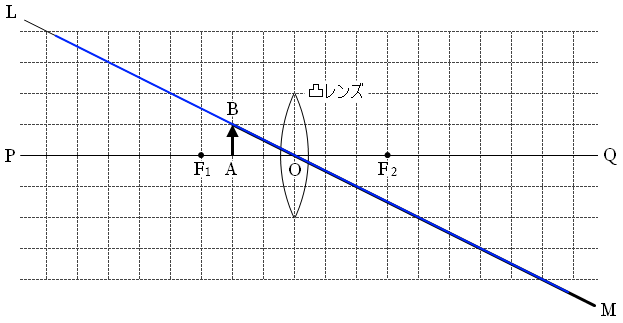
この両方を満たす位置は下図のような位置です。この位置に物体の先端があるように感じるはずです。
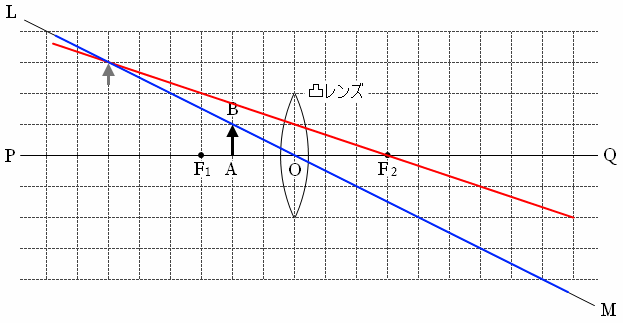
物体の根本の位置は光軸PQ上のままで変わりませんから、虚像は下図のようになります。
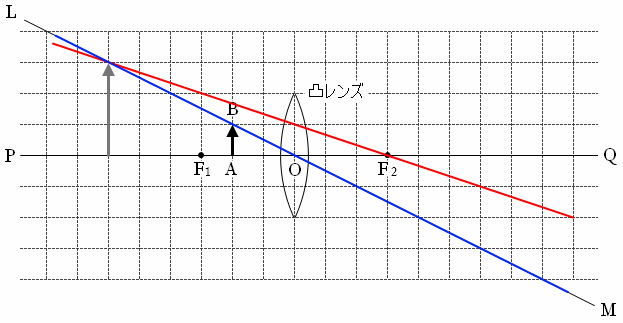
物体の高さと虚像の高さをマス目を見ながら比べると 3 倍になっています。