次の文中の空欄エ・オに入れる数値と語の組合せとして最も適当なものを、下の①~⑧のうちから一つ選べ。
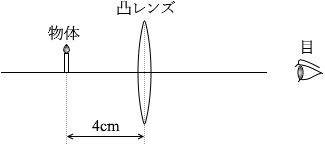
図2のように、焦点距離が 12cm の凸レンズから 4cm の位置に物体を置いたとき、レンズからエcm の位置にオが見えた。
| エ | オ | |
|---|---|---|
| ① | 12 | 実像 |
| ② | 6 | 実像 |
| ③ | 4 | 実像 |
| ④ | 3 | 実像 |
| ⑤ | 12 | 虚像 |
| ⑥ | 6 | 虚像 |
| ⑦ | 4 | 虚像 |
| ⑧ | 3 | 虚像 |
#センター16追試物理
次の文中の空欄エ・オに入れる数値と語の組合せとして最も適当なものを、下の①~⑧のうちから一つ選べ。
図2のように、焦点距離が 12cm の凸レンズから 4cm の位置に物体を置いたとき、レンズからエcm の位置にオが見えた。

| エ | オ | |
|---|---|---|
| ① | 12 | 実像 |
| ② | 6 | 実像 |
| ③ | 4 | 実像 |
| ④ | 3 | 実像 |
| ⑤ | 12 | 虚像 |
| ⑥ | 6 | 虚像 |
| ⑦ | 4 | 虚像 |
| ⑧ | 3 | 虚像 |
#センター16追試物理
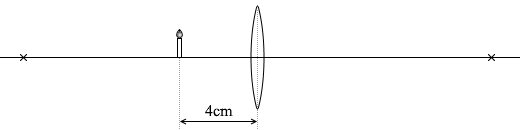 焦点距離が 12cm ということだから、焦点(×)の位置はだいたいこの辺で、
焦点距離が 12cm ということだから、焦点(×)の位置はだいたいこの辺で、
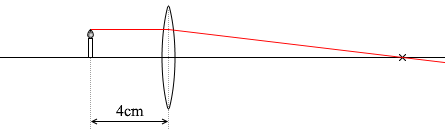 『レンズによる像』で説明した(凸レンズ)の(1)の進み方はこのようになり、
『レンズによる像』で説明した(凸レンズ)の(1)の進み方はこのようになり、
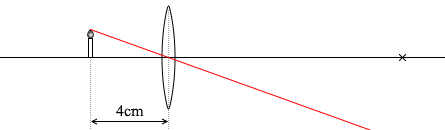 (2)の進み方はこのようになります。
(2)の進み方はこのようになります。
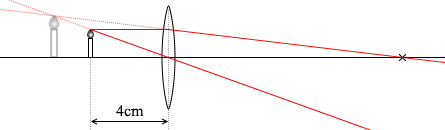 右側からレンズを見たときは、この2つの経路の延長線上に物体の先端があるように(人間の脳内で)感じます。すなわちこのレンズが作る像は実像ではなく虚像です。
右側からレンズを見たときは、この2つの経路の延長線上に物体の先端があるように(人間の脳内で)感じます。すなわちこのレンズが作る像は実像ではなく虚像です。
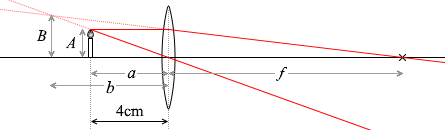 各距離を左図のように定めて、『物体を焦点より近くに置いたとき』で説明したように計算していきますと、
各距離を左図のように定めて、『物体を焦点より近くに置いたとき』で説明したように計算していきますと、
\(\large{\frac{B}{A}}\) = \(\large{\frac{b}{a}}\)
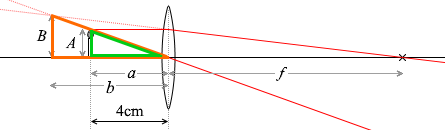
\(\large{\frac{B}{A}}\) = \(\large{\frac{b+f}{f}}\)
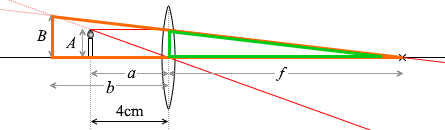
∴ \(\large{\frac{b}{a}}\) = \(\large{\frac{b+f}{f}}\)
⇔ \(\large{\frac{b}{4}}\) = \(\large{\frac{b+12}{12}}\)
∴ 12b = 4b + 48
∴ 8b = 48
∴ b = 6
答えは ⑥ です。
(別解)
レンズの公式(写像公式)に当てはめて解きますと、(b は正の値も負の値もとるものとし、レンズを境に右側を正、左側を負とします)
\(\large{\frac{1}{a}}\) + \(\large{\frac{1}{b}}\) = \(\large{\frac{1}{f}}\)
⇔ \(\large{\frac{1}{4}}\) + \(\large{\frac{1}{b}}\) = \(\large{\frac{1}{12}}\)
∴ \(\large{\frac{b+4}{4b}}\) = \(\large{\frac{1}{12}}\)
∴ 12b + 48 = 4b
∴ 8b = - 48
∴ b = - 6
これは、像ができるのはレンズの左側 6cm の位置ということです。
レンズの公式(写像公式)は正負の扱いがやっかいです。うっかりミスを防ぐためには上で説明したような三角形の相似から答えを導くやり方も覚えておいた方がいいです。
(余談)
本問におけるレンズの倍率は
m = \(\large{\frac{|b|}{a}}\) = \(\large{\frac{6}{4}}\) = 1.5 倍
です。