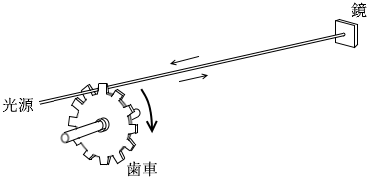
図2のような装置を用いて、光速を測定することができる。最初、歯車が止まっているときには、歯の間を光が通り、遠くにある鏡に反射して再び歯の間を通り抜けてくる。歯車を回転させると、光が反射して戻ってくる間に歯が動いているので、回転数を上げていくと反射光が歯にさえぎられてしだいに暗くなる。さらに回転を速くしていくと再び明るく見えるようになり、最も明るくなるときの回転数から光速が求められる。歯数が 100 の歯車を用いると、回転数が 毎秒300回 になったときはじめて最も明るくなり、光速の値として 3×108m/s が得られた。歯車と鏡の間の距離はいくらか。
#センター06本試
この問題はフィゾーの実験のことであり、その中でも歯と歯の間の部分に戻ってくるまで（明るくなる）とした場合の話です。
光速は c = 3×108 [m/s] であり、 回転数は n' = 300 [回/秒] であり、歯数は N = 100 [個] であるので、求める距離を L [m] としますと、
c = 2L ÷ \(\large{\frac{1}{n'N}}\) = 2n'NL
⇔ 3×108 = 2 × 300 × 100 × L
∴ L = 3×108 × \(\large{\frac{1}{2 × 300 × 100}}\)
= 1×108 × \(\large{\frac{1}{2 × 100 × 100}}\)
= \(\large{\frac{1}{2}}\) × \(\large{\frac{10^8}{100 × 100}}\)
= \(\large{\frac{1}{2}}\) × 104
= 5000 [m]