光速の測定
光の進む速さは有限
日常生活において光の進む速さ（光速=光速度）について意識することはありませんし、光はどんなに離れていても一瞬で伝わる、つまり速さが無限大であるかのように感じてしまいます。しかし17世紀頃には科学者たちは光速が有限であることに気付き始めたようです。ガリレオ・ガリレイ、レーマー、ブラッドリー、フィゾー、フーコー（qGARA）、マイケルソンら様々な科学者が光速の測定を試みました。その中でフィゾーの実験についてはどの教科書にも載っているので本項で解説しておきます。
レーマーの算出
その前にレーマーの算出について触れておきます。
世界で初めて光速の値を示したのは レーマー＊オーレ・クリステンセン・レーマー、17世紀のデンマークの天文学者。イタリアの天文学者ジョヴァンニ・カッシーニの観測データを使って光速度を計算しました。
閉じるといわれています。
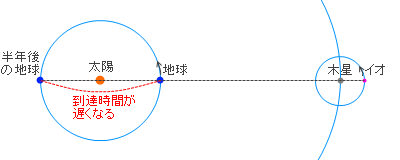木星の周りを回る衛星イオが、地球から見たときに木星の裏側に隠れる、いわゆる”食”の現象が周期的に起こらないことから、光の速さは有限で、地球が太陽の周りを回ってイオから離れる距離の分だけ”食”の現象を伝える光の到達時間が遅くなる、とレーマーは考えました。この仮説により 2.1×108 m/s という光速の値を導き出しました。この値は 299792458 m/s からは大きくズレてますが桁は一応合ってます。実際の計算方法は複雑なのでここでは説明しません。興味のある方は「レーマー 光速」などのキーワードで検索してみてください。
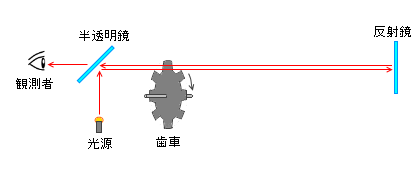フィゾーは左図のような装置を用いました。光源から出た光は半透明鏡で斜めに反射し歯車を通り反射鏡で反射し、再び歯車を通り半透明鏡を通過して観測者に届きます。 
しかし、徐々に歯車の回転を速くしていくと反射した光が歯車の歯に当たり観測者に届かなくなります。歯の隙間から漏れる光が観測者に届くこともあるでしょうが、少なくとも、歯車の回転数を上げていったときに、最も反射光が見えにくくなる瞬間があるはずです。歯車を高速連続シャッターとみなすと、歯車の回転数から高速連続シャッターの開閉の秒数が割り出せます。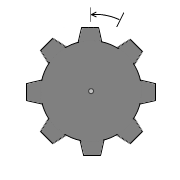
歯の総数を N とすると、光が往って戻って歯に当たるまでに、歯車は1回転のうちの \(\large{\frac{1}{2N}}\) だけ回転します。\(\large{\frac{1}{N}}\) ではありません、\(\large{\frac{1}{2}}\)×\(\large{\frac{1}{N}}\) です。左図では歯の数が８個で、\(\large{\frac{1}{16}}\) だけ回転しています。
勝手な想像ですが、おそらくフィゾーは、最初はこのような装置を作ろうとしたのではないかと思います。ところが長さが足りなくて測定できず（長いのを作ったとしてもねじれてしまって正確な測定はできないでしょうし）、それでいろいろ工夫して、鏡を使った実験装置を考え出したのだと思います。