管楽器は、管の口に息を吹きつけたときに起こる気柱の共鳴を利用して音を出す。共鳴が生じるときの音の振動数について考える。
（問3）次の文章中の空欄ア⋅イに入る数値はいくらか。
図4のように細長い管を用意し、管の一端の近くに振動数 f の音源を置く。音源の振動数 f を 0 から徐々に大きくしていくと、 f = 440 Hz で初めて共鳴が生じた。
次に図5のように同じ管の一端を手で閉じて同様の実験を行う。音源の振動数 f を 0 から徐々に大きくしていくと、アHz に近くなったときに初めて共鳴が生じた。さらに振動数 f を大きくしていくと、イHz に近くなったときにも共鳴が生じた。
（問4）図6のように、問3と同じ細長い管と音源を、ヘリウムガスを満たした十分大きな容器内に入れる。音源の振動数 f を 0 から徐々に大きくしていくとき、初めて共鳴が起こる振動数は 何Hz か。ただし、ヘリウムガス中の音速は、空気中の音速の3倍であるとする。
#センター12本試
（問3）
気温が一定ならば空気中の音速は一定で、波の基本式 v = fλ より、速さが一定であれば振動数の大きさと波長の大きさは反比例するので、音源の振動数を 0 から徐々に大きくしていくということは、大きい波長を徐々に小さくしていくということです。
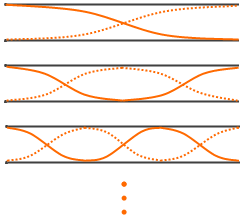『気柱の振動』項で説明したように、開管における定常波で、一番大きいときの波長は、管（気柱）の長さ（ l と置きます）の2倍です。
このときの振動数が f = 440 [Hz] というのであるから、空気中の音速を v と置くと、波の基本式より、
v = 440 × 2l
つまり、管の長さは
l = \(\large{\frac{v}{880}}\)
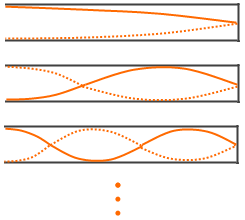閉管における定常波で、一番大きいときの波長は、管の長さの4倍です。つまり、4l = \(\large{\frac{v}{220}}\) です。
このときの振動数を f1 と置きますと、波の基本式より振動数というものは速さを波長で割ったものだから、
f1 = \(\large{\frac{v}{\frac{v}{220}}}\) = 220
アの答えは 220 Hz
二番目に大きいときの波長は、管の長さの \(\large{\frac{4}{3}}\)倍であり、つまり、\(\large{\frac{4}{3}}\)l = \(\large{\frac{4}{3}}\)\(\large{\frac{v}{880}}\) = \(\large{\frac{v}{660}}\) です。
このときの振動数を f2 と置きますと、
f2 = \(\large{\frac{v}{\frac{v}{660}}}\) = 660
イの答えは 660 Hz
（問4）
問3で説明したように、開管における定常波で一番大きいときの波長は、管の長さの2倍であり、つまり、2l = \(\large{\frac{v}{440}}\) です。そして題意よりヘリウムガス中の音速は 3v 。よって、求める振動数を f3 と置くと、波の基本式（v = fλ）の関係より、
3v = f3 × \(\large{\frac{v}{440}}\)
∴ f3 = 132000 [Hz]