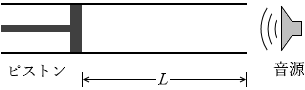
図2のように、ピストンの付いたガラス管の管口付近に音源が置かれている。 管口からピストンまでの距離 L と、音源の振動数 f は連続的に変えられる。音速を 340m/s とし、ガラス管内に定常波（定在波）が発生しているときは、ちようど管口の位置に腹があるとする。
（問3）ピストンを L=50cm の位置で固定し、音源の振動数を f1 としたとき、ガラス管内で共鳴が起こり定常波が生じた。次に、振動数を固定したままピストンをゆっくりと引いて共鳴が起こるかどうか調べたところ、50cm < L < 70cm では共鳴せず、L=70cm の位置で再び共鳴した。f1 は何Hzか。
（問4）次に、ピストンを L=50cm の位置からゆっくりと引きながら、常に共鳴が起きるように音源の振動数を少しずつ変化させた。L=50cm の位置での振動数が f1 、L=70cm の位置での振動数が f2 であったとき、\(\large{\frac{f_2}{f_1}}\) の値はいくらか。
#センター14本試
（問3）
閉管において定常波ができる振動パターンは、
基本振動、
3倍振動、
5倍振動、
7倍振動
…、です。 『気柱の振動』項は、管の長さが一定で波長が変化する場合の話でしたが、本問は、波長が一定で管の長さが変化する場合の話です。
本問では、L が 0.50m から 0.70m までの間では定常波ができなかったということなので、0.50m のときの振動が (2n-1)振動だとすると、0.70m のときの振動はその一つ上の (2n+1)振動ということになります。
（例えば、0.50m のときが基本振動なら 0.70m のときは3倍振動。あるいは、0.50m のときが3倍振動なら 0.70m のときは5倍振動。）
この波の波長
は 0.70 - 0.50 の2倍の 0.40m であり、波の速さが 340m/s であるから、波の基本式（v = fλ）から f1 を求めますと、
f1 = \(\large{\frac{340}{0.40}}\) = \(\large{\frac{3400}{4}}\) = 850 [Hz]
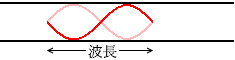
ちなみに、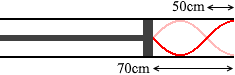
L=50cm のときの振動が5倍振動で、L=70cm のときの振動が7倍振動になっています。
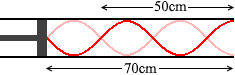
L=50cm のときの振動が基本振動で、L=70cm のときの振動が3倍振動だったりすると、長さのつじつまが合いません。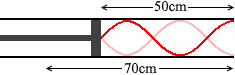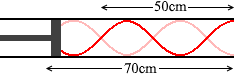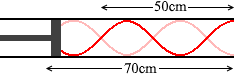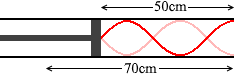
（問4）
「常に共鳴が起きるように音源の振動数を少しずつ変化させた」ということですから、これは
このようなことではなく、
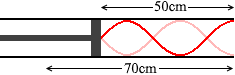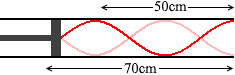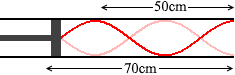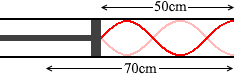このようにしたということです。
波長が\(\large{\frac{7}{5}}\)倍に伸びたということです。（v = fλ より）波の速さが一定のとき、振動数と波長は反比例の関係にあるから、
\(\large{\frac{f_2}{f_1}}\) = \(\large{\frac{5}{7}}\)