気体の共鳴と音速について考える
(問1)次の文章中の空欄5に入れる式として正しいものを、下の①~⑥のうちから一つ選べ。
実験室内に、図1のような一端がピストンで閉じられ、気柱の長さが自由に変えられる管がある。管の開口部でスピーカーから振動数 \(f\) の音を出し、ピストンを開口端から徐々に動かして、最初に共鳴が起こるときの長さを測定すると \(L_1\) であった。さらにピストンを動かし、次に共鳴する長さを測定したところ \(L_2\) であった。これより音速は5と求められる。ただし、開口端補正は無視できるものとする。

① \(fL_2\) ② \(2fL_2\) ③ \(f(L_2 - L_1)\) ④ \(2f(L_2 - L_1)\) ⑤ \(f(L_2 - L_1)\large\frac{L_2}{L_1}\) ⑥ \(f(L_2 - L_1)\large\frac{L_1}{L_2}\)
(問2)次の文章中の空欄6・7に入れる語句として最も適当なものを、それぞれの直後の選択肢のうちから一つずつ選べ。
気柱の長さを \(L_2\) に保ったまま、共鳴が起こらなくなるまで実験室の気温を徐々に下げた。共鳴が起こらなくなったのは、管内の空気の温度が下がったため、管内の6
① 音の波長が長くなった
② 音の波長が短くなった
③ 音の振動数が大きくなった
④ 音の振動数が小さくなった
⑤ 音が縦波から横波になった
からである。
このあと、ピストンの位置を左に動かしていったところ、管の開口端に達するまでに共鳴は7
① 1回
② 2回
③ 3回
④ 0回
起こった。
#共テ21追試物理基礎
 そんな中でピストンが動くわけです。
そんな中でピストンが動くわけです。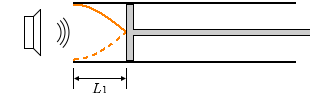 このとき最初に
このとき最初に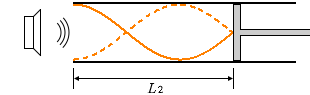 次に共鳴が起こるのは左図のような位置です。
次に共鳴が起こるのは左図のような位置です。 波長が小さくなって共鳴するポイントがピストンの位置とズレてしまったということです。
波長が小さくなって共鳴するポイントがピストンの位置とズレてしまったということです。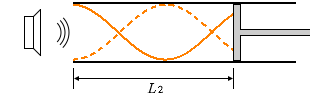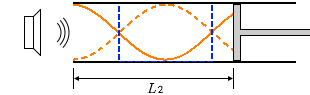 このあと、ピストンを左に動かしていった場合、共鳴するのは ② 2回 です。
このあと、ピストンを左に動かしていった場合、共鳴するのは ② 2回 です。