共振・共鳴

共振

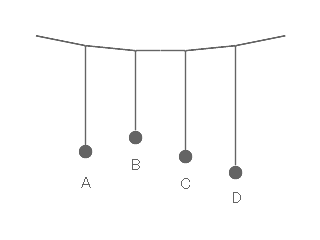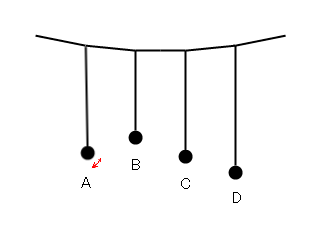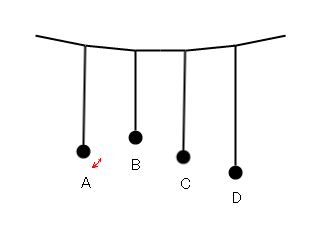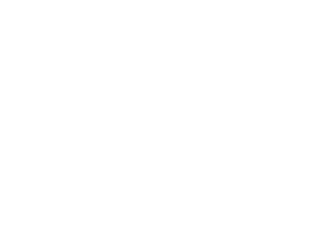左図のように様々な長さの振り子A～Dを吊るし、振り子Aを振動させます。すると、それと同じ長さの振り子Cも徐々に振動を始めます。振り子Cには触ってないにも関わらずです。違う長さの振り子は振動しません。振り子は糸の長さだけで固有振動数が決まるので、振り子Aと振り子Cは固有振動数が同じです。

このように、個々の物体が持つ固有振動数と同じ振動数の揺れを外から加えると物体が振動を始める現象を共振といいます。（電気回路においても共振という現象があります。）

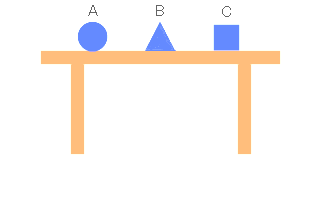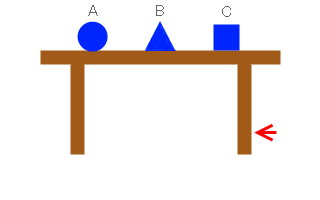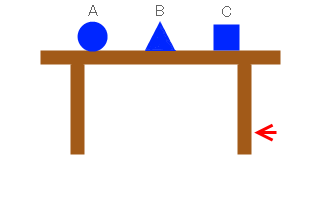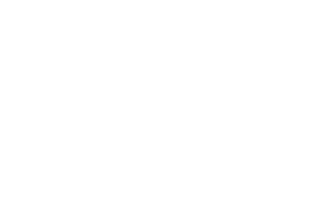例えば、テーブルの上に、100Hz の固有振動数を持つ物体Aと、110Hz の固有振動数を持つ物体Bと、120Hz の固有振動数を持つ物体Cを置き、テーブルの足に 110Hz の振動を与えると、物体Bだけが振動を始めるという超能力ショーのような現象が起こります。

＊ 一般に超高層ビルは地震に強いとされていますが、これは超高層ビルの固有振動数と一般的な地震の振動数が一致しないためです。

しかし、やわらかい地層の平野部で巨大地震が起こると、長周期地震動というものが起こり、超高層ビルの固有振動数と一致して共振を起こしやすく、大変危険であると指摘されています。2003年の十勝沖地震では巨大石油タンクが長周期地震動と共振してしまい、タンクの蓋が破損し大火災を引き起こしました。

巨大な送電線や橋に関しても長周期地震動を考慮して設計する必要があります。

風力発電の風車はタワーやブレードを長くする方が効率は上がりますが、タワーやブレードが作り出す振動はそれらと同じ長さの電線や橋や煙突や避雷針を共振させて不具合を起こしてしまう恐れがあります。
　閉じる

共鳴

共鳴

共振現象の内、音に関するものを共鳴といいます。

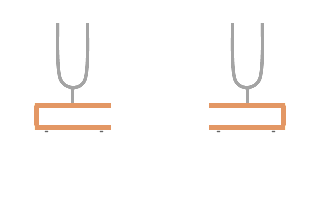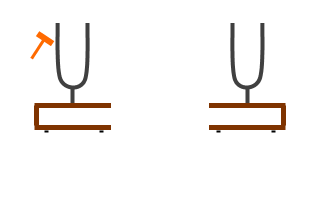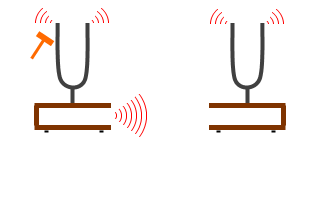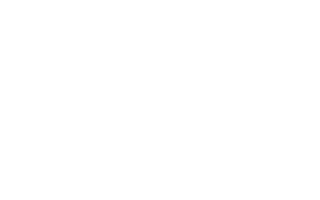同じ固有振動数を持つ共鳴箱付き音叉（おんさ）を２つ用意して、片方を鳴らします。すると、もう片方も鳴り始めます。叩かれた音叉が下の共鳴箱を揺らし、空気を伝わって隣の共鳴箱を揺らし、上の音叉を揺らして鳴らします。

固有振動数が違う音叉同士では共鳴は起こりません。

気柱の共鳴

長さを変えることができる気柱の近くで音叉を鳴らし、気柱の長さを 0 から徐々に長くしていくと、気柱の固有振動数と音叉の固有振動数が一致したところで、気柱は音叉に共鳴して大きく鳴り出します。

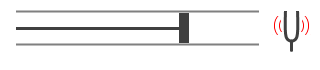さらに気柱を長くしていくと共鳴しなくなり音は止みます。

さらに気柱を長くしていくと再び共鳴が起こります。

１回目に鳴ったときと２回目に鳴ったときの気柱の長さの差から、音叉の発する音の振動数が特定できます。

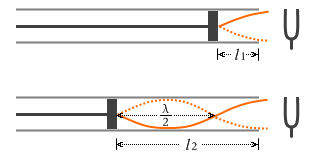このときの波長 λ を求めてみます。

１回目に鳴ったときと２回目に鳴ったときの波の様子は左図のようになっているはずです。

この図から、

　　　　\(\large{\frac{\lambda}{2}}\) = l2 - l1

　　∴　λ = 2(l2 - l1)

ということがわかり、v = f λ という関係式に代入すると（音速を V とします）、

　　　　f = \(\large{\frac{V}{\lambda}}\) = \(\large{\frac{V}{2(l_2-l_1)}}\)

となり、音叉の発する音の振動数がわかります。（開口端補正については今回は無視。＊ 無視するんなら、そもそも λ を割り出すときに l1 を4倍すればいいじゃないか、といわれればその通りです。

で、
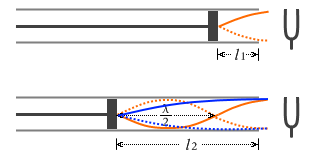気柱の長さを l2 の長さにしたときに、左図の青波のような基本振動が起こっている可能性もあるのですが、これは、先に l1 の長さのときに１回共鳴が起こっているということで、l1 が基本振動で、l2 が3倍振動である、ということがいえて、
これはつまり、l1 を4倍して λ を割り出すんではなく、ちゃんと音が大きくなるポイントを２ヶ所測定して l2 - l1 の長さから λ を割り出すことが大事、ということがいえます。
　 閉じる）

↑ ↓