qO9E6

空気中を伝わる音について、次の問い（問1～6）に答えよ。ただし、風の影響は無視できるものとする。

　

（問1）音の速さに関する次の文章中の空欄ア・イに入れる語と文の組合せとして最も適当なものを、後の①～⑥のうちから一つ選べ。

気温が 0℃ のときと 30℃ のときで、音の速さを比べると、30℃ のときの方がア。また、気温 0℃ と 30℃ で、同じ振動数の音の波長を比べると、イ。

ア イ
① 大きい 30℃ のときの方が長い
② 大きい 30℃ のときの方が短い
③ 大きい 同じ長さである
④ 小さい 30℃ のときの方が長い
⑤ 小さい 30℃ のときの方が短い
⑥ 小さい 同じ長さである

　

　

音の速さを三つの異なる方法で測定した。

　

（問2）1番目の方法として、太鼓とストップウォッチを用いて、次の手順で音の速さを測定した。

太鼓を持ったAさんと、ストップウォッチを持ったBさんが、140m 離れてグラウンドに立っている。Bさんは、Aさんが太鼓をたたくのを見てストップウォッチをスタートさせ、太鼓の音が聞こえたときにストップウォッチを止めた。このとき、ストップウォッチの表示は 0.42s だった。この測定値から音の速さを有効数字2桁で表すとき、次の式中の空欄11～13に入れる数字として最も適当なものを、後の①～⓪のうちから一つずつ選べ。ただし、同じものを繰り返し選んでもよい。

11.12×1013m/s

① 1　② 2　③ 3　④ 4　⑤ 5

⑥ 6　⑦ 7　⑧ 8　⑨ 9　⓪ 0

　

　

（問3）問2で求めた音の速さは、教科書に書かれている式から求めた値よりも小さかった。AさんとBさんは、「その原因は測定時のストップウォッチの操作にある」と考えた。表1に示す、ストップウォッチがスタートした時間とストップした時間の組合せ(a)～(e)から、原因として考えられるものをすべて選び、その記号の組合せとして最も適当なものを、後の①～⓪のうちから一つ選べ。

表 1
ストップウォッチがスタートした時間 ストップウォッチがストップした時間
(a) 太鼓をたたく前 音が届いた後
(b) 太鼓をたたくと同時 音が届く前
(c) 太鼓をたたくと同時 音が届くと同時
(d) 太鼓をたたくと同時 音が届いた後
(e) 太鼓をたたいた後 音が届く前

① (a)と(b)　② (a)と(c)　③ (a)と(d)　④ (a)と(e)　

⑤ (b)と(c)　⑥ (b)と(d)　⑦ (b)と(e)　⑧ (c)と(d)

⑨ (c)と(e)　⓪ (d)と(e)

　

　

（問4）2番目の方法として、「ピッ」という音を一定の間隔で1分間に300回出す装置（電子式メトロノーム）を使い、次の手順で音の速さを測定した。

まず、AさんとBさんは、それぞれメトロノームを持って集まり、その場所で二つのメトロノームから出る「ピッ」という音が同時に聞こえるようにした。次に、一つのメトロノームを持ったAさんが、もう一つのメトロノームを持ってその場にとどまっているBさんから、ゆっくりと遠ざかっていった。すると、Bさんには「ピッ」という音がずれて聞こえるようになった。やがて、AさんがBさんから 70m 離れたときに、再びBさんには二つのメトロノームから出る「ピッ」という音が同時に聞こえた。この結果から求められる音の速さとして最も適当なものを、次の①～⑥のうちから一つ選べ。

① 280m/s　② 300m/s　③ 340m/s

④ 350m/s　⑤ 370m/s　⑥ 420m/s

　

　

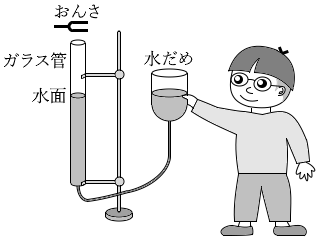
（問5）3番目の方法として、図1のような、水だめを上下させることでガラス管内の空気の部分（以下、これを気柱と呼ぶ）の長さを調節できる装置を用いて、次の手順で音の速さを測定した。

まず、ガラス管の上端の近くまで水面を上げた。次に、ガラス管の上で振動数 500Hz のおんさを鳴らし、水面を下げていき、気柱が共鳴する水面の位置を測定した。このとき、気柱がはじめて共鳴したときの水面の位置と2回目に共鳴したときの水面の位置は 34cm 離れていた。この結果から求められる音波の波長と、音の速さの組合せとして最も適当なものを、後の①～⑧のうちから一つ選べ。

図 1
波長 [m] 音の速さ [m/s]
① 0.17 320
② 0.17 340
③ 0.34 320
④ 0.34 340
⑤ 0.51 320
⑥ 0.51 340
⑦ 0.68 320
⑧ 0.68 340

　

　

（問6）音波の特徴について説明した次の文章中の空欄ウ・エに入れる語と値の組合せとして最も適当なものを、後の①～⑧のうちから一つ選べ。

ヒトの聴くことのできる音の振動数は、およそ 20Hz~20000Hz といわれており、この範囲よりも振動数の大きい音波を超音波という。超音波の波長は、ヒトの聴くことのできる音の波長よりウ。振動数が 34000Hz の超音波の波長は、室温でおよそエである。

ウ エ
① 短い 0.1mm
② 短い 1cm
③ 短い 1m
④ 短い 0.1km
⑤ 長い 0.1mm
⑥ 長い 1cm
⑦ 長い 1m
⑧ 長い 0.1km

#共テ24本試物理基礎

（問1）
『気温によって変化する空気中の音速』で説明したように音速は気温が高いときの方が 大きい です。

また、波の速さは振動数と波長をかけたものだから、振動数が同じで速さが大きい場合、波長は 長い です。

答えは ① です。

　

　

（問2）
0.42s で 140m だったのだから

1.0s では 140×\(\large\frac{1.0}{0.42}\) = \(\large\frac{140}{0.42}\) = \(\large\frac{14000}{42}\) = \(\large\frac{1000}{3}\) ≒ 333.333 ≒ 3.3×102 [m]

答えは 3.3×102m/s であり

11 ③

12 ③

13 ②

　

　

（問3）
3.3×102 という数値が小さくなってしまったのは \(\large\frac{140}{0.42}\) という計算における分母が大きかったからです。計測時間が本来より長くなってしまったということです。そのようになってしまうパターンは ③ (a)と(d) です。

　

　

（問4）
一定の間隔で1分間に300回音が出るということは、音と音の間隔が \(\large\frac{60}{300}\) = \(\large\frac{1}{5}\) = 0.2 [s] ということです。題意よりこの時間の間に音波は 70m 進むということだから 1.0s では 350m 進むことになります。

答えは ④ 350m/s です。

　

　

（問5）
本問では振動数が一定です。また、気温が変化するわけではないので音速も一定です。波の速さは振動数と波長をかけたものだから、波長も一定ということになります。

そんな中で気柱の長さが変わるわけです。 本問の問題設定において、こんな水だめなんかで水面の高さを調整するなんてできないのでは、と思われる方がいるかもしれませんが、水だめがもっと大きくて、ガラス管がもっと小さい場合を想像してみてください。なんとなく調整できそうな気がするんじゃないでしょうか。

このとき最初に共鳴が起こるのは左図のような位置で、

次に共鳴が起こるのは左図のような位置です。

この2つの位置の差が 34cm であり、これは音波の波長の半分であるので、求める音波の波長は倍の 0.68m です。

音の速さはこの波長に振動数 500Hz をかけて、340m/s です。

答えは ⑧ です。

　

　

（問6）
音波は気温が一定なら一定であり、波の速さは振動数と波長をかけたものだから、振動数が大きいということは波長は 短い ということになります。

音の波の速さが 340m/s とすると 34000Hz の振動数の音波の波長は \(\large\frac{340}{34000}\) = \(\large\frac{1}{100}\) [m] となります。

答えは ② です。