次の文章中の空欄ウ・エに入れる数値と語の組合せとして最も適当なものを、後の①~⑧のうちから一つ選べ。
ギターのある弦の基本振動数を 110Hz に調律したい。ここでは、図4のような4倍振動を生じさせ、4倍音を利用して調律を行う。
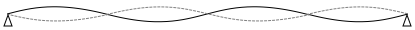
この弦の4倍音(以下、この音をギターの音とよぶ)を鳴らし、おんさの発生する 440Hz の音と比べると、ギターの音の高さの方が少し低かった。また、ギターの音とおんさの音を同時に鳴らすと、1秒あたり2回のうなりが聞こえた。このとき、ギターの音の振動数はウHz である。
次に、1秒あたりのうなりの回数が減っていくように弦の張力を調節する。弦の張力の大きさが大きいほど、弦を伝わる波の速さは大きくなるので、弦の張力の大きさを少しずつエしていけばよい。うなりが聞こえなくなったとき、ギターの音とおんさの音の振動数が一致し、この弦の基本振動数は 110Hz になる。
| ウ | エ | |
|---|---|---|
| ① | 432 | 小さく |
| ② | 432 | 大きく |
| ③ | 438 | 小さく |
| ④ | 438 | 大きく |
| ⑤ | 442 | 小さく |
| ⑥ | 442 | 大きく |
| ⑦ | 448 | 小さく |
| ⑧ | 448 | 大きく |
#共テ23本試物理基礎