振動数がわずかに異なる2つの音を同時に鳴らすと「ゥワーン、ゥワーン」と音が大きくなったり小さくなったりする不思議な現象が起こります。この現象をうなりといいます。お寺の鐘の音もよく聞くとうなりが感じられます 梵鐘の形状がわずかに歪んでいることから、複数の音が発せられ、それらがうなりを生むらしいです。 。 蛍光灯の下の扇風機や、TVに映るプロペラ等のワゴンホイール効果 Wikipediaも同じ原理です。
たとえば、440Hz の音と 444Hz の音を鳴らすと、2つの音の中間の高さの音が 4Hz の振動で大きくなったり小さくなったりします。うなりが発生する原理は数学的に説明することができます 以下で、図形的に説明します。補足ページで数式的に説明します。 。
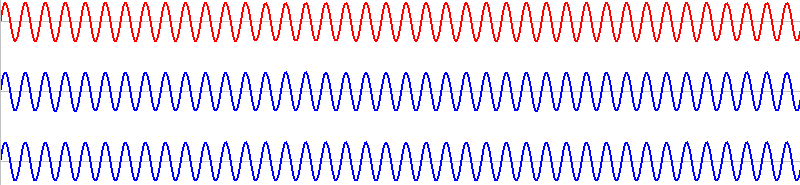
このような波形の音があるとします。横軸は時間です 横軸を変位と考えることもできなくはないです。ある瞬間を切り取ったときの、音源からの距離を横軸とする考え方です。 。振動数を \(f_1\) [Hz] とします。
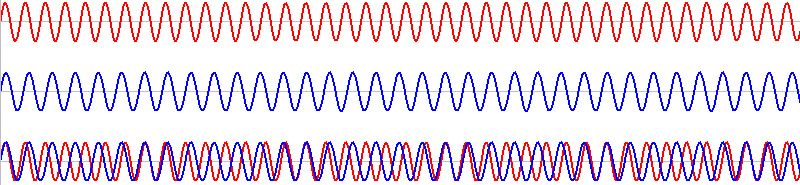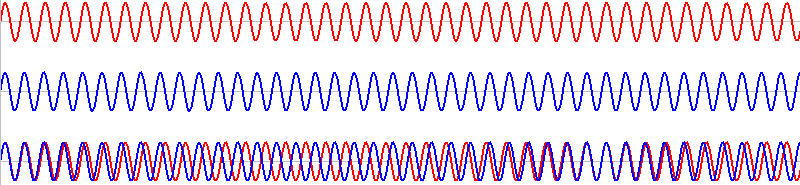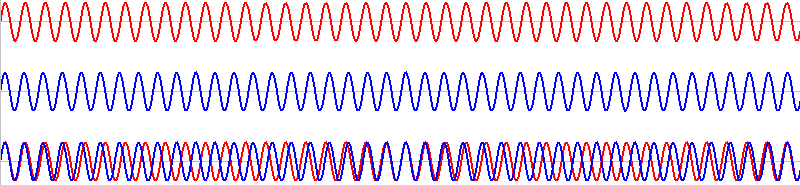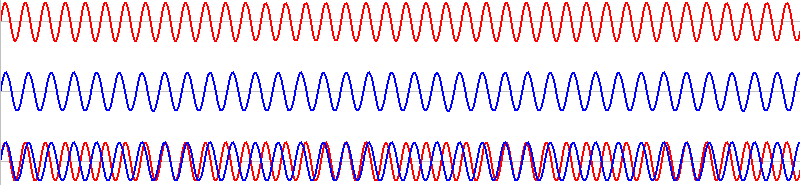
振動数がわずかに異なる音というのは、元の音の波形をわずかに引き伸ばすか縮めるかしたような波形の音です。青波の振動数を \(f_2\) [Hz] とします。
全コマ表示してみます。
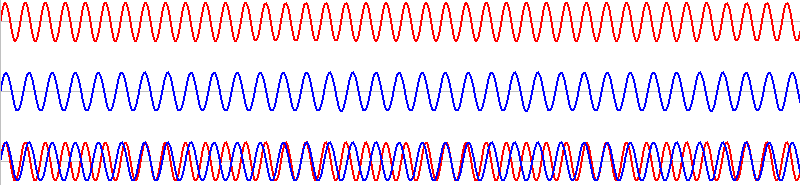
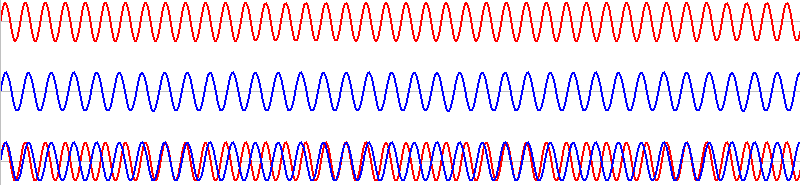
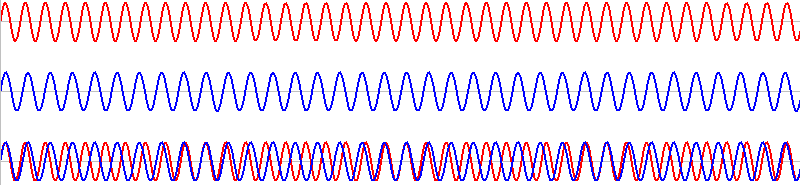
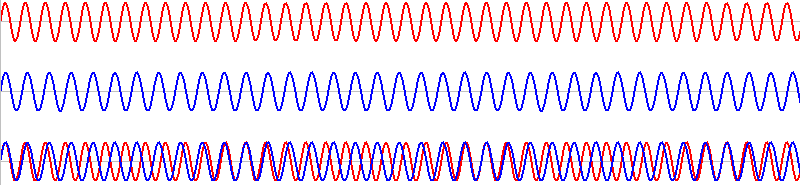
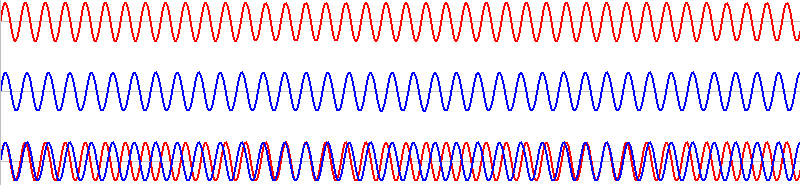
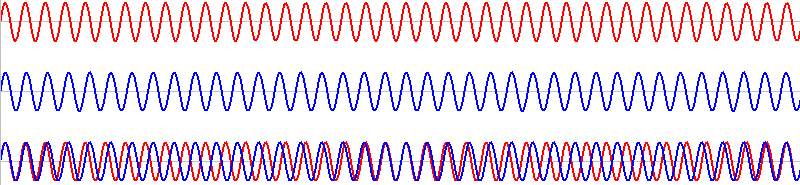
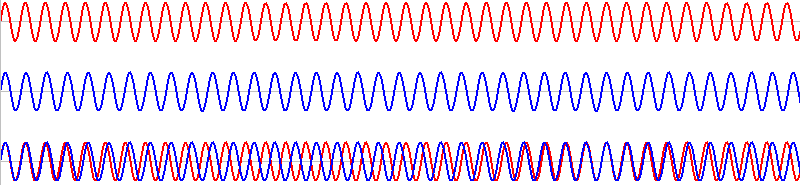
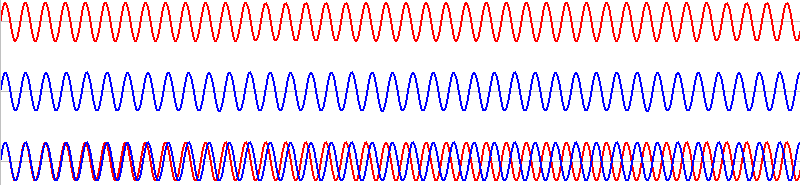
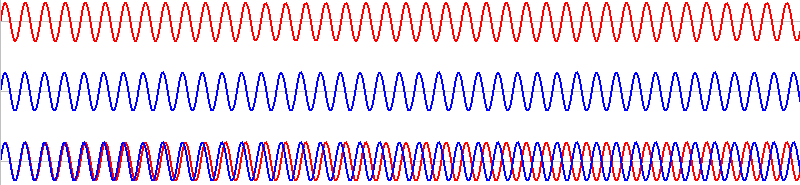
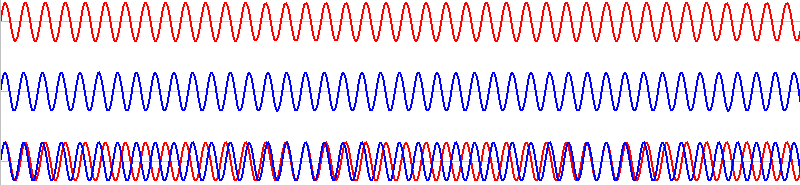
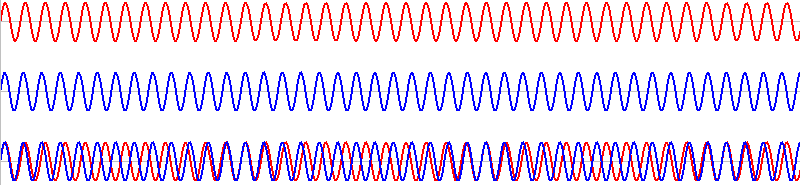
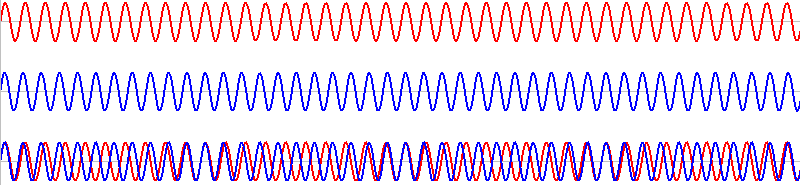
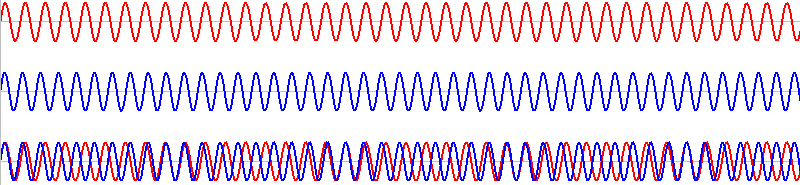
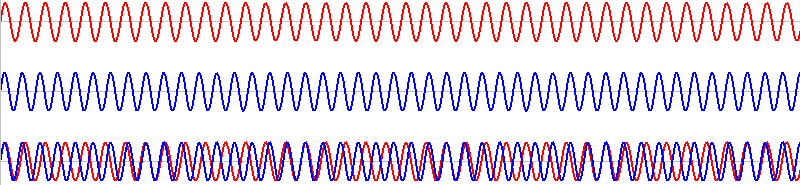
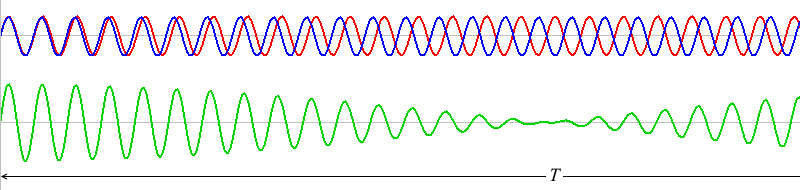
このような2つの音を同時に鳴らすと、その波形は重ね合わされ（足し合わされ）、
このようになります。
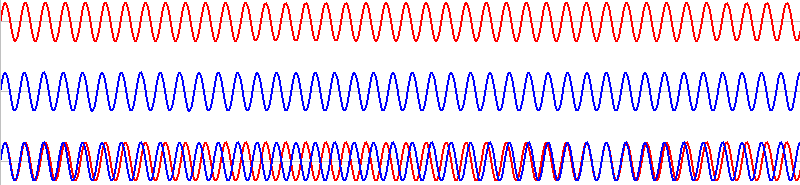
赤波と青波の振動数の差が大きいとき、
緑波はこのようになってしまいます。ここまで崩れるとうなりとは呼びません。うなりは振動数の差が小さい波同士でないと形成されません。
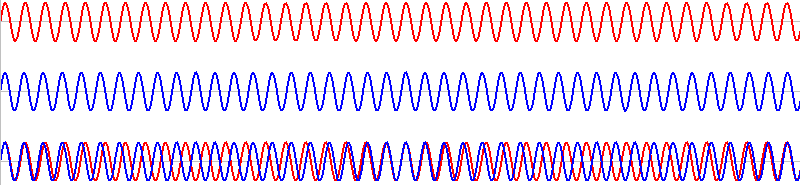
細かい振動と大きい振動がありますが、大きい方がうなりです。このうなりの振動数を \(f\) [Hz] 、周期を \(T\) [s] とします。
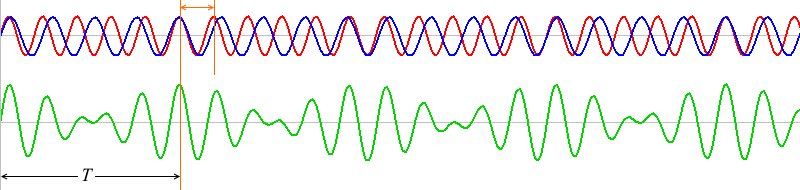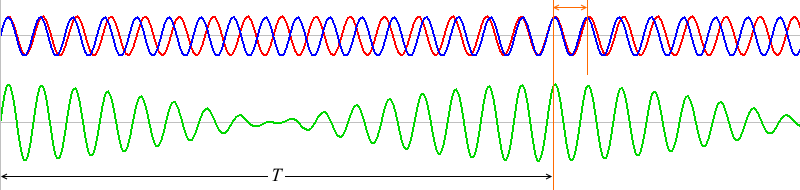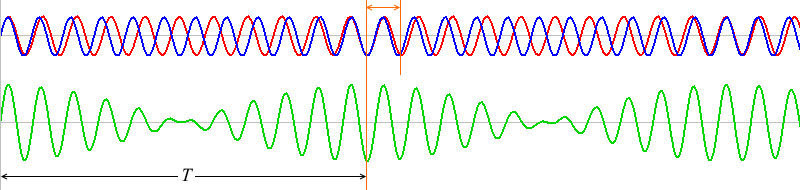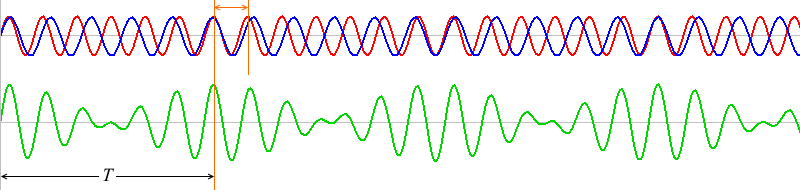
\(T\) の部分の赤波と青波はちょうど1波長分ズレています。
全コマ表示してみます。
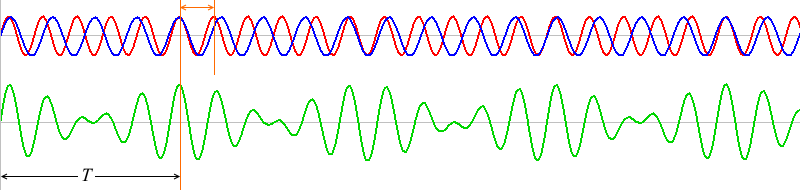
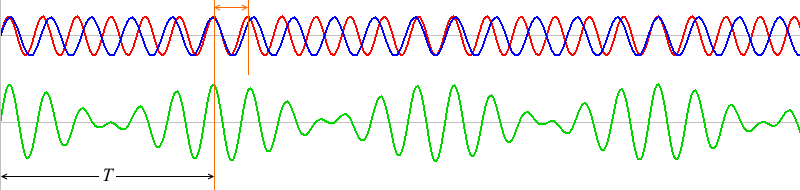
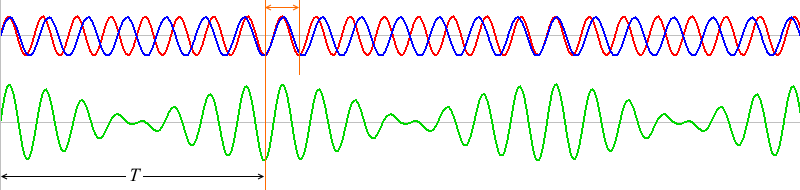
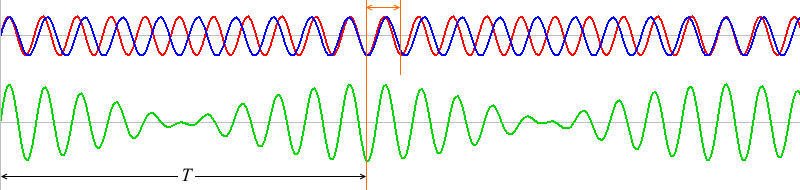
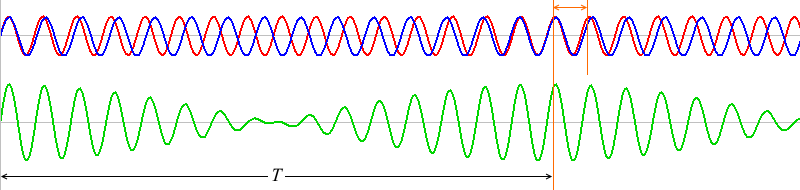
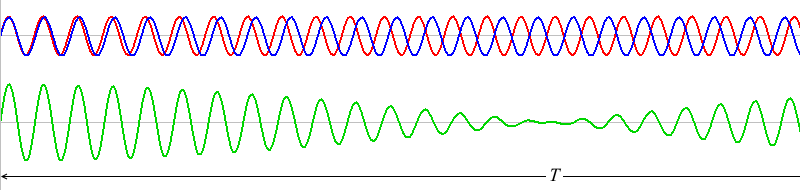
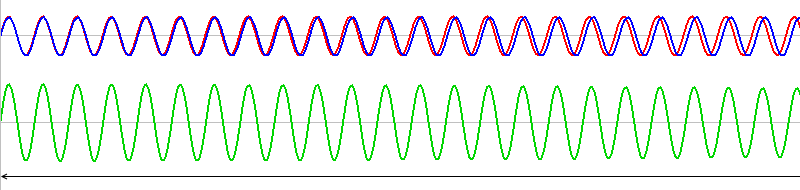
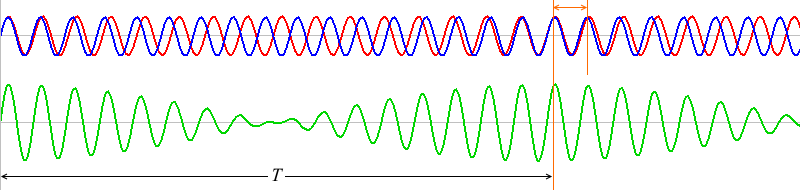
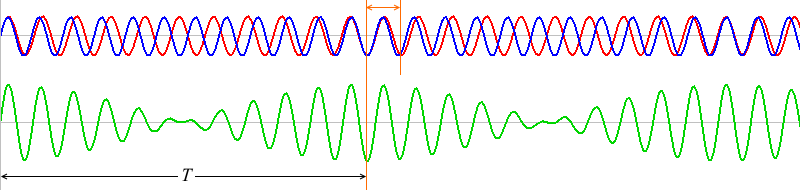
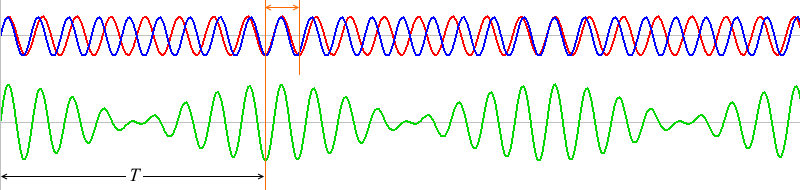
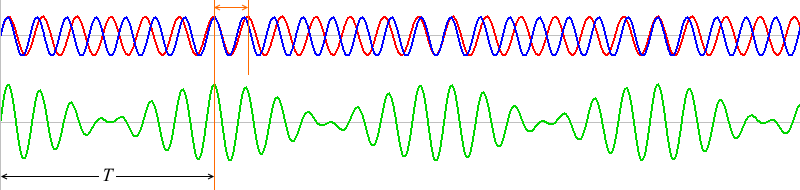
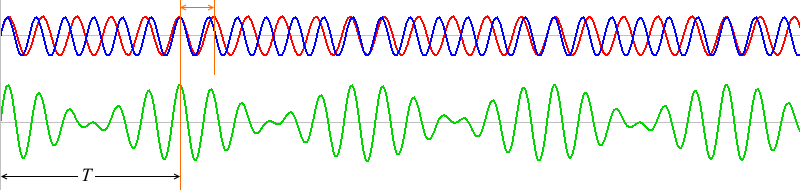
1波長分ズレたものが何回も繰り返しています。ちょうど1波長ズレた波同士は、\(T\) だけ経つと再び出会うことができます。
それ以外の箇所を区切りとすると繰り返しが成立しません。
2波長分ズレた箇所（上図では10と12）には、よく見るとその半分の位置に区切り箇所（5と6）があるはずです。
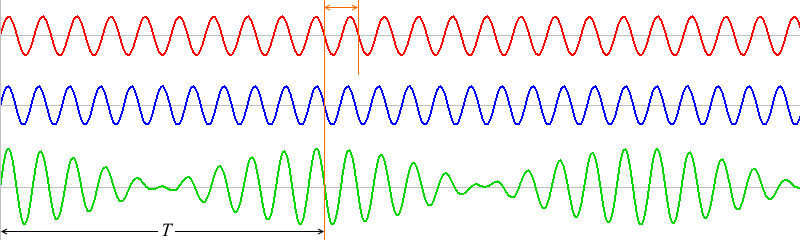
というわけで、\(T\) の区間の赤波と青波の波の個数は1個分、差があります。
\(T\) 間の赤波の個数は（振動数×周期） \(f_1T\) 個で、青波の個数は \(f_2T\) 個です。これの差が1個なので、
\(| f_1T - f_2T | = 1\)
です。つまり、
\(| f_1 - f_2 | = {\large\frac{1}{T}}\)
です。そして \(f = {\large\frac{1}{T}}\) であるので以下のことがいえます。
うなりの振動数
\(\boldsymbol{f = | f_1 - f_2 |}\)
これは、差が同じならばうなりの振動数が同じということです。たとえば、
22.2Hz の波と 24.3Hz の波が作るうなりと、
31.3Hz の波と 33.4Hz の波が作るうなりは、振動数が同じ（どちらも 2.1Hz）です。
33.4Hz の波と 31.3Hz の波が作るうなりと、33.4Hz の波と 35.5Hz の波が作るうなりも同じ（2.1Hz）です。
振動数 20Hz の波というものは1秒間に20回振動するわけですから、\(t\)=0 から \(t\)=1 の間に20個の波があるということです。これをグラフにしますと、
このようになりますが、この波に様々な振動数の波を当てると、うなりの波形は、
このように変化します。
全コマ表示してみます。
閉じる
このとき、\(t\)=1 の付近の波形をよく見ますと、ズレた波の個数分がうなりの振動数になっています。
赤波と青波が1個分ズレたときのうなりの波形。1秒間に1個。
赤波と青波が2個分ズレたときのうなりの波形。1秒間に2個。
赤波と青波が2.5個分ズレたときのうなりの波形。1秒間に2.5個。
このことがまさに \(f = | f_1 - f_2 |\) の意味です。拡大鏡のようです（『モアレ』項参照）。
また、\(t\)=\(T\) の付近をよく見てみますと、
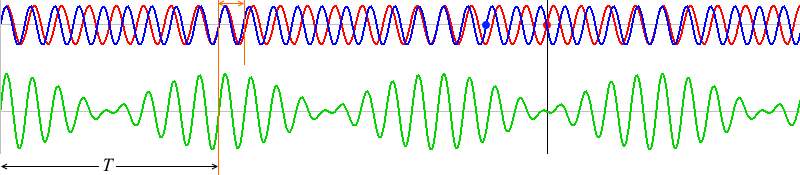
上で説明したように、赤波と青波がちょうど波1個分ズレています。ちなみにこのとき、\(T\) が2.5回繰り返されて1秒になるので \(T\) = 0.4s です。