キルヒホッフの法則
キルヒホッフの第1法則
キルヒホッフの第1法則
電気回路の任意の分岐点について、そこに流れ込む電流の和は、そこから流れ出る電流の和に等しい。
「任意の分岐点について」の意味は「どの分岐点においても、その分岐点に着目したときに」という意味です。
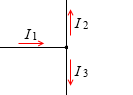この法則は、左図のような回路において I1 = I2 + I3 であること（中学理科で習ったこと）を一般化（拡張）したものです。電流が回路の途中で増えたり減ったりしてしまってはおかしいので、当たり前といえば当たり前です。
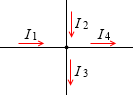左図のように４つに分岐していて電流の方向が分かっている場合、I1 + I2 = I3 + I4 という式が立てられます。
この式は I1 + I2 - ( I3 + I4 ) = 0 とも書けます。
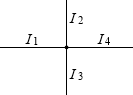電流の方向が分かっていない場合なら、I1 + I2 + I3 + I4 = 0 という式を立てて、流れ込む方向が正、と決めて（あるいは流れ出る方向が正と決めて）、各量は正の値だけでなく負の値も取りうるとすればいいです。
でも、I1 、I2 、I3 、I4 のすべてが正、あるいはすべてが負、ということはありえません。
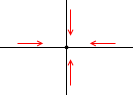すべての電流が流れ込む方向だったり、
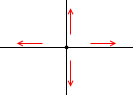すべての電流が流れ出る方向だったりすることはありえないからです。
キルヒホッフの第1法則は水道管や道路交通においても成り立っています。ある領域に着目したときに、流れ込む量と流れ出る量は同じになっています。
キルヒホッフの第2法則
キルヒホッフの第2法則
電気回路の任意の一回りの閉じた経路について、電位差の和は 0 である。
「電位差の和は 0 である」の部分は「起電力の和は、電圧降下の和に等しい」と書き換えることもできます。電圧降下というのは抵抗によって下がった電圧のことです。電位差というのは電位の差のことであり電圧のことです。
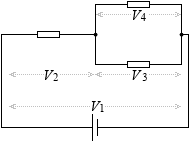この法則は、左図のような回路において、V3 = V4 であったり、V1 = V2 + V3 であること（中学理科で習ったこと）を一般化（拡張）したものです。
ある地点から出発して電位が上がったり下がったりしながら一周して元の位置に戻ってくると電位はスタートしたときと同じである、という当たり前のことです。
キルヒホッフの第2法則は登山においても成り立っています。どんな登山ルートを辿ろうとも、出発地点に戻ってくれば標高は元通りです。
経路その1
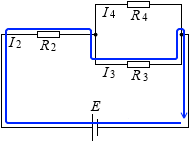左図の青色の経路において、右回りを正とします。起電力を E とします。
すると、この起電力は、図において左向き、経路において右回りに電流を流そうとし、電位を上昇させようとするから、正、つまり + E 。
次に、R2 は電位を降下させようとするから、負で、- R2I2 ＊（電位差）=（電圧）=（抵抗）×（電流）です。オームの法則です。
閉じる。
次に、R3 も電位を降下させようするから、負で、- R3I3 。
つまり、
+ E - R2I2 - R3I3 = 0 ……①
となるわけです。
このとき、キルヒホッフの第2法則の「電位差の和は 0 である」の部分を「起電力の和=電圧降下の和」と覚えた場合は、
（右回りを正として）起電力は電流の向きと同じなので、正で、E 。
次に、R2 は電流の向きと経路の向きが同じで、抵抗は電位を「降下」させ、その分量は R2I2 ＊このときもし電流の向きが右回りと逆だったら（左回りだったら）、R2 は「右回りには電位を降下させない（むしろ上昇させる）」と考えて、- R2I2 とします。
閉じる。
次に、R3 も同様に R3I3 。
つまり、
E = R2I2 + R3I3 ……②
となります。
もし、（右回りでなく左回りを正）と決め、「電位差の和は 0 である」方式を採用すると、
- E + R2I2 + R3I3 = 0 ……③
という式が立てられますが、
これら３つの式をよく見ると、②式は①式を移項しただけ、③式は①式の両辺に - を掛けただけであり、３つの式はまったく同等の式であると分かります。どのような考え方で式を立てても結局は同じになります。しかし、正負の見極めがややこしいのでうっかりミスが起きやすいです。
経路その2
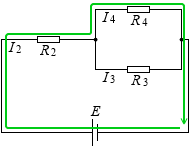左図の緑色の経路に関しては、右回りを正としますと、キルヒホッフ第2法則の式は、
+ E - R2I2 - R4I4 = 0
となります。
経路その3
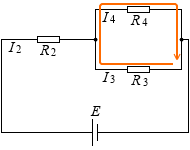左図のオレンジ色の経路に関しても、キルヒホッフの第2法則の式を立てることができます。右回りを正とします。すると、この経路には起電力は無く、I3 の向きは右向きなので、
R3I3 - R4I4 = 0
となります。（ I3 が右向きなので、R3 を左向きに通過する場合に、電位は上がるので、第一項は -R3I3 ではなく R3I3 。電流は電位の高い所から低い所に流れます。）
イメージ図
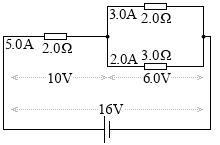電気回路における電流や電位差の大きさはイメージしにくいものですが、
電流のイメージ図
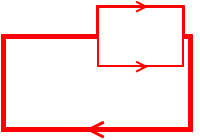電流の大きさを、線分の太さとして図を描くと、電流の様子がイメージしやすくなります。
枝分かれした支流の太さの合計は、元の電流の太さです。
キルヒホッフの第1法則を表現しています。
電位差のイメージ図
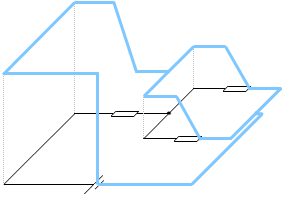また、電位を水位に例えて図を描くと、電位差の様子がイメージしやすくなります。
起電力は水を垂直に汲み上げるポンプに例えることができます。抵抗は水位を下げる装置とみなすことができます。
キルヒホッフの第2法則を表現しています。ある地点からスタートして１周して同じ場所に戻ってくると、電位は元と同じです。
例題
キルヒホッフの法則に関する問題は慣れるまではややこしくて間違いやすいので、例題を使って説明してみます。
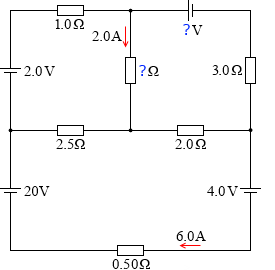左図の ？[V] 、？[Ω] の大きさと、各抵抗を流れる電流の向きと大きさを求めよ、という問題が出題されたと仮定して、これを解いてみます。
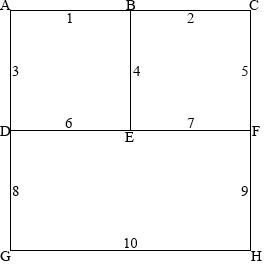角と辺に符号を振り、各位置の装置の目安とします。
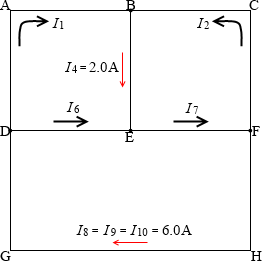まず、左図のように電流の向きを仮設定します。（後で向きを訂正します）
このとき、I1 = I3 、I2 = I5 、I8 = I9 = I10 です。電流にしてみれば、左図の電気回路の辺の数は１０個でなく６個です。分岐点の数が４個で、１つの分岐点から３つの枝が出ていて、１つの辺には２つの端が付いている、ことからすると、辺の数は、4 × 3 ÷ 2 = 6 です。
キルヒホッフの第1法則の式
キルヒホッフの第1法則の式を立てます。（A はアンペアです）
（分岐点Bについて） I1 + I2 = 2.0A ……ⓐ
（分岐点Dについて） 6.0A = I1 + I6 ……ⓑ
（分岐点Eについて） 2.0A + I6 = I7 ……ⓒ
（分岐点Fについて） I7 = I2 + 6.0A ……ⓓ
なのですが、４つの式のうち１つは必要ありません。
ⓐ式を変形して - I1 = I2 - 2.0A
ⓑ式を変形して I1 + I6 = 6.0A
ⓒ式を変形して I7 - I6 = 2.0A
３式を足し合わせると I7 = I2 + 6.0A となり、ⓓ式が導かれます。
４つの式のうち３つを用いると必ず残りの１式が導かれます。事実上、方程式は３個、です。
分岐点が１２個なら方程式は１１個です。
最後の１個の分岐点の状態は、それ以外の１１個の分岐点の状態によって決定づけられてしまうのです。
キルヒホッフの第2法則の式
次に、キルヒホッフの第2法則の式を立ててみます。
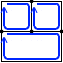考えうる経路の数は左図の３個です。
向きは右回りでも左回りでも構いませんが、今回は右回り、と決めます。
左図のような電気回路では４個です。
面の数だけ経路があり、その数だけ方程式が立てられます。
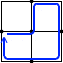このような経路を考えて方程式を立ててもいいのですが、これは 
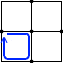と 
と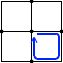 
を足し合わせただけのものです。あるいは、 
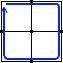から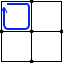 
を引いただけのものです。ですから独立した経路とはみなされません。計算ミスを犯すもととなりますからあまり複雑な経路は考えない方がいいです。
経路の数は面の数です。今のこの問題では３個です。
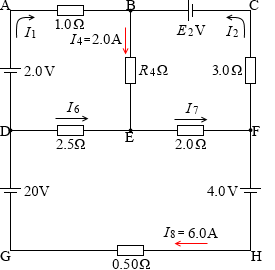？[V] を E2 [V] 、？[Ω] を R4 [Ω] と置きます。
「起電力の和=電圧降下の和」方式でなく、「電位差の和は 0 である」方式で式を立てます。
（経路A→B→E→D→Aについて）
（A→B）電流はA→Bに流れていて、抵抗を通過すると電位が下がるので、
- 1.0Ω×I1 （もし真の電流の向きが仮設定と逆であった場合は I1 の値が負となり、- 1.0Ω×I1 の値は正となり、A点よりB点の方が電位が高いことになります。）
（B→E）電流はB→Eに流れていて、抵抗を通過すると電位が下がるので、
- R4×2.0A
（E→D）電流はD→Eに流れていて、電位はD点の方が高いので、E点からD点を見ると電位が高くなっているので、
+ 2.5Ω×I6
（D→A）起電力はD→Aの方向に向いているので、D点からA点を見ると電位が高くなっているので、
+ 2.0V
つまり、
- 1.0Ω×I1 - R4×2.0A + 2.5Ω×I6 + 2.0V = 0 ……ⓔ
（経路B→C→F→E→Bについて）
（B→C）起電力の向きがB点の方向を向いているのでC点の方が電位が低く、（起電力については電流の方向と無関係で、起電力の向く方向が必ず電位が高くなります。）
- E2
（C→F）電流はF→Cに流れていて、電位はF点の方が高いので、C点からF点を見ると電位が高くなっているので、
+ 3.0Ω×I2
（F→E）電流はE→Fに流れていて、電位はE点の方が高いので、F点からE点を見ると電位が高くなっているので、
+ 2.0Ω×I7
（E→B）電流はB→Eに流れていて、電位はB点の方が高いので、E点からB点を見ると電位が高くなっているので、
+ R4×2.0A
つまり、
- E2 + 3.0Ω×I2 + 2.0Ω×I7 + R4×2.0A = 0 ……ⓕ
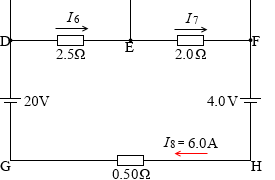
（経路D→E→F→H→G→Dについて）
（D→E）電流はD→Eに流れていて、抵抗を通過すると電位が下がるので、
- 2.5Ω×I6
（E→F）電流はE→Fに流れていて、抵抗を通過すると電位が下がるので、
- 2.0Ω×I7
（F→H）起電力の向きがF点の方向を向いているのでH点の方が電位が低く、
- 4.0V
（H→G）電流はH→Gに流れていて、抵抗を通過すると電位が下がるので、
- 0.50Ω×6.0A
（G→D）起電力はG→Dの方向に向いているので、G点からD点を見ると電位が高くなっているので、
+ 20V
つまり、
- 2.5Ω×I6 - 2.0Ω×I7 - 4.0V - 0.50Ω×6.0A + 20V = 0 ……ⓖ
方程式の数と未知数の数
これで方程式が ⓐ式、ⓑ式、ⓒ式、ⓔ式、ⓕ式、ⓖ式、と６個そろいました。求めたい未知数は E2 、R4 、I1 、I2 、I6 、I7 の６個です。方程式が未知数と同じ個数あるので、解が求められるはずです。未知数が n 個のときは方程式が n 個あれば解が求まります。
解を求める
各方程式を書き直します。
I1 + I2 = 2.0 ……ⓐ
6.0 = I1 + I6 ……ⓑ
2.0 + I6 = I7 ……ⓒ
- I1 - 2.0R4 + 2.5I6 + 2.0 = 0 ……ⓔ
- E2 + 3.0I2 + 2.0I7 + 2.0R4 = 0 ……ⓕ
- 2.5I6 - 2.0I7 - 4.0 - 3.0 + 20 = 0 ……ⓖ
ⓒ式をⓖ式に代入して、
- 2.5I6 - 2.0×(2.0 + I6) + 13 = 0
- 2.5I6 - 4.0 - 2.0I6 + 13 = 0
- 4.5I6 = - 9.0
I6 = 2.0
これをⓑ式、ⓒ式に代入して、
I1 = 4.0
I7 = 4.0
ⓐ式に代入して、
I2 = - 2.0
これらをⓔ式に代入して、
- 4.0 - 2.0R4 + 2.5×2.0 + 2.0 = 0
- 2.0R4 = - 3.0
R4 = 1.5
ⓕ式に代入して、
- E2 + 3.0×(-2.0) + 2.0×4.0 + 2.0×1.5 = 0
- E2 + 5.0 = 0
E2 = 5.0
これですべての未知数が判明しました。I2 は負の値になりましたので、仮設定とは逆向きということです。
すべての数値を電気回路図に書き込んでみます。
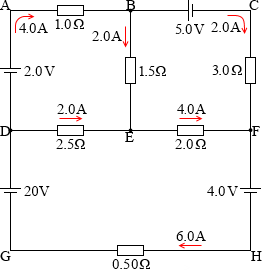
検算
G点の電位を 0V としてA点～H点までの電位を記入して、矛盾がないか検算してみます。
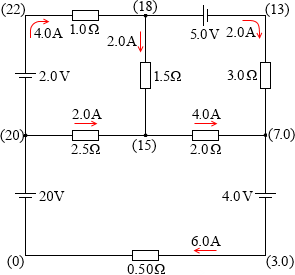起電力の向き、電流の向きに矛盾は無さそうです。
電流と電位差のイメージ図
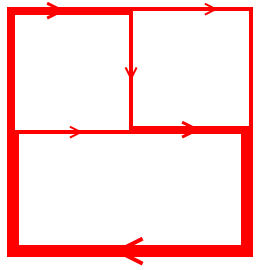電流のイメージ図
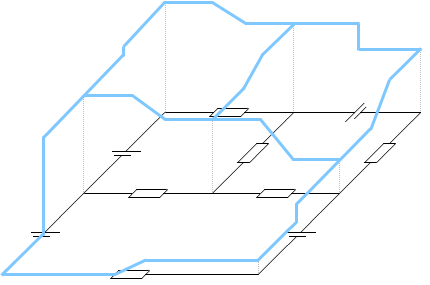電位差のイメージ図
電流と逆向きの起電力
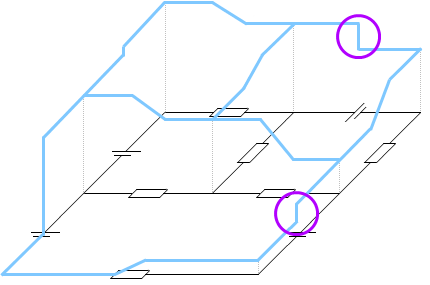上の例題における左図の２箇所の起電力については、電流の向きと起電力の向きが逆です。
上の方で起電力は汲み上げポンプに例えられると説明しましたが、この場合でも起電力は電流の流れに逆らいながら汲み上げポンプのような力を発揮しています。ただ、電流の流れに負けているのです。
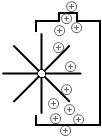起電力が左図のような電池だとすれば、上から電荷が勢い良く降りてくるのに逆らって上に引き上げようと頑張っているけれども結局電荷の勢いに負けて回転翼は右回りに回転してしまっている状態です。しかし電荷の勢い（=電圧）は弱めています。その分、電位が下がっているわけです。
これが充電式電池であれば、充電されている状態です。ゼンマイに例えれば、ゼンマイが巻き上げられている状態です。