コイルを流れる交流
コイルとコンデンサーと直流と交流
『自己誘導』項では、コイルに直流を流した場合について、
『コンデンサーを含む直流回路』項では、コンデンサーに直流を流した場合について説明しました。
本項では、コイルに交流を流した場合について、
『コンデンサーを流れる交流』項では、コンデンサーに交流を流した場合について説明します。
交流の場合は独特の変化の仕方をします。
交流電源とコイルを接続した回路
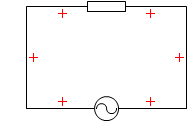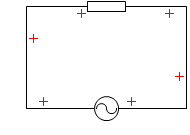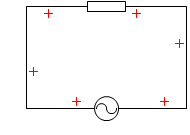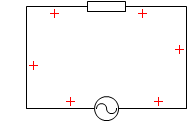
 交流電源と抵抗を接続した単純な回路について、電荷の動きの様子を表すと、
交流電源と抵抗を接続した単純な回路について、電荷の動きの様子を表すと、
 このようになりますが(動きをゆっくりと表しました)、
このようになりますが(動きをゆっくりと表しました)、
交流電源  を
を  このように表し、電荷の動きを
このように表し、電荷の動きを  このように表しますと、
このように表しますと、
 回路の様子はこのようになります。電圧と電流の位相(タイミング)が一致しています。
回路の様子はこのようになります。電圧と電流の位相(タイミング)が一致しています。
ところが、抵抗ではなくコイルを接続した回路では様子が違ってきます。
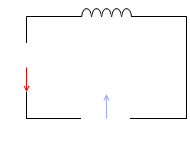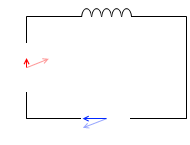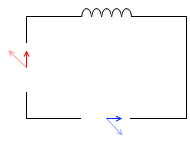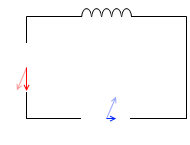 電流の位相が電圧に比べて遅れます。コイルで自己誘導が起こり、電流の増減の変化を邪魔するからです。
電流の位相が電圧に比べて遅れます。コイルで自己誘導が起こり、電流の増減の変化を邪魔するからです。
抵抗が接続されている場合ならば、電圧を大きくしていけばそれに伴って電流も大きくなっていきますが、コイルが接続されている場合は、電圧を大きくしていき電流も大きくなっていくと、その変化量が大きいときほど邪魔され、変化量が落ち着いた瞬間に邪魔は無くなりもっとも多くの電流が流れます。
おもちゃの"指ハブ"のようなイメージです。『振動回路』項もご参照ください。
電流を表す式を求める
交流電源の電圧を V = V0sinωt [V](V0 は最大値)、回路を流れる電流を I [A] 、コイルの自己インダクタンスを L [H] としますと、コイルに発生する自己誘導起電力 VL [V] は、
VL = - L\(\large{\frac{ΔI}{Δt}}\)
です。そして、回路に電流が流れるということは一周して戻ってくると電位が元通りになる*キルヒホッフの第2法則のことです。
右回りを正の方向として式を立てると、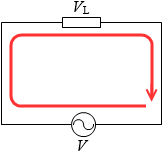
V + VL = 0
⇒ V - L\(\large{\frac{ΔI}{Δt}}\) = 0
です。
これは、「並列接続では電圧が同じ」という中学理科で習ったことを難しく言い換えただけのものです。
あと、ことわっておきたいのが、VL は能動的な起電力ではなく、受動的な起電力であるということです。
V が存在して初めて VL が存在します。V と VL には、ごくごくごくごくわずかなタイムラグが発生します。光の速度のタイムラグです。電圧と電流のタイミングのズレが 90° だとすれば、V と VL はたとえば 0.001° とか 0.0001° とかあるいはもっともっと小さいズレが生じます。V と VL は完全に同時に発生するものではありません。完全に同時に発生するとなると電荷は移動しません。
 西から5N、東から5N、同時に押されたら、ばねは動きません。
西から5N、東から5N、同時に押されたら、ばねは動きません。
 西が壁で、東から5Nで押されたら、その後、ばねは西から5Nで跳ね返されて、東に向かって動きます。
西が壁で、東から5Nで押されたら、その後、ばねは西から5Nで跳ね返されて、東に向かって動きます。
閉じるということですから、
V + VL = 0
⇒ V - L\(\large{\frac{ΔI}{Δt}}\) = 0
∴ V = L\(\large{\frac{ΔI}{Δt}}\)
∴ \(\large{\frac{ΔI}{Δt}}\) = \(\large{\frac{V}{L}}\)
= \(\large{\frac{V_0\sinωt}{L}}\)
この式の右辺は、電流 I を時間 t で微分するという意味です。それが \(\large{\frac{V_0\sinωt}{L}}\) になるということです。
両辺を積分します。
I = \(\displaystyle\int\)\(\large{\frac{V_0\sinωt}{L}}\)dt
= \(\large{\frac{V_0}{L}}\)\(\displaystyle\int\)sinωt dt sinax の積分は -\(\large{\frac{1}{a}}\)cosax だから
= \(\large{\frac{V_0}{L}}\)\(\bigl(\)-\(\large{\frac{1}{ω}}\)cosωt\(\bigr)\) (ωt=0のときI最小、ωt=\(\large{\frac{π}{2}}\)のときI=0、ωt=πのときI最大)
= \(\large{\frac{V_0}{ωL}}\)\(\bigl(\)- cosωt\(\bigr)\)
これで電流 I の式が求められたわけですが、電圧の式 V = V0sinωt と見比べるために cos のところを sin の形に変形してみます。
上式に - cosωt = sin\(\bigl(\)ωt - \(\large{\frac{π}{2}}\)\(\bigr)\)
*
- cosα = sin\(\bigl(\)α - \(\large{\frac{π}{2}}\)\(\bigr)\) という式は三角関数の公式集に載ってないかもしれませんが、
cos\(\bigl(\)θ + \(\large{\frac{π}{2}}\)\(\bigr)\) = - sinθ という公式において θ + \(\large{\frac{π}{2}}\) = α と置き換えると求められます。(他にも様々な求め方があります。)
cos\(\bigl(\)θ + \(\large{\frac{π}{2}}\)\(\bigr)\) = - sinθ
⇒ cosα = - sin\(\bigl(\)α - \(\large{\frac{π}{2}}\)\(\bigr)\)
∴ - cosα = sin\(\bigl(\)α - \(\large{\frac{π}{2}}\)\(\bigr)\)
単位円を描いて考えてみますと、
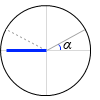 α が左図のような角度のときの - cosα というのは青線のことで、
α が左図のような角度のときの - cosα というのは青線のことで、
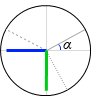 これを sin に置き換えるということは縦のラインに置き換えるということであり、つまり緑線の部分のことであります。
これを sin に置き換えるということは縦のラインに置き換えるということであり、つまり緑線の部分のことであります。
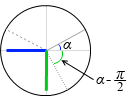 このときの角度は α - \(\large{\frac{π}{2}}\) です。
このときの角度は α - \(\large{\frac{π}{2}}\) です。
閉じる
を代入すると、
I = \(\large{\frac{V_0}{ωL}}\)\(\bigl(\)- cosωt\(\bigr)\)
= \(\large{\frac{V_0}{ωL}}\)sin\(\bigl(\)ωt - \(\large{\frac{π}{2}}\)\(\bigr)\) ……①
となり、電圧の式
V = V0sinωt
と見比べてみますと、電流の式の方は sin の中身に -\(\large{\frac{π}{2}}\) が付いていますので、位相が \(\large{\frac{π}{2}}\) 遅れていると分かります。\(\large{\frac{π}{2}}\) というのは 90° のことです。\(\large{\frac{1}{4}}\) 周期のことです。
別解
積分ではなく微分を使って上の電流の式を求める方法も説明しておきます。
電流を表す式を I = I0sin(ωt + φ) と仮定します(I0 は最大値)*y = Asin(Bt + C) という式があるとき、
 A は波の振幅(最大値)のことです。
A は波の振幅(最大値)のことです。
 B は波の角速度(揺れの細かさ)のことです。
B は波の角速度(揺れの細かさ)のことです。
 C は基準位置からの位相(タイミング)のズレのことです。
C は基準位置からの位相(タイミング)のズレのことです。
今回、電圧の式 V = V0sinωt に対して、
角速度は ω で変わらず、
最大値はどうなるかわからないので I0 とし、
位相のズレもどうなるか分からないので φ とし、
I = I0sin(ωt + φ) と仮定しました。
閉じる。
すると、コイルに発生する自己誘導起電力 VL は、
VL = - L\(\large{\frac{ΔI}{Δt}}\)
= - L\(\large{\frac{ΔI_0\sin(ωt+φ)}{Δt}}\) I0 は定数だから
= - LI0\(\large{\frac{Δ\sin(ωt+φ)}{Δt}}\) これを『誘導起電力の大きさ』と同じように微分します。sin(ωt+φ) の微分は ωcos(ωt+φ) です。
= - ωLI0cos(ωt+φ)
そして、上で説明したように、
V + VL = 0
であるわけですから、
V = - VL
であり、これに V = V0sinωt と VL = - ωLI0cos(ωt+φ) を代入すると、
V0sinωt = ωLI0cos(ωt+φ) ……②
となりますが、この等式がどうすれば成り立つか考えなければなりません。左辺も右辺も t によって様々な値をとりますが、三角関数の特徴を知っていれば、成り立つ条件が分かります。
sinx の最大値は 1 です。最小値は -1 です。x がどんな値であろうとも -1 ≦ sinx ≦ 1 です。つまり、V0sinωt の最大値は V0 です。
同様に、ωLI0cos(ωt+φ) の最大値は ωLI0 です。
次に、sinωt の部分と cos(ωt+φ) の部分が一致しなければなりませんが、sinα = cos(α - \(\large{\frac{π}{2}}\)) という公式 *
もし、sinα = cos(α - \(\large{\frac{π}{2}}\)) という式が三角関数の公式集に載ってなくても、
cos(θ + \(\large{\frac{π}{2}}\)) = - sinθ という公式において θ = α - π と置き換えると求められます。(他にも様々な求め方があります。)
cos(θ + \(\large{\frac{π}{2}}\)) = - sinθ
⇒ cos(α - π + \(\large{\frac{π}{2}}\)) = - sin(α - π)
∴ cos(α - \(\large{\frac{π}{2}}\)) = sin{-(α - π)}
∴ cos(α - \(\large{\frac{π}{2}}\)) = sin(π - α)
∴ cos(α - \(\large{\frac{π}{2}}\)) = sinα
単位円を描いて考えてみますと、
 α が左図のような角度のときの sinα は赤線のことで、
α が左図のような角度のときの sinα は赤線のことで、
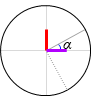 これを cos に置き換えるということは横のラインに置き換えるということであり、つまり紫線の部分のことであります。
これを cos に置き換えるということは横のラインに置き換えるということであり、つまり紫線の部分のことであります。
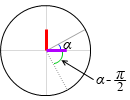 このときの角度は α - \(\large{\frac{π}{2}}\) です。
このときの角度は α - \(\large{\frac{π}{2}}\) です。
閉じる
があるので、φ = - \(\large{\frac{π}{2}}\) であれば、
sinωt = cos(ωt+φ) が成り立つといえます。
つまり、
V0 = ωLI0
φ = - \(\large{\frac{π}{2}}\)
であれば、②式が成り立ちます。
これらの条件を最初に仮定した I = I0sin(ωt + φ) の式に代入しますと、
I = \(\large{\frac{V_0}{ωL}}\)sin\(\bigl(\)ωt - \(\large{\frac{π}{2}}\)\(\bigr)\)
となり、①式と一致します。
ここまでのまとめ
コイルを流れる交流
電圧 V = V0sinωt
電流 I = \(\large{\frac{V_0}{ωL}}\)sin\(\bigl(\)ωt - \(\large{\frac{π}{2}}\)\(\bigr)\)
V0 = ωLI0
コイルを流れる交流は、電圧の位相より電流の位相の方が \(\large{\frac{π}{2}}\) 遅れます。
これは別の表現をすると、電圧の位相の方が電流の位相より \(\large{\frac{π}{2}}\) 進んでいる、ということになり、このことを式で表現すると、
V = V0sin\(\bigl(\)ωt + \(\large{\frac{π}{2}}\)\(\bigr)\)
I = \(\large{\frac{V_0}{ωL}}\)sinωt
となります。このように書き換えることも可能ということです。
3番目の式の V0 = ωLI0 は、電圧の最大値と電流の最大値の関係を表したものですが、実効値というものが最大値を単純に \(\large{\frac{1}{\sqrt{2}\ }}\) 倍したものであることから、Ve = ωLIe という関係も成り立っています。
(コンデンサーの場合と見比べてみてください。)
コイルのリアクタンス
V0 = ωLI0 という式は、よく見るとオームの法則の式 V = RI にそっくりです。
それぞれの式を \(\large{\frac{V_0}{I_0}}\) = ωL 、\(\large{\frac{V}{I}}\) = R と変形して眺めてみると、ωL や R は電圧と電流の比率を決めるもの、という見方ができます。
交流電源につないだコイルにおいては ωL のことをコイルのリアクタンス(誘導性リアクタンス)*reactance = react(反応する・反抗する)+ ance(量・程度を表す名詞語尾)
閉じるといい、量記号は XL *なぜ X を使うのか分かりません。
L は「コイル」のことで、レンツの法則のハインリヒ・レンツ Heinrich Lenz からです。
閉じるという文字を使います。単位は [Ω] オーム です。
コイルのリアクタンス
XL = ωL
 抵抗 R というものは、電荷の動きを原子が妨害するものです。ジュール熱が発生します。直流のときも交流のときも発生します。一方、コイルではジュール熱は発生しません*あくまでも理想的なコイルでの話ですが…。
抵抗 R というものは、電荷の動きを原子が妨害するものです。ジュール熱が発生します。直流のときも交流のときも発生します。一方、コイルではジュール熱は発生しません*あくまでも理想的なコイルでの話ですが…。
閉じる。
 コイルのリアクタンス XL というものは、電荷の動きを自己誘導起電力が妨害することを表すものです。
コイルのリアクタンス XL というものは、電荷の動きを自己誘導起電力が妨害することを表すものです。
”抵抗”も”リアクタンス”も電荷の動きを妨害するものであり、電圧と電流の比率を決めるものといえます。その単位 [Ω] は、今まで学習してきた意味を拡大して”リアクタンス”にも適用します。
このリアクタンスは交流のときのみ存在するものです。直流では、電流の流し始めと流し終わりの瞬間しか自己誘導が発生しません。それ以外では電荷の動きを妨害しません。たとえば、コイルと電球を接続した回路では、交流を流したときより直流を流したときの方が電球は明るく点灯します*直流電圧を掛けたときと、それと実効値が等しい交流電圧を掛けたときとを比較した場合の話です。
閉じる。
また、ω = 2πf であるので、振動数 f が大きいときの方がリアクタンス XL = ωL は大きくなり、
さらに、L = μn2lS であるので、巻きの密度が大きくて、長さが長くて、断面積の大きいコイルのときの方がリアクタンス XL = ωL は大きくなる、といえます。
電荷の動きをより妨害するということです。電流が小さくなるということです。
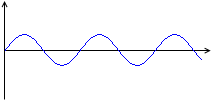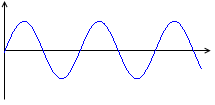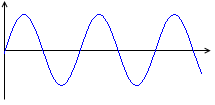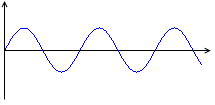
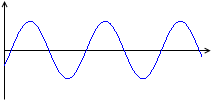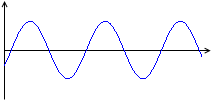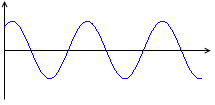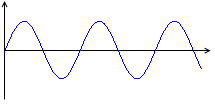
グラフ
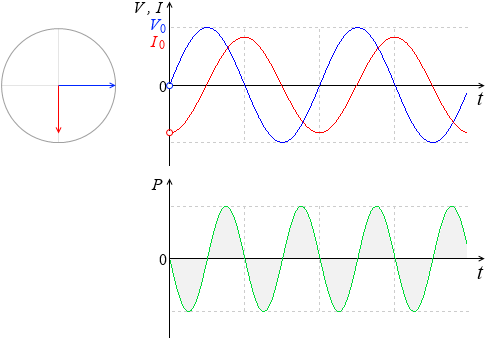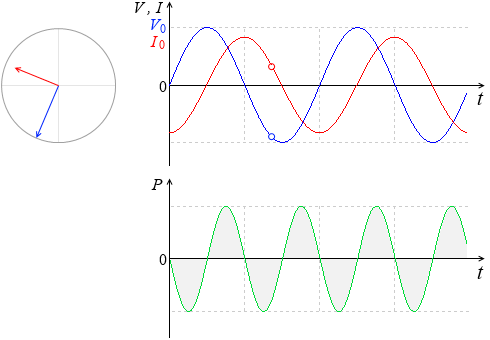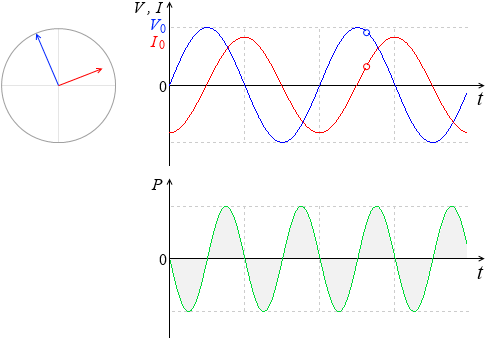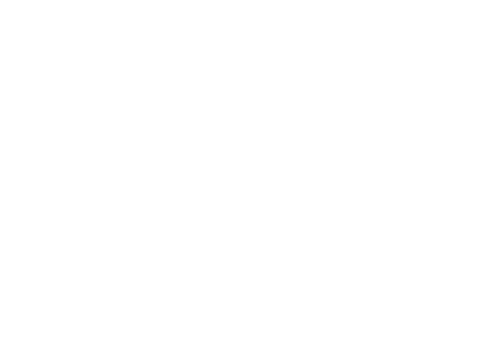 コイルを流れる交流電圧
コイルを流れる交流電圧
V = V0sinωt
と交流電流
I = \(\large{\frac{V_0}{ωL}}\)sin\(\bigl(\)ωt - \(\large{\frac{π}{2}}\)\(\bigr)\)
のグラフを描くと左図のようになります。
下に電力のグラフも描いてみました。
電流の方が位相が \(\large{\frac{π}{2}}\) 遅れています。(コンデンサーの場合と見比べてみてください。)
電力
電力というものは電流と電圧を掛けたものです。
電流の式は I = \(\large{\frac{V_0}{ωL}}\)sin\(\bigl(\)ωt - \(\large{\frac{π}{2}}\)\(\bigr)\) ですが、この式はもともと変形前は、
I = \(\large{\frac{V_0}{ωL}}\)\(\bigl(\)- cosωt\(\bigr)\)
でした。ここに V0 = ωLI0 を代入します。
I = I0\(\bigl(\)- cosωt\(\bigr)\) = - I0cosωt
この電流の式と、電圧の式 V = V0sinωt を掛け合わせて電力 P の式を導き出しますと、
P = I × V
= - I0cosωt × V0sinωt
= - I0V0 cosωt × sinωt 2倍角の公式 sin2θ = 2sinθcosθ を適用します
= - I0V0 \(\large{\frac{1}{2}}\)sin2ωt
= - \(\large{\frac{1}{2}}\)I0V0 sin2ωt
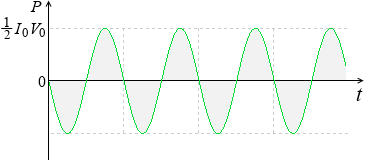 これをグラフにしたものが上で示した電力のグラフです。最大値が \(\large{\frac{1}{2}}\)I0V0 であり、角速度が ω から 2ω に増えています。
これをグラフにしたものが上で示した電力のグラフです。最大値が \(\large{\frac{1}{2}}\)I0V0 であり、角速度が ω から 2ω に増えています。
この曲線は 0 を中心にして振動しているので、和をとる(時間平均をとる)とトータルで 0 になります。電力の総和が 0 、これはつまり、交流を流したコイルでは電力が消費されない、ということです。ジュール熱が発生しないということです。このことは、ばねを揺らすようなことに例えられます。押してもその分、押し返されて、トータルで仕事をしない、というようなことです。*
電力はスカラーであるはずとお思いの方にとっては「トータルで 0 になる」というのはおかしな話であるかもしれませんが、これの意味は、たとえば電荷が基準位置より右に行ったら正、左にいったら負で、その和をとると 0 になるというような意味です。
『ばね振り子の力学的エネルギー』項においては、エネルギーは、右に行ったときも正、左に行ったときも正、と考えたわけですが、これは微視的なスパンで考えているからです。1往復の中で、中心からどのくらい離れたらエネルギーはどのくらいになるのかを考えたわけです。
もし巨視的なスパンで考えて、何万往復する中でエネルギーがどれくらい減衰していくかを考えるような場合には、右に10cm行ったら正、左に9.9cm行ったら負、また右に9.8cm行ったら正、左に9.7cm行ったら負、とカウントしていくのが妥当です。
閉じる
コンデンサーの場合のグラフと比べると、違いは上下が反転していることだけです。