ホール効果

ホール効果

ホール効果とは

電流が流れている物体に磁場を掛けると、電流をになう荷電粒子（キャリアといいます）がローレンツ力を受け、物体の端に移動し、そのことによって物体内に電位差（=起電力=電場）が生じます。この現象をホール効果＊19世紀のアメリカの物理学者エドウィン⋅ホール Edwin Hall が発見しました。「ホール効果」のホールは人の名前です。正孔（hole）が由来ではありません。別の単語の hall は会館、集会場という意味があります。

『電流が磁場から受ける力』項で、電流が流れる導線は磁場から力を受けることを説明し、『ローレンツ力』項で、その力はローレンツ力であると説明しましたが、そのとき実は、導線内で、電荷の偏りにより、電流と磁場に垂直な方向に電位差が生じていたのです。
　閉じるといいます。ローレンツ力を打ち消すかのようなはたらきをします。

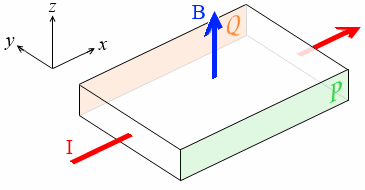左図のような直方体の物体を考えます。y軸の負の方向の面をP面、正の方向の面をQ面とします。x軸の正の向きに I [A] の電流が流れていて、z軸の正の方向に磁束密度 B [T] の磁場が掛かっているとします。

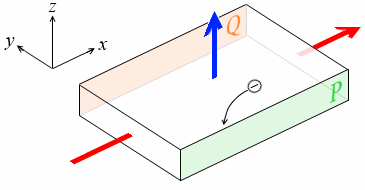この物体が導体で、電流をになうキャリアが自由電子の場合、この自由電子は x軸の負の方向に進もうとしますが、ローレンツ力を受け、P面の方向に曲げられます。

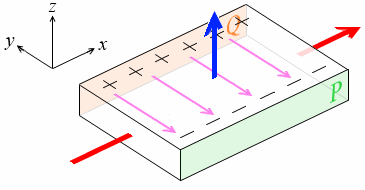このことによって、P面側に自由電子が多く分布し、Q面側にはあまり分布しなくなります。つまり、Q面は正に帯電しP面は負に帯電し、Q面からP面の方向に電位差（=起電力=電場）が生じます。これがホール効果です。ホール効果によって発生した電位差をホール電圧といいます。

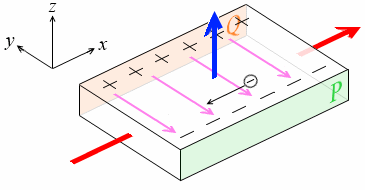さらに、自由電子はホール電圧による力も受けます。ローレンツ力の向きとホール電圧による力の向きは逆です。今の場合、ホール電圧の向きはQ面からP面への方向です。それによって負電荷である自由電子はQ面側へ吸い寄せられます。始めのうちは自由電子はローレンツ力によってP面側に集められますが、それが増えるとホール電圧による逆向きの力が強くなり、ローレンツ力とつり合います。つまり、自由電子のすべてがP面側に集まるわけでなく、ローレンツ力とホール電圧による力がつり合うような位置にいる自由電子については結局まっすぐ進むことになります。＊このことは、
P面側に負電荷が集められ過ぎると、押し合いへし合いをして少し戻される、
と考えることもできます。

これらの動作は実際には、時間とともに徐々に進むというわけではなく、電源を入れるなり、磁場を掛けるなりした瞬間に一瞬にして行われます。
　閉じる

ホール電圧の大きさ

自由電子がまっすぐ進むようになったとき、つまりローレンツ力とホール電圧による力がつり合ったときの、ホール電圧の大きさを求めてみます。

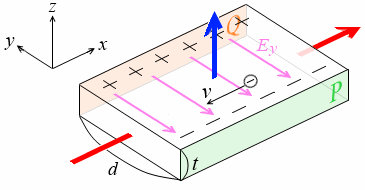物体の z軸方向の厚さを t [m] 、y軸方向の大きさを d [m] 、自由電子の電気量を -e [C] 、速さを v [m/s] 、物体中の自由電子（キャリア）の数密度を n [個/m3] 、新たにつくられる y軸方向の電場を Ey [V/m] ＊もともと物体には電流が流れているわけで、電流が流れているということはその方向に電場が発生しているわけで、電流の方向は x軸の方向ですから、もともとある電場を表すと Ex とでも表すことができます。この電場と新たにつくられる電場を明確に区別したいので、新たにつくられる方の電場を Ey という風に y を付けて表現しました。
y軸の負の方向を向いているので -Ey と表現してもいいかもしれません。
　閉じる、ホール電圧を VH [V] とします。

１つの自由電子に着目したとき、
この自由電子が、新たにつくられた y軸方向の電場 Ey から受ける力の大きさは、

　　　　eEy　　（ F = qE において q=e、E=Ey ）

この自由電子が受けるローレンツ力の大きさは、

　　　　evB　　（ f = qvBsinθ において q=e、sinθ=1）

であり、この２つの力がつり合っているのだから、

　　　　eEy = evB

　　∴　Ey = vB

となります。そして、電圧というものは電場の大きさに距離を掛けたものだから、求めるホール電圧は、

　　　　VH = Eyd = vBd　　……①

となります。

物体中のキャリアの数密度を調べられる

電流 I は、

　　　　I = envS

と表せますが、今、S = td ですので、

　　　　I = envtd

となります。これを変形して、

　　　　v = \(\large{\frac{I}{entd}}\)

とし、上の①式に代入すると、

　　　　VH = vBd = \(\large{\frac{I}{entd}}\)Bd = \(\large{\frac{IB}{ent}}\)

となります。

物体中のキャリアの数密度 n は、VH、I、B、t を測定して上式に代入することにより求めることができます。

数密度 n が分かっている物体であれば、VH、I、t を測定して上式に代入することにより磁束密度 B を求めることができます。このとき磁場測定に使う小片物体をホール素子といいます。

電流をになう荷電粒子（キャリア）が正孔の場合

『電流』項で、電流は自由電子の動きのことであると説明しました。しかし半導体という物質においてはそうではありません。電子が電流のにない手であることに変わりはないのですが、自由電子ではない電子が電流のにない手になっています。

ちょっとだけ説明しますと、
普通の導体を流れる電流というのは、『正電荷』項で示したアニメーションのように、

12個の座席 に12個の負電荷 があるような状態なのですが、
n型半導体と呼ばれるものは、12個の座席 に13個の負電荷 があるような状態で、
p型半導体と呼ばれるものは、12個の座席 に11個の負電荷 しかないような状態で、
p型半導体のときは開いた座席 が自由電子のように動きまわります。電荷は正です。この開いた座席のことを正孔（hole）といいます。正孔の電荷は正なので正孔が動く向きと電流の向きは一致します。

導体のときはキャリアが自由電子 -e で、
n型半導体のときはキャリアが電子 -e で、
p型半導体のときはキャリアが正孔 e です。

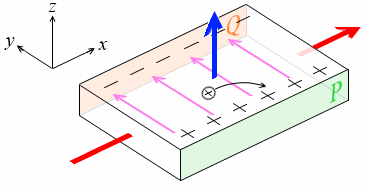測定する物体がp型半導体のとき、正孔はローレンツ力を受けP面側に集まります＊今、電流は x軸正の方向に流れていて、正孔もそれと同じ向きに動いていて、フレミングの左手の法則を適用すると、ローレンツ力はP面に向かう方向です。
導体、n型半導体における電子も、p型半導体における正孔も、同じ方向に力を受けるということです。電子は x軸負の方向へ進みながらP面方向へ曲げられます。正孔は x軸正の方向へ進みながらP面方向へ曲げられます。
電荷の正負が違うからローレンツ力の方向も違うのではないかと考えてしまうのは間違いです。電流の向きは同じです。順を追って考えていってフレミングの左手の法則を適用すれば、電子も正孔も同じ向きに力を受けることがお分かりいただけると思います。
　閉じる。正孔の電荷は正なので今度はP面が正に帯電しQ面が負に帯電します。つまり新たにつくられる電場が逆向きです。ホール電圧の正負が逆になるのです。しかし今度はキャリアの電荷が正なので、ホール電圧による力の向きはQ面への方向です。自由電子のときと変わりません。キャリアが負のときでも正のときでも、Q面への方向に力を受けるということです。

＊ ・・・・・というのがキャリアが正孔の場合における原理の説明です。
・・・が
なぜ正孔がP面に集まるのか、そのとき電子はどうしてるのか、本当の原理は私にはわかりません。
難しい理屈でそうなっているようです。すみません。。。
　閉じる

この原理によって、P面とQ面の電荷の正負を測定すれば（VHの正負を測定すれば）、物体がn型半導体なのかp型半導体なのかが判別できます。

↑ ↓