剛体にはたらく力のつり合い

剛体にはたらく力のつり合いの条件

『力のつり合い』の項で力のつり合いについて説明しましたが、これはあくまでも対象物が質点であること、もしくは質点とみなせることを前提としたものでした。質点の運動状態が変わらない場合、そこにはたらく力はつり合っている、ということでした。しかし質点と違って剛体には並進運動だけでなく回転運動もありますから、回転運動に関しても運動状態が変わらない、という条件を付け加えないと、本当に力がつり合っているとはいえません。つまり、力のモーメント（回転力）のつり合いについても考慮しなければならないのです。

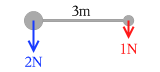たとえば左図のような剛体を考えてみます。

右側に 1.0N の重力が掛かる鉄球1、左側に 2.0N の重力が掛かる鉄球2があって、それらを結ぶ鉄棒は、十分硬いが重さが無く、長さが 3.0m であるとします。＊鉄棒部分の重さが無い、と仮定していますので、これはつまり現実にはあり得ない仮想モデルです。
　閉じる

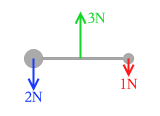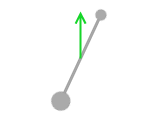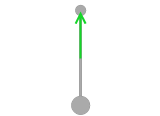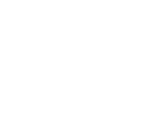この物体を空中にとどまらせるとき、何N の力で上に引っ張ればよいかというと、3.0N です。3.0N で上に引っ張れば並進運動はしなくなります。しかしこれだけではくるんと回転してしまうかもしれません。回転運動もしないようにしてはじめて『力がつり合った』ということになります。

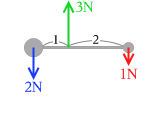小学校の理科の実験を思い出してください。くるんと回転しないようにするには左から 1:2 に内分する位置を支えればいいと分かると思います。天秤をつり合わせるには、（重さ）×（長さ）が等しくなればいいのです。小学校の実験で学んだことはまさに『力のモーメント＝（力）×（腕の長さ）』のことだったのです。

その支点を中心として3つの力のモーメントの和を考えてみます。

支点を左回りに回転させようとする向きを正とします。

すると、鉄球1による力のモーメントは　（力）×（腕の長さ）= -1.0[N] × 2.0[m] = -2.0[N・m]
鉄球2による力のモーメントは　+2.0[N] × 1.0[m] = +2.0[N・m]
上に引っ張る力の力のモーメントは　+3.0[N] × 0[m] = 0[N・m]

3つの力のモーメントを足しますと、
　　-2.0[N・m] + 2.0[N・m] + 0[N・m] = 0[N・m]
となります。和が 0 なので、回転しません。　……(a)

もし、左から 2:1 に内分する位置を支点とするとどうなるか考えてみます。

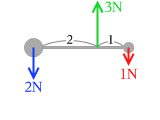鉄球1による力のモーメントは　-1.0[N] × 1.0[m] = -1.0[N・m]
鉄球2による力のモーメントは　+2.0[N] × 2.0[m] = +4.0[N・m]
上に引っ張る力の力のモーメントは　+3.0[N] × 0[m] = 0[N・m]

3つの力のモーメントを足しますと、
　　-1.0[N・m] + 4.0[N・m] + 0[N・m] = +3.0[N・m]
となります。0 ではありません。左回りに回転してしまいます。

ちなみに、左から 1:2 に内分する位置を支えた場合で、力のモーメントの中心を無理やり鉄球1の位置に設定して、それらの和を求めてみますと、

鉄球1による力のモーメントは　1.0[N] × 0[m] = 0[N・m]
鉄球2による力のモーメントは　+2.0[N] × 3.0[m] = +6.0[N・m]
上に引っ張る力の力のモーメントは　-3.0[N] × 2.0[m] = -6.0[N・m]

3つの力のモーメントを足しますと、
　　0[N・m] + 6.0[N・m] - 6.0[N・m] = 0[N・m]
となります。和が 0 なので、回転しません。上の(a)の場合と一致します。

つまり、力がつり合っている場合、力のモーメントの中心はどこに設定してもいいのです。問題を解くときは一番計算が楽になる位置を力のモーメントの中心と設定します。この話は回転の中心は任意の位置に設定できるという考えと通じるものがあります。

まとめます。

剛体にはたらく力を \(\vec{F}_1\)、\(\vec{F}_2\)、\(\vec{F}_3\)、… とし、任意の点のまわりの \(\vec{F}_1\) による力のモーメントを M₁、\(\vec{F}_2\) による力のモーメントを M₂、\(\vec{F}_3\) による力のモーメントを M₃、… とすると、剛体にはたらく力のつり合いの条件は以下のように表せます。

ベクトルかスカラーか

力はベクトルなので①の上部にはベクトルを表す→が付いてますが、力のモーメントはベクトルではなくスカラーなので②式の上部には→は付いていません。＊大学物理では力のモーメントもベクトルとして扱います。
　閉じる

どちらか一方を満たすとき

①式だけを満たすときというのは、剛体の並進運動の運動状態は変化せず、回転運動の運動状態が変化します。

②式だけを満たすときというのは、剛体の並進運動の運動状態が変化し、回転運動の運動状態は変化しません。

①式に関して

①式に関しては『力のつり合い』で説明した通りであり、

x成分、y成分に分けて表すと次のようになります。

F_1x + F_2x + F_3x + … = 0
F_1y + F_2y + F_3y + … = 0

また、力を平行移動させれば、閉じたn角形ができます。

②式に関して

②式は、任意の点のまわりの力のモーメントの和が 0 となってつり合っている、という意味なのですが、実は、①式が成り立っている場合、どこか特定の1点で②式が成り立つと、それ以外のどの点においても自動的に②式が成り立つという性質があります。

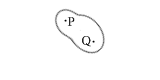P点で回転していなければ、Q点でも回転していません。

感覚的に当たり前のことですが、式を使って証明してみます。

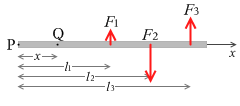2次元だと複雑になるので1次元の棒で考えます。

棒に3つの力がはたらいているとします。考えやすくするため、力の向きは棒に垂直であるとします。特定の点Pを左端にとり、棒が伸びる方向にx軸をとります。それぞれの力の作用点の位置を l₁、l₂、l₃ とし、点Pから x だけ離れた任意の点をQとします。

いま、①式が成り立っているという前提なので、
　　　　F₁ + F₂ + F₃ = 0　　（上図の場合では F₂ は右回りの向きなので、左式の F₂ の値は負です）

そして、P点に関して②式が成り立っているとすると、その力のモーメントの和は 0 であり、
　　　　M_P = F₁l₁ + F₂l₂ + F₃l₃ = 0

このときQ点に関する力のモーメントの和 M_Q を考えてみますと、
　　　　M_Q = F₁(l₁ - x) + F₂(l₂ - x) + F₃(l₃ - x)
　　　　　　= F₁l₁ + F₂l₂ + F₃l₃ - (F₁ + F₂ + F₃) x
　　　　　　= 0 - 0
　　　　　　= 0

となり、①式が成り立っているときは、M_P = 0 ならば M_Q = 0 といえます。

任意の点のまわりの力のモーメントの和

上式をさらによく見てみますと、M_P が 0 でなくても、
　　　　M_Q = F₁l₁ + F₂l₂ + F₃l₃ - (0) x = M_P
であり、つまり、①式が成り立っていれば、M_Q = M_P ということであり、

要するに、①式が成り立っていれば、任意の点のまわりの力のモーメントの和は変わらない、ということがいえます。

合力が 0 ならば、回転力の大きさは、どこを中心に設定にしても同じなのです。

3力の作用線は1点で交わる

平行でない3力について、それらが剛体にはたらいていてつり合っているとき、すなわち①式、②式が成り立っているとき、3力の作用線は1点で交わる、という性質があります。

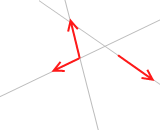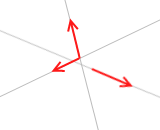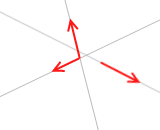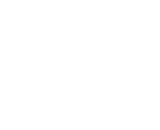
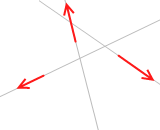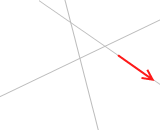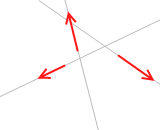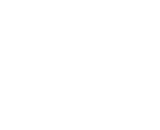まず3力の内の2力について力のモーメントの和を考えます。この2力は平行ではないので必ず交点があります。この交点をPとします。この2力を作用線上を動かすことによって交点Pの位置まで移動します。そしてこの交点Pにおける2力のモーメントの和を考えると、それは 0 です。なぜなら、どちらの力のモーメントとも交点Pからの距離が 0、すなわち（腕の長さ）が 0 であるからです。

残りの3番目の力の作用線について考えてみます。いま3力はつり合っているのだから、②式が成り立っています。つまり、3力の力のモーメントの和は 0 です。そして、3力の内の2力の力のモーメントの和は上で示したとおり 0 なのだから、残りの力のモーメントは 0 になります。つまり、（腕の長さ）が 0 です。なぜかというと、力のモーメント＝（力）×（腕の長さ） であり、いま3力が存在するといっているのだから（力）が 0 ということはないので、（腕の長さ）が自動的に 0 になるからです。（腕の長さ）とは交点Pからの距離です。それが 0 です。3番目の力は作用線上を動かせば交点Pの位置にくることができるということです。すなわち3番目の力の作用線は交点Pを通ります。

というわけで、剛体において平行でない3力がつり合っているとき、その作用線は1点で交わるといえます。また逆に、作用線が1点で交わらないときは、平行でない3力はつり合っておらず剛体は動いてしまう、といえます。平行な場合はそもそも作用線が交わることができないのでこの定理は使えません。

たとえ力が4つ以上ある場合でも、2つを1つに合成して全部で3力と見なせば上の定理が使えます。