パスカルの原理

単位面積当たりに掛かる力

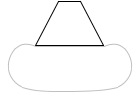台形の形をした固い物体をスポンジのような柔らかいものに押し付けるとき、広い面を押し付けたときと、

小さい面を押し付けたときでは、凹む度合いが違います＊降り積もった雪の上にハイヒールで立つと沈み込みます。かんじきを履けば沈み込みません。
　閉じる。このようなときは、押し付ける力の絶対量よりも、単位面積当たりどのくらいの力で押し付けているかの方が重要になります。＊たとえば、雨の量を評価するときに、全体で何リットル降ったかより、単位時間当たり、単位面積当たり、何リットル降ったか、という方が重要です。閉じる

このような、単位面積当たりに掛かる力のことを圧力といいます。量記号は P を用います＊pressure（圧力）から。もしかすると Pascal の P かも。
大文字の P だったり小文字の p だったりします。閉じる。力を F [N] 、面積を S [m²] ＊S の語源については諸説あります。sum、summation、square、space、surface、…閉じるとすると以下のように表せます。

単位は [Pa] パスカル です＊17世紀のフランスの物理学者 ブレーズ・パスカル Blaise Pascal より。閉じる。1m² 当たり 1N の力がはたらくときの圧力が 1Pa です。1[Pa] = 1[N/m²] です。大気圧を表すときに用いられる [atm] という単位もあります。

垂直成分のみ

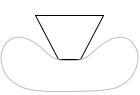
面に作用する力の大きさや、面が動いた距離、などというものを考えるときは、面に垂直な成分だけを考えます。

面に平行な成分を考えてしまうと、それは自動的に面の大きさを考慮していることになってしまいますし、面の摩擦係数を考慮しなければならなくなります。

というわけで、圧力の向きは面に垂直です。

等方的に伝わる力

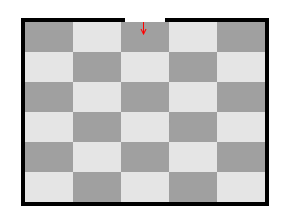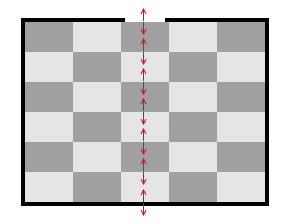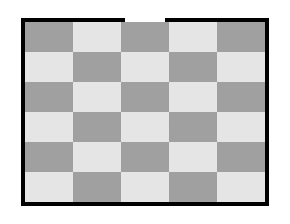左図のようにブロックを並べると、力は直線的に伝わります。（物体表面には摩擦が無いものとします。重力も無いものとします。以下同様。）

このように交互に並べると、力は広がりながら伝わります。

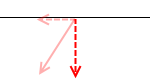
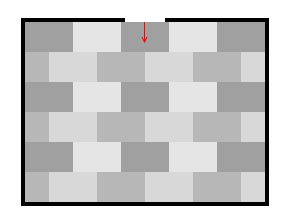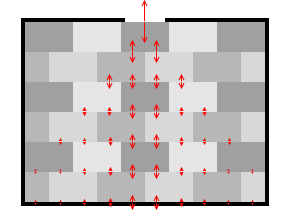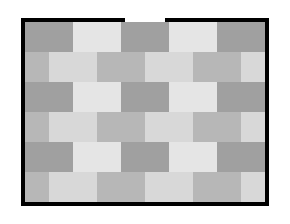
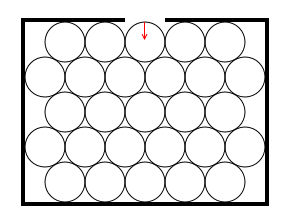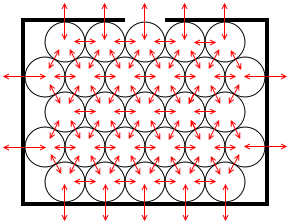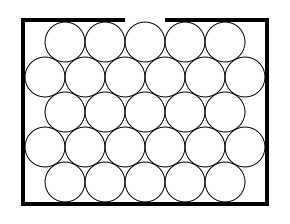球体を隙間なく並べると、力はあらゆる方向に等方的に伝わります。球体は潜り込んで突き上げることができます。（左図の赤矢印の長さは不正確ですが＊特に、端っこの球体の力の大きさは不正確です。中ほどの球体の等方的に広がる力の様子をご覧ください。

各微小部分は静止していますので、力がつり合っているということであり、微小部分内の各力のベクトルを平行移動させると閉じた多角形（左図では六角形）ができます。さらに、各微小部分、壁に掛かる力すべてを総計すると 0 になります。閉じる、雰囲気はだいたいこんな感じです。あくまでも無重力です。）

このとき、力の向きはあらゆる面に垂直です。球体はあらゆるものに垂直に接します。

パチンコ玉を水槽に満たすと規則正しく並び、力が等方的に伝わります。パチンコ玉の形状が球だからです。サイコロを水槽に満たしても力は等方的には伝わりません。形状が立方体だからです。

球という形こそがパスカルの原理の根本原因です。球が流体力学のスタート地点なのです。

パスカルの原理

物質には、固体、液体、気体、という3種類の状態、物質の三態というものがあり、このうち液体と気体は自由に形を変えることができ、これらを流体といいます。"流"体といってもここで考える流体は流れている流体（水流や風など）ではなく静止している流体です。高校物理における流体とは静止流体のことです。

流体が密閉容器の中に入れられていて、各分子が静止している場合、あらゆる地点の圧力は等しくなります。パスカルの原理といいます。流体の微小部分（分子）にはたらく力はあらゆる方向に等方的に伝わります。そしてそれが静止している場合、それは力がつり合っているということですから、これはつまり、あらゆる地点の圧力が等しいということです＊どこか一箇所だけ力が強い部分があればその部分は押し合いへし合いに勝ってズレ動くことになります。ズレ動いていって力がつり合ったところで止まります。結果的にどこもかしこも力がつり合うことになります。閉じる。どこか一箇所の圧力を高めると、全体の圧力が高まります。＊張力がどこもかしこも同じ大きさであることと同じ原理です。閉じる

このパスカルの原理は高校物理の教科書に載っていないのですが、とてもとても重要な原理ですので絶対覚えてください。＊パスカルの原理を理解していないと、物理現象の多くのことが理解できません。水圧、浮力はもちろん、粉塵爆発、突沸、過冷却などもパスカルの原理の理解が必要です。また、社会科学においてもパスカルの原理を意識していないと本質を見抜くことができません。パスカルの原理を意識すれば、世界恐慌が再び起こってしまう可能性があることを理解できます。閉じる

　　流体 + 密閉 + 静止 ＝ パスカルの原理 ＝ あらゆる地点の圧力が等しい

例

密閉容器の中の流体の圧力が 56Pa であれば、どこもかしこもあらゆる地点が 56Pa です。

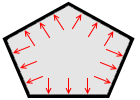壁に掛かる圧力も 56Pa です。

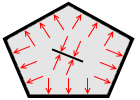投入した板に掛かる圧力も 56Pa です。

圧力の向きは常に垂直です。

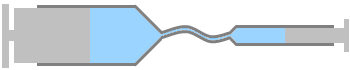大きい注射器と小さい注射器による押し合い合戦では、小さい方が勝ちます。

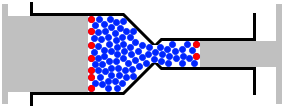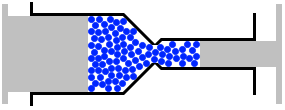左図の例では大きい方のピストンに7個の球体、小さい方のピストンに2個の球体が接触してますが、1つの球体に 1N の力が掛かっているとすると、大きいピストンには 7N 、小さいピストンには 2N の力が掛かっていることになるので、小さいピストンが勝ちます。小さいピストンを押す人は 2N より大きい力で押せばいいですが、大きいピストンを押す人は 7N より大きい力で押さなければなりません。（あくまでザックリした話です。球体の数がもっと多くないと正確な話はできません。）

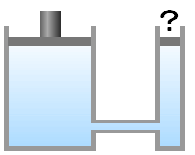シリンダーの断面積が\(\large{\frac{1}{10}}\)なら重りも\(\large{\frac{1}{10}}\)で済みます。\(\large{\frac{2}{10}}\)の重りを載せれば、小さい方のシリンダーが勝ちます。

油圧ポンプの原理です。断面積が10倍なら、10倍の重りを持ち上げられます。10倍の力を生み出せるのです。