力学的エネルギーが保存されない運動
非保存力がはたらく場合
『単振り子の力学的エネルギー』『ばね振り子の力学的エネルギー』は力学的エネルギーが保存される場合の話でしたが、本項では力学的エネルギーが保存されない場合の話をします。
保存力のみがはたらく運動においては力学的エネルギーは保存されますが、非保存力もはたらく運動においては力学的エネルギーは保存されません。保存力というのは重力や弾性力や静電気力などのことで、非保存力というのは摩擦力や空気抵抗や人の手の力などのことです。
持ち上げられる球
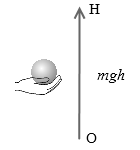 初めOの位置にあった質量 m の球を h だけ手で持ち上げて静止させると球の力学的エネルギーは mgh になります。
初めOの位置にあった質量 m の球を h だけ手で持ち上げて静止させると球の力学的エネルギーは mgh になります。
球のO点での力学的エネルギーは 0 (運動エネルギー 0 、位置エネルギー 0 )。
球のH点での力学的エネルギーは mgh (運動エネルギー 0 、位置エネルギー mgh )。
力学的エネルギーは、保存されず、mgh だけ増えています。これは手が球に mgh の仕事をしたためです。
式で表現すると以下のようになります。
ΔE = EH - EO = ( KH + UH ) - ( KO + UO ) = ( 0 + mgh ) - ( 0 + 0 ) = mgh = 手がした仕事 W
あらい水平面を進む物体
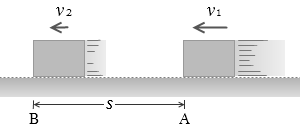 摩擦のあるあらい水平面を質量 m の物体が進んでいるとします。手の力は加えないとします。物体は摩擦力によって減速します。空気抵抗を考えないとすると、物体は摩擦力のみによって減速します。摩擦力の大きさを F とすると摩擦力のした仕事は - Fs です。力の向きが運動の向きと逆なので仕事は負でありますし、物体が仕事を受け取ったかどうかでいうと、物体の運動エネルギーが減少しているので、負の仕事を受け取ったといえます。
摩擦のあるあらい水平面を質量 m の物体が進んでいるとします。手の力は加えないとします。物体は摩擦力によって減速します。空気抵抗を考えないとすると、物体は摩擦力のみによって減速します。摩擦力の大きさを F とすると摩擦力のした仕事は - Fs です。力の向きが運動の向きと逆なので仕事は負でありますし、物体が仕事を受け取ったかどうかでいうと、物体の運動エネルギーが減少しているので、負の仕事を受け取ったといえます。
式で表現すると以下のようになります。
ΔE = EB - EA = ( KB + UB ) - ( KA + UA ) = ( \(\large{\frac{1}{2}}\)mv22 + 0 ) - ( \(\large{\frac{1}{2}}\)mv12 + 0 ) = \(\large{\frac{1}{2}}\)mv22 - \(\large{\frac{1}{2}}\)mv12 = - Fs(摩擦力がした仕事 W)
(ちなみに、動摩擦係数を μ' とすると動摩擦力の大きさは F = μ'mg であるので、- Fs = - μ'mgs です。)
ΔE = W
このようにみてきますと、
非保存力がはたらくと力学的エネルギーは保存されなくなってしまうが、その差分は非保存力がした仕事になっている
とわかると思います。
式で書くと、ΔE = W です。エネルギーの原理に似ています。エネルギーと仕事は等価です。
エネルギー保存の法則
力学的エネルギーが保存されていなくても、非保存力がした仕事までをも考えに入れると、その全てのエネルギーは保存されています。このことをエネルギー保存の法則といいます。球を持ち上げる運動では、人の手に内在していたエネルギーが球に移ったのです。あらい面をすべる物体の運動では、物体が持っていたエネルギーが、摩擦熱で床面を温めることに使われたのです。電気エネルギーが位置エネルギーに変わったり、運動エネルギーが熱エネルギーに変わったり、エネルギーの形態は変化しますが、エネルギーの総量は一定で変わらないのです。
法則の整理
ここまで似たような法則が3つ出てきたので整理しておきます。
| エネルギーの原理: | 下のエネルギー保存の法則のうち、非保存力がはたらく場合で、運動エネルギーに着目した原理。 |
|---|
| 力学的エネルギー保存の法則: | 下のエネルギー保存の法則のうち、保存力のみがはたらく場合で、力学的エネルギーに着目した法則。 |
|---|
| エネルギー保存の法則: | 物体の持つ力学的エネルギー、電気的なエネルギー、熱力学的なエネルギー、保存力のする仕事、非保存力のする仕事、等を全て考えに入れると、その総量は物体の状態が変化しても一定であるという法則。 |
|---|