qHBF9

（問3）
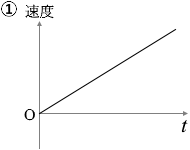
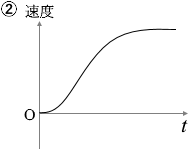
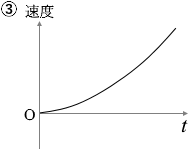
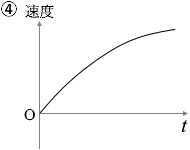
小物体には重力が掛かり、その力によって加速していくわけですが、その力は一定であり、摩擦も無いので、すなわち運動方程式より、加速度も一定です。加速度が一定ということは、等加速度直線運動あるいは自由落下運動のように、速度は一定の割合で大きくなっていきます。

答えは ① です。

③と間違えやすいですが、③は速度でなく変位を表すグラフです。

（問4）
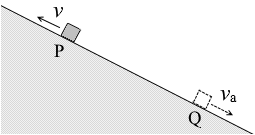
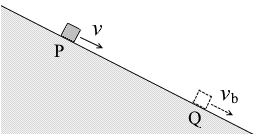
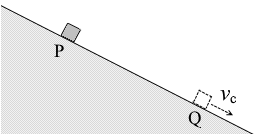
小物体の質量を m 、斜面の仰角を θ 、小物体の斜面方向の加速度を a 、重力加速度の大きさを g 、点Pと点Qの距離を l 、高低差を h とします。

（解法1）
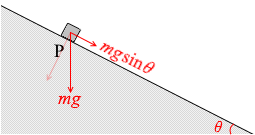小物体に掛かる重力は mg で、運動方向の成分は mgsinθ であり、運動方程式を立てますと、

　　　　ma = mgsinθ

　∴　　a = gsinθ

となりますが、g の値は一定であるので gsinθ も一定であるわけです。そうしますとこの運動は鉛直投射運動において、g を gsinθ としたもの、と考えることができます。（たとえば sinθ=0.6 なら g を 0.6g に変更しただけのもの。あるいは単なる等加速度直線運動、と考えてもいいです。）

それぞれの場合について、鉛直投射（あるいは等加速度直線運動）の時間 t を含まない式を立てますと（右下方向を正とする）、

(a)
　　　　v_a² - (-v)² = 2(gsinθ)l

　∴　　v_a² = v² + 2glsinθ

　∴　　v_a = \(\sqrt{v^2+2gl\sinθ}\)

(b)
　　　　v_b² - v² = 2(gsinθ)l

　∴　　v_b² = v² + 2glsinθ

　∴　　v_b = \(\sqrt{v^2+2gl\sinθ}\)

(c)
　　　　v_c² - 0² = 2(gsinθ)l

　∴　　v_c² = 2glsinθ

　∴　　v_c = \(\sqrt{2gl\sinθ}\)

答えは ⑥ v_a = v_b > v_c です。

（解法2）
もう一つの解法はエネルギーに着目するやり方です。

それぞれの場合について、力学的エネルギー保存の法則の式を立てますと、

(a)
　　　　\(\large{\frac{1}{2}}\)mv² + mgh = \(\large{\frac{1}{2}}\)mv_a²

　∴　　v_a² = v² + 2gh

　∴　　v_a = \(\sqrt{v^2+2gh}\)

(b)
　　　　\(\large{\frac{1}{2}}\)mv² + mgh = \(\large{\frac{1}{2}}\)mv_b²

　∴　　v_b² = v² + 2gh

　∴　　v_b = \(\sqrt{v^2+2gh}\)

(c)
　　　　0 + mgh = \(\large{\frac{1}{2}}\)mv_c²

　∴　　v_c² = 2gh

　∴　　v_c = \(\sqrt{2gh}\)

よって、 ⑥ v_a = v_b > v_c です。

h = lsinθ ですので、2種類の解法で得られた双方の値は同じものです。

また、慣れてくれば解法2の各式の左辺だけを思い浮かべ、

　　\(\large{\frac{1}{2}}\)mv² + mgh

　　\(\large{\frac{1}{2}}\)mv² + mgh

　　0 + mgh

これらを比較して、答えは v_a = v_b > v_c だな、と暗算できるようになります。

（『qI2Q9』もご参照ください）