実効値

交流の電圧の大きさは表現に困る

直流の電圧は時間が変わっても一定ですので、その電圧の大きさは 30V 、などと表現できますが、

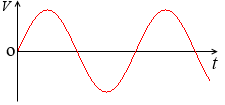交流の電圧は時間によって変わるので一概に 30V とはいえません。t=2s のときは 27V で、t=4s のときは -23V だったりします。（このような瞬間々々の値を瞬時値といいます。）

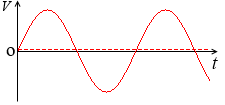かといって、各瞬時値の平均をとると 0V になってしまいます。

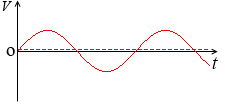しかも、最大値＊波の振幅のことです。『誘導起電力の大きさ』で説明した V₀ のことです。
　閉じるが大きいときも小さいときも 0V となってしまいます。

ですので、各瞬時値の平均値というものは交流の大きさを表現するのにはふさわしくありません。

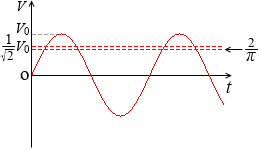
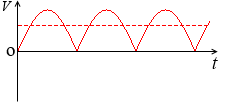別の考え方として、負の瞬時値を正に置き換えてその平均をとって（絶対値の平均をとる）、交流の大きさを表現することもあります。交流の平均値といいます。積分して求めるのですが、その大きさは最大値の \(\large{\frac{2}{π}}\) (≒0.64) 倍になります＊なぜ \(\large{\frac{2}{π}}\) 倍になるか補足ページで解説しましたのでお読みください。
　閉じる。ですがこの値は高校物理では使われません。

たとえば、「電圧の大きさは 30sinωt [V] 」と表現してしまえば正確でいいじゃないか、ということなんですが、これはこれで、だったら ω の値はいくらなんだ、ということになってしまいますし、この表現だと瞬時値を意識してしまいます。そんなこんなで、交流の大きさを表現するのによく用いられるのが実効値という値です。

交流の実効値

実効値というのは、抵抗器に交流を流したときに消費される電力が平均値をとる瞬間の電圧や電流の値のことです。別の見方をすると、抵抗器に交流を流すときにその効力は直流に換算するとどのくらいになるかを示す量、ともいえます。

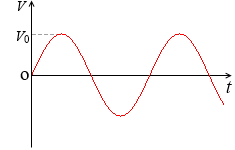　　V = V₀ sinωt （V₀ は V の最大値）

で表される交流電圧 V [V] を R [Ω] の抵抗に加えると、オームの法則より、

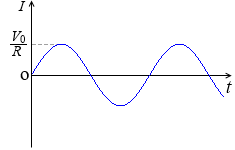\(\large{\frac{V}{R}}\) = \(\large{\frac{V_0}{R}}\)sinωt と表される電流が流れます。\(\large{\frac{V}{R}}\) = I [A] 、\(\large{\frac{V_0}{R}}\) = I₀ [A] とおきますと、

　　I = I₀ sinωt

です。グラフは左図のようになります。周期や周波数は変わらず、振幅が変わります。

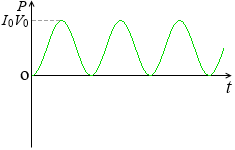この抵抗で消費される電力 P [W] は、

　　P = I V = (I₀ sinωt)×(V₀ sinωt)
　　　= I₀V₀ sin²ωt

となります＊なぜこのようなグラフになるか補足ページで解説しましたのでお読みください。
　閉じる。周期が半分になり、負の値をとらなくなります。-1 ≦ sinωt ≦ 1 でありますが2乗したものは 0 ≦ sin²ωt ≦ 1 であり、すなわち 0 ≦ I₀V₀sin²ωt ≦ I₀V₀ です。

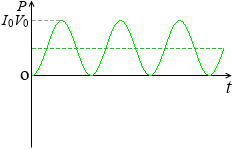この電力の平均値は、

　　P = \(\large{\frac{1}{2}}\)I₀V₀

です。グラフの曲線は I₀V₀ の半分の位置を中心に振動しています。

この値をとる瞬間の電圧を V_e 、電流を I_e ＊e は effective value（実効性のある値）の頭文字。
　閉じる とおきます。つまり、I_eV_e = \(\large{\frac{1}{2}}\)I₀V₀ とします。

オームの法則より、V = RI 、V₀ = RI₀ 、V_e = RI_e ですので、

　　　　I_eV_e = \(\large{\frac{1}{2}}\)I₀V₀

　∴　\(\large{\frac{V_\rm{e}}{R}}\)V_e = \(\large{\frac{1}{2}}\)\(\large{\frac{V_0}{R}}\)V₀

　∴　　 V_e² = \(\large{\frac{1}{2}}\)V₀²

　∴　　　V_e = \(\large{\frac{1}{\sqrt{2}\ }}\)V₀

これが交流電圧の実効値であり、同様に、

　　　　I_eV_e = \(\large{\frac{1}{2}}\)I₀V₀

　∴　I_e RI_e = \(\large{\frac{1}{2}}\)I₀ RI₀

　∴　　 I_e² = \(\large{\frac{1}{2}}\)I₀²

　∴　　　I_e = \(\large{\frac{1}{\sqrt{2}\ }}\)I₀

これが交流電流の実効値です。＊\(\large{\frac{1}{\sqrt{2}\ }}\) という値は 約0.707 であり、上で示した平均値の係数 \(\large{\frac{2}{π}}\) ≒ 0.64 よりわずかに大きくなっています。


　閉じる

V = V₀ sinωt と表していた交流電圧は 実効値 V_e を使って V = \(\sqrt{2}\)V_esinωt とも表せます。同様に、
I = I₀sinωt と表していた交流電圧は 実効値 I_e を使って I = \(\sqrt{2}\)I_esinωt とも表せます。

直流との比較

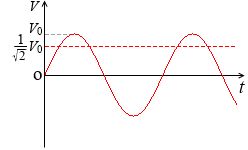V = V₀ sinωt で表される交流電圧を代表する値は、実効値 V_e = \(\large{\frac{1}{\sqrt{2}\ }}\)V₀ で、

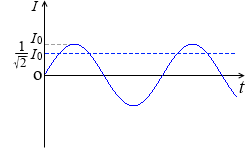このとき R [Ω] の抵抗に流れる電流は I = \(\large{\frac{V_0}{R}}\)sinωt = I₀sinωt であるわけですが、この交流電流を代表する値は、実効値 I_e = \(\large{\frac{1}{\sqrt{2}\ }}\)I₀ であるわけです。

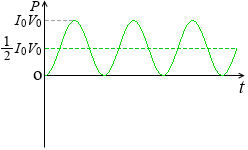そしてこのとき抵抗で消費される電力は P = I₀V₀ sin²ωt であるわけですが、その平均値は P = \(\large{\frac{1}{2}}\)I₀V₀ です。

この値は"直流"電圧 V_dc = \(\large{\frac{1}{\sqrt{2}\ }}\)V₀ を R [Ω] の抵抗に掛けたときに消費される電力と同じです。このとき流れる"直流"電流は I_dc = \(\large{\frac{1}{\sqrt{2}\ }}\)I₀ です＊dc は 直流 direct current から。
　閉じる。

家庭用電源

家庭用電源の電圧は 100V ですが、実はこれは実効値の値です。最大値はその \(\sqrt{2}\) 倍の 141.4V です。-141.4V ~ 141.4V を行ったり来たりしています。その周波数は東日本では 50Hz（西日本では 60Hz）です。これは角周波数に直すと ω = 2πf ≒ 2×3.14×50 (60) = 314 (377) rad/s になります。ですから、家庭用電源を実効値でなく式で表現するとすれば、（ V = V₀ sinωt に当てはめて ）
　　V = 141.4sin(314t)
ということになります。これの実効値が 100V というわけです。