実効値の補足
交流の平均値の求め方
本編で紹介した交流の平均値（絶対値平均）の求め方を説明します。
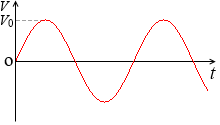V = V0 sinωt [V] で表される交流電圧の負の部分を正に置き換えますと、
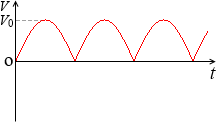このようになります。
このグラフの各瞬時値の平均を求めるということは、この曲線と t 軸で囲まれる部分の面積を求めて、
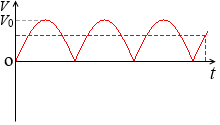平らにならして、横方向の長さで割って、縦の高さを求めるということです。
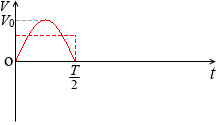半周期分の面積 S を積分を使って求めてみます。
S = \(\displaystyle\int_{0}^{\frac{T}{2}}\)V0 sinωt dt
= V0\(\displaystyle\int_{0}^{\frac{T}{2}}\)sinωt dt sinax の積分は -\(\large{\frac{1}{a}}\)cosax
= V0\(\Bigl[-\frac{1}{ω}\cosωt\Bigr]^{\frac{T}{2}}_0\)
= - \(\large{\frac{V_0}{ω}}\)\(\Bigl[\cosωt\Bigr]^{\frac{T}{2}}_0\)
= - \(\large{\frac{V_0}{ω}}\)\(\Bigl(\)cosω\(\large{\frac{\small{T}}{2}}\) - cos0\(\Bigr)\) ωT = 2π を代入
= - \(\large{\frac{V_0}{ω}}\)\(\Bigl(\)cos\(\large{\frac{2π}{2}}\) - cos0\(\Bigr)\)
= - \(\large{\frac{V_0}{ω}}\)\(\Bigl(\)cosπ - cos0\(\Bigr)\)
= - \(\large{\frac{V_0}{ω}}\)(- 1 - 1)
= - \(\large{\frac{V_0}{ω}}\)(- 2)
= 2\(\large{\frac{V_0}{ω}}\) ω = \(\large{\frac{2π}{T}}\)を代入
= 2\(\large{\frac{V_0T}{2π}}\)
= \(\large{\frac{V_0T}{\Large{π}}}\)
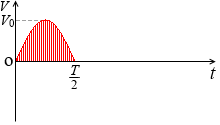この面積 S = \(\large{\frac{V_0T}{π}}\) を横の長さ \(\large{\frac{T}{2}}\) で割りますと、
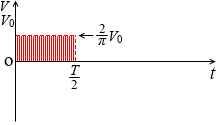高さが \(\large{\frac{V_0T}{π}}\)÷\(\large{\frac{T}{2}}\) = \(\large{\frac{V_02}{π}}\) = \(\large{\frac{2}{π}}\)V0 と割り出せます。
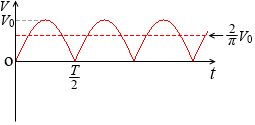というわけで、V = V0 sinωt の平均値（絶対値平均）は最大値 V0 の \(\large{\frac{2}{π}}\)倍です。
P = I0V0 sin2ωt のグラフ
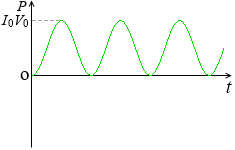P = I0V0 sin2ωt のグラフの波の形がなぜこのようになるか、説明します。
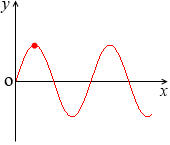具体的な例を挙げてみますと、たとえば、
y = 3sinx の x = 1.5 のときの値は y ≒ 3.0 で＊
1.5rad という量は 1.570796rad よりやや小さい量ですが、
1.570796rad というのは 3.141592rad の半分で、
つまり \(\large{\frac{π}{2}}\)rad （度数法でいうところの 90°）に近い量です。
すなわち sin1.5 というのは sin\(\large{\frac{π}{2}}\)=1.0 に近い値で、
3sin1.5 は 3.0 に近い値です。
閉じる、
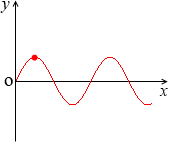y = 2sinx の x = 1.5 のときの値は y ≒ 2.0 で、
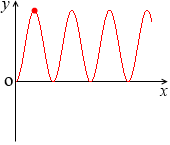y = (3sinx)×(2sinx) = 6sin2x の x = 1.5 のときの値は y ≒ 6.0 で、これは上の２つの値を掛けた 3.0×2.0 の値です。
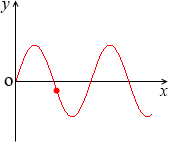さらにたとえば、
y = 3sinx の x = 3.4 のときの値は y ≒ -0.77 で、
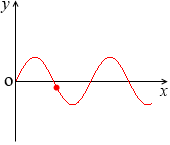y = 2sinx の x = 3.4 のときの値は y ≒ -0.51 で、
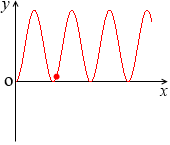y = (3sinx)×(2sinx) = 6sin2x の x = 3.4 のときの値は y ≒ 0.39 で、これは (-0.77)×(-0.51) の値です。
別の観点から考えるとすれば、P = I0V0 sin2ωt の式を変形してしまった方が分かりやすいかもしれません。三角関数の2倍角の公式 cos2α = 1 - 2sin2α を使います＊
2倍角の公式は加法定理から導くことができます。
sin(α + β) = sinαcosβ + cosαsinβ
sin(α - β) = sinαcosβ - cosαsinβ
cos(α + β) = cosαcosβ - sinαsinβ
cos(α - β) = cosαcosβ + sinαsinβ
加法定理の４つの式のうち３番目の式において α = β とおきます。
cos(α + α) = cosαcosα - sinαsinα
cos(2α) = cos2α - sin2α
= (1 - sin2α) - sin2α
= 1 - 2sin2α
変形しますと、
sin2α = \(\large{\frac{1}{2}}\) - \(\large{\frac{1}{2}}\)cos2α
です。
閉じる。すると、
P = I0V0 sin2ωt
= I0V0 (\(\large{\frac{1}{2}}\) - \(\large{\frac{1}{2}}\)cos2ωt)
となりますが、この式のグラフがどのようになるか考えてみます。(\(\large{\frac{1}{2}}\) - \(\large{\frac{1}{2}}\)cos2x) のグラフについて探ります。
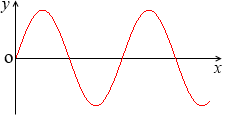まず、y = sinx のグラフはこうです。
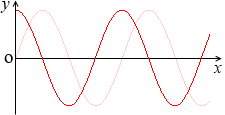次に、cosx = sin(x + \(\large{\frac{π}{2}}\)) の関係から、
y = cosx のグラフは y = sinx を \(\large{\frac{π}{2}}\) だけ左にずらしたものといえます。
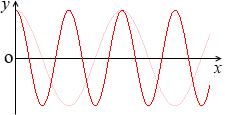そして、周期を半分にしたものが、
y = cos2x
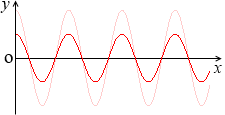そして、振幅を半分にしたものが、
y = \(\large{\frac{1}{2}}\)cos2x
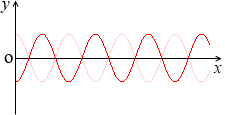そして、上下反転させたものが、
y = - \(\large{\frac{1}{2}}\)cos2x
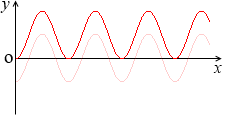そして、上に \(\large{\frac{1}{2}}\) だけずらしたものが、
y = \(\large{\frac{1}{2}}\) - \(\large{\frac{1}{2}}\)cos2x
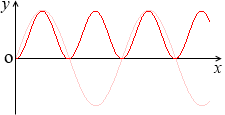つまり、これが y = \(\large{\frac{1}{2}}\) - \(\large{\frac{1}{2}}\)cos2x = sin2x のグラフであり、すなわち、
P = I0V0 sin2ωt の波の形はこのようになる、ということです。
実効値の係数は波の形を示唆している
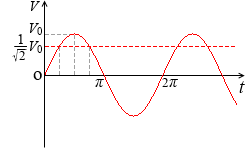V = V0 sinωt で表される交流電圧の実効値は Ve = \(\large{\frac{1}{\sqrt{2}\ }}\)V0 であるわけですが、これは位相でいうと \(\large{\frac{π}{4}}\) 、\(\large{\frac{3}{4}}\)π 、… のときの値です。
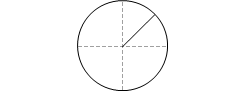単位円で描くと左図のような位置です。\(\large{\frac{1}{\sqrt{2}\ }}\) というのは sin\(\large{\frac{π}{4}}\) という意味でもあります。
sin\(\large{\frac{π}{4}}\) の位置で、電圧と電流を掛けた電力の値が平均の値になるというのは、sin関数独特の現象です。\(\large{\frac{1}{\sqrt{2}\ }}\) という係数は、交流電圧の変化の仕方がsinカーブを描くということを示唆しています。
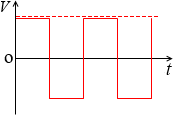電圧の変化の仕方がsinカーブを描かない場合、たとえば矩形波（くけいは）を描く場合は、実効値は最大値と同じになります。Ve = V0 です。別の書き方をすれば Ve = \(\large{\frac{1}{\sqrt{1}\ }}\)V0 です。＊
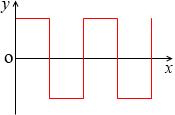このような曲線（電圧）と
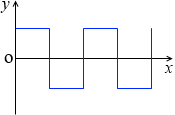このような曲線（電流）を掛け合わせると
このような曲線（電力）になります。平均値＝最大値 です。
閉じる
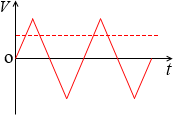あるいは、電圧の変化の仕方が三角波を描く場合は、実効値は最大値の \(\large{\frac{1}{\sqrt{3}\ }}\)倍、つまり Ve = \(\large{\frac{1}{\sqrt{3}\ }}\)V0 となります。＊
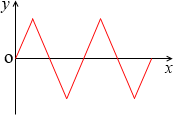このような曲線（電圧）と
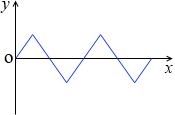このような曲線（電流）を掛け合わせると
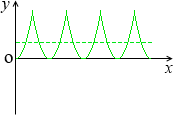このような曲線（電力）になります。そして、平均値＝ \(\large{\frac{1}{3}}\)×最大値 です。（ ヒント：x2 を積分すると \(\large{\frac{1}{3}}\)x3 です。）
閉じる
このように実効値の係数は波の形を示唆しています。統計学的にいえば分散の度合いを示しています。
さらに、この係数は絶対値平均の係数より常に大きくなっています。たとえば、\(\large{\frac{1}{\sqrt{2}\ }}\) というのは 約0.707 であり、本編あるいは当ページ上方で示した絶対値平均の係数 \(\large{\frac{2}{π}}\) ≒ 0.637 より大きくなっています。