平面上の変位と速度と加速度

直線上と平面上

前項において変位と速度と加速度について説明しましたが、それは直線上の運動（1次元）を念頭においたものでした。本項では平面上の運動（2次元）において、それらがどのように表現されるのかを説明します。

平面上を動くということは動く量の他に動く方向を意識しなければならず、ベクトルの導入が必要不可欠になります。直線上の運動も本当はベクトルで記述しなければいけないのですが、「右向きを + 、左向きを - 」などと定義することにより、まるでスカラーを扱っているかのように計算することが可能でした。しかし平面上の運動ではそうはいきません＊とはいっても高校物理の範囲においては、平面上の運動であってもベクトルを成分に分けて考えることによってスカラーであるかのように計算していくことが可能です。本格的にベクトルで計算をするのは大学に行って内積、外積について学んでからです。
　閉じる。

位置

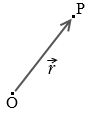直線上の運動においては位置を定めるときに、基準点から +3 の位置とか、-2 の位置とか、ベクトルでなくても表現できましたが、平面上の運動においては、基準点から北東方向へ 3m の位置とか、水平面から 30° 見上げた方向へ 2m の位置、などと必ずベクトルで表現しなければなりません。記号で表すときは、たいてい \(\vec{r}\) で表します。

変位

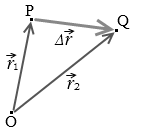変位についても、平面上の運動においてはベクトルで表さなければなりません。物体が点P（\(\vec{r_1}\)）から点Q（\(\vec{r_2}\)）に移動したときの変位 \(\Delta\vec{r}\) は、

　　\(\Delta\vec{r}\) = \(\vec{r_2}\) - \(\vec{r_1}\)

と表せます。( \(\vec{r_1}\) - \(\vec{r_2}\) とやると間違いなので気を付けてください。（後の状態）-（最初の状態）が正解です。）

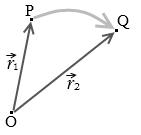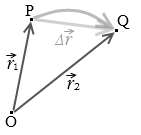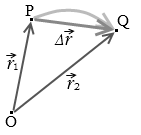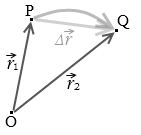そして、この変位は起点と終点しか問題にならず、途中経路のことは無視します。直線的に進んでも蛇行して進んでも変位は一緒です。\(\Delta\vec{r}\) = \(\vec{r_2}\) - \(\vec{r_1}\) です。

速度

速度ももちろんベクトルで表さなければなりません。

平均の速度

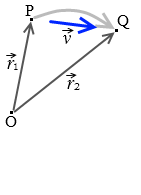速度は変位を時間で割ったものですから、速度を \(\vec{v}\)、点Pから点Qまでかかった時間を Δt とすると＊\(\vec{v}\) と \(\Delta\vec{r}\) はベクトルですが、Δt はスカラーです。閉じる、

　　\(\vec{v}\) = \(\large{\frac{\Delta\vec{r}}{\Delta t}}\)

と表せます。これは点Pから点Qに移動したときの平均の速度です。蛇行したとしても、途中で加速減速したとしても変わりません。\(\vec{v}\) = \(\large{\frac{\Delta\vec{r}}{\Delta t}}\) です。始点の位置と終点の位置と時間しか問題になりません。平均の速度の方向は変位ベクトルの方向と一緒です。

瞬間の速度

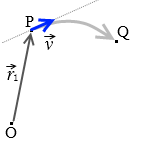そしてこのとき、Δt を限りなく小さくしていったとき（つまり \(\Delta\vec{r}\) も限りなく小さくしていったとき）の \(\vec{v}\) は点Pにおける瞬間の速度を表します。このときの \(\vec{v}\) の方向は曲線PQ上の点Pにおける接線の方向になっています。

加速度

加速度もベクトルで表します。

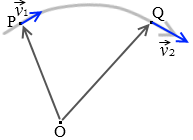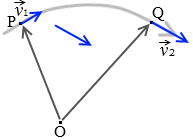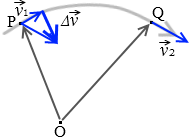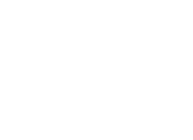点Pでの速度を \(\vec{v_1}\)、点Qでの速度を \(\vec{v_2}\) とすると、速度の変化分 \(\Delta\vec{v}\) は \(\Delta\vec{v}\) = \(\vec{v_2}\) - \(\vec{v_1}\) です。『平面上の相対速度』も参照してください。

平均の加速度

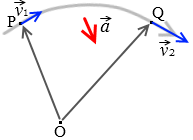加速度（\(\vec{a}\) とする）は速度の変化分を時間で割ったものですから、

　　\(\vec{a}\) = \(\large{\frac{\Delta\vec{v}}{\Delta t}}\)

と表せます。これは点Pから点Qに移動したときの平均の加速度です。蛇行したとしても、途中で加速減速したとしても変わりません。\(\vec{a}\) = \(\large{\frac{\Delta\vec{v}}{\Delta t}}\) です。始点の速度と終点の速度と時間しか問題になりません。

瞬間の加速度

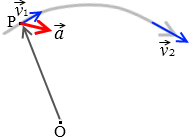そしてこのとき Δt を限りなく小さくしていったとき（つまり \(\Delta\vec{v}\) も限りなく小さくしていったとき）の \(\vec{a}\) は点Pにおける瞬間の加速度を表します。このときの \(\vec{a}\) の方向は接線の方向とは限りません。