相対速度 基礎物理範囲
相対速度
一般的に速度といったら、地表に立った観測者から見た物体の運動の速度のことをいいます。あるいは静止している基準点から見た物体の運動の速度のことをいいます。
いま、運動している物体が２つあって、どちらかに観測者が乗っていて、もう片方の物体を見ているとすると、静止している基準点から見たときの速度とは違ってきます。このときの物体Aから見た物体Bの速度を、Aに対するBの相対速度といいます。
A 
B
右向きを正とし、物体Aの速度を 1m/s、物体Bの速度を 2m/s とします。
静止している基準点から見たBの速度は 2m/s ですが、Aに乗っている観測者から見たBは 1m/s に見えます。Bが1秒間に2m進んでも、その間にAが1m進むので、Aから見たBは1mしか進んでいません。
つまりAに対するBの相対速度は、vAB = vB - vA = 2m/s - 1m/s = 1m/s 。＊
vAB の添字の付け方なんですが、
高校物理では「 vAB 」、大学物理では「 vBA 」とすることが多いです。ご注意ください。
閉じる
逆にBに乗っている観測者から見たAは -1m/s に見えます。Aが1秒間に1m進んでもその間にBが2m進むので、Bから見たAは負の方向へ1m進んでいるように見えます。
つまりBに対するAの相対速度は、vBA = vA - vB = 1m/s - 2m/s = -1m/s 。
A 
B
今度は、右向きを正とし、物体Aの速度を -1m/s、物体Bの速度を 2m/s とします。
Aに対するBの相対速度は、vAB = vB - vA = 2m/s - (-1m/s) = 3m/s 。
Bに対するAの相対速度は、vBA = vA - vB = -1m/s - 2m/s = -3m/s 。
＊たとえば、
●西向きに時速100kmで走っている電車の中で、東向きに時速100kmでボールを投げたらどうなるでしょうか？
→ 電車の外から見ている人にとっては、ボールは静止しています。
→ 電車の中で見ている人にとっては、ボールは時速100kmで動いています。
●その電車の中で、ラジコンのヘリコプターを浮遊させたらどうなるでしょうか？
→ 電車が動き始める前から飛ばせば、（電車の外から見ている人にとっては）ヘリコプターは静止している、（電車の中で見ている人にとっては）ヘリコプターは時速100kmで後方へと追いやられていく。
→ 電車が動き出した後から飛ばせば、（電車の外から見ている人にとっては）ヘリコプターは時速100kmで電車と共に動いている、（電車の中で見ている人にとっては）ヘリコプターは静止している。
●ろくろの上に、もう一つ、ろくろをひっくり返して載せるとどうなるでしょうか？
→ ひっくり返して上に載せたろくろの土台部分は、回転せずに静止します。
●光速の51%の速さのロケット同士がすれ違うときに、一方から相手を見たときの速さは光速を超えるでしょうか？
→ 光速は超えません。しかしここでは説明できません。大学に行って学んでください。
『慣性力』項の『様々な話題の整理』もご参照ください。
閉じる
～に対する
「Aに対するBの相対速度」という表現は、どっちが基準なのかわからなくなることがあります。慣れないうちは「～に対する」という言葉を「～を基準とした」に言い換えるようにしてみてください。「Aに対するBの相対速度」といったら「Aを基準としたBの相対速度」です。
また、相対速度を求める際に引き算をするときは （対象物）-（基準） です。これも間違いやすいので気をつけてください。
あるスタート地点から物体Bが北向きに1秒間に2m進み、物体Aが東向きに1秒間に2m進むとき、物体Aから見た物体Bの運動はどのようになるでしょうか。
このようになります。
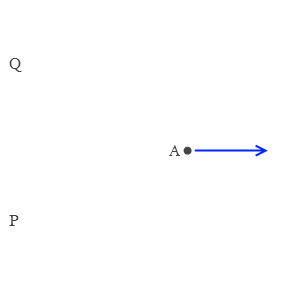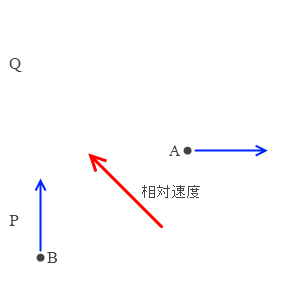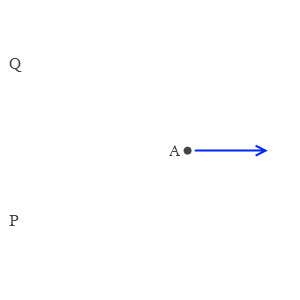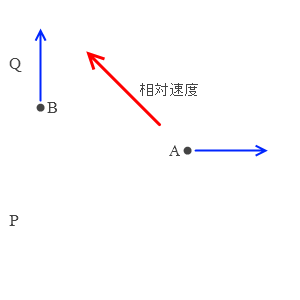そして相対運動を考える際、対象物Bは左図のPのような位置にあってもQのような位置にあっても、Aから見た相対速度は一緒です。（相対
Aが東に進むとき、Aからまわりを見るとすべての景色は西に動いています。ですのでBがどの地点で運動していようと、Aから見ると、（Bの動き）+（西向きの動き）となります。
\(\vec{A}\) - \(\vec{B}\) = \(\vec{A}\) + (-\(\vec{B}\))