水圧

水圧の原理

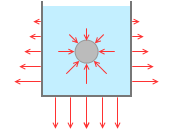容器の中に入れられた水は、容器側面や底面を押しています＊左図の容器は密閉されてませんが、だからといって上面には何も力が掛かってないわけではなく、水は上向きに大気を押しています。水面では、大気が下向きに水を押し、水が大気を上向きに押しています。左図ではそれらを省略しています。
　閉じる。水中に物体があればそれを押しています。また、水分子同士も押し合っています。このときの水の圧力を水圧といいます。（高校物理では静止している流体の圧力、静圧（静水圧）のみを取り扱います。川の流れやホースによる流水のような動圧（動水圧）については考えません。）

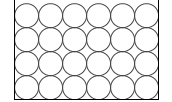左図のように水分子が並んでいるとします。隙間無く並んでいて静止しています。（実際には水分子はもっと複雑な配列で並んでいますし、各分子は揺れ動いています。左図は説明のための仮想モデルです。＊もし疑問がある場合は当サイトのご感想掲示板にて質問してください。この説明方法は筆者が独自に考えたものであり他の教材には載っていませんので。
　閉じる）

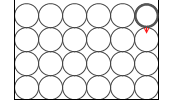右上の分子に着目してみますと、この分子には重力が掛かり、その下の分子を下に押しています。

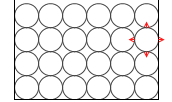押された分子は上に押し返す（作用⋅反作用の法則）と同時に左右下方向も押します。パスカルの原理により力は全方位に伝播するからです。（作用⋅反作用の法則とパスカルの原理を理解してないと水圧の原理は理解できません）

このとき、力の向きはあらゆる面に垂直です。

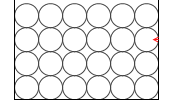押された壁は作用⋅反作用によって押し返しています。

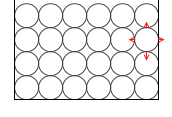そして、全方位に等しく伝播するはずのところが、分子自身の重さによって下方向の力が少し強くなります。

この下方向の力が少し強くなるというのが水圧の根本原理です。

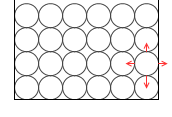少し強くなった力で押された3番目の分子はそれと同じ力で全方向に押そうとしますが、ここでもまた3番目の分子自身の重さによって下方向の力が少し強くなります。

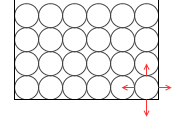4番目も同様です。

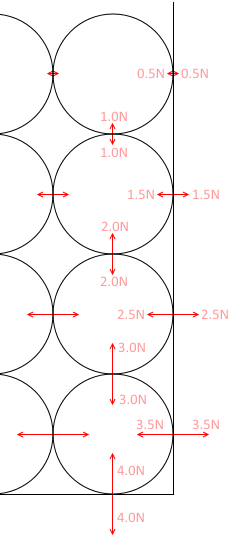拡大して説明します。

重さ 1.0 N (約102g) の球体が格子状に並んでいるとした場合、力の様子はこのようになります。＊ 横方向の 0.5N 等の力について疑問に思うかもしれませんが、それは

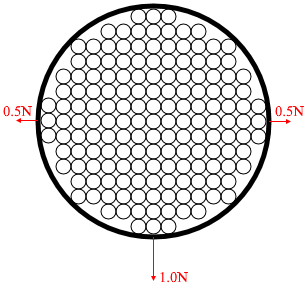
球体の中に更に無数の球体があって同じ原理による力がはたらいていると考えてください。
これは拡大して説明する場合はそうするしか仕方のないことですが、
大雑把に、1段目はすべての方向に 1N、2段目はすべての方向に 2N、3段目はすべての方向に 3N、と考えてしまってもいいです。
　閉じる

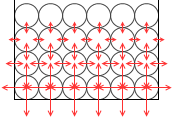これらの力をすべて図示すると左図のようになります。

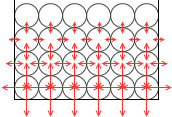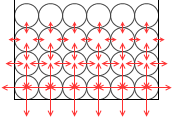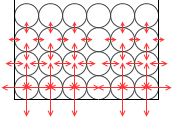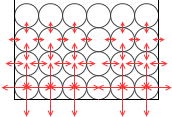横列の力を見比べるとその大きさは等しくなってますが、縦列の力を見比べると下に行くほどその大きさは大きくなってます。上から何段目であるかだけが水圧の大きさに関わってきます。水圧の特徴は、高さ（というか、深さ）のみによる、ということです。水圧の大きさは深さのみによるのです。

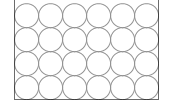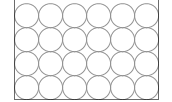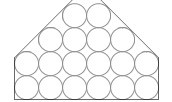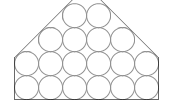たとえ容器の形が左図のように変化しても2段目や3段目の水圧は以前と変わりません。1段目が軽くなったので2段目、3段目にはたらく水圧も小さくなるように感じてしまうかもしれませんが、そうではありません。

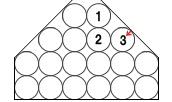左図の①の重さが②に掛かり、その力は全方位に伝播するので、③に影響を及ぼし、③は全方位に力を及ぼすので壁を斜め上に押します。そして壁は作用⋅反作用によって③を押し返します。このように壁からの押し返しがあるので、実は③には変形前と同じ圧力が掛かっているのです。

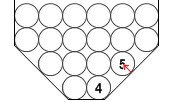たとえ容器が左図のように変わっても、同じことがいえます。

④は負担が増えて水圧が増しそうですが、そうではありません。⑤を容器の壁が支えているので、④の負担は増えません。容器の形が変わっても水圧は以前と変わらないのです。上から何段目であるかだけが水圧の大きさを決めるのです。

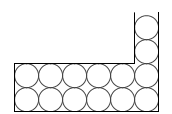このような容器の底面（容器の内側の底面）の圧力と、

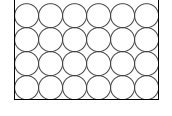このような容器の底面の圧力は同じです。

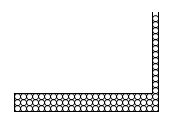このような容器の底面の圧力と、

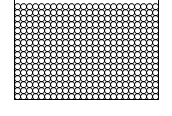このような容器の底面の圧力も同じです。

上図の容器には85粒入っていて、左図の容器には384粒入っているから、底面の圧力が異なる、と考えるのは間違いです。

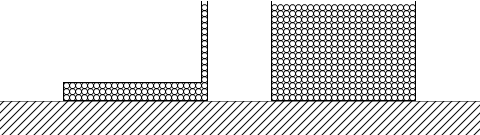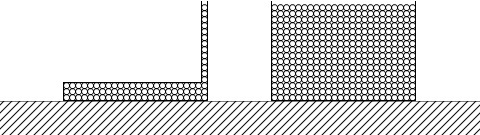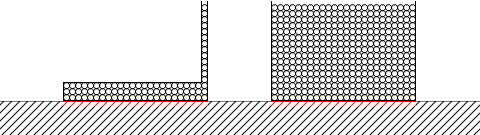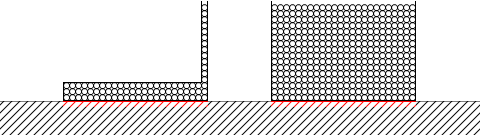もし、これらの容器が置かれた部屋の床に掛かる圧力というものを考えるのなら違いが出ますが、容器の底面の圧力に関しては違いが出ません。これはとても間違いやすいポイントです。

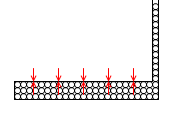下から3段目の粒たちは容器の上面とものすごい力で押し合いへし合いをしています。

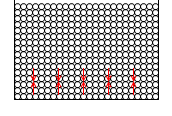内部的には、384粒あるときと同じ状態なのです。

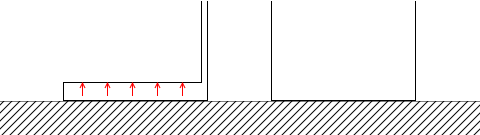外部的には、L字容器は上に押し上げられて、床面への負担が少なくなっています。だから外形的には軽いのです。＊たとえば、タイヤの空気圧を上げても、内部的には高圧になりますが、外部的には重さは変わりません。高圧になると、地面を強く押しそうですが、同時にタイヤの上面も押し上げられているので、外形的には重さは変わりません。

檻に閉じ込められた人間が、背伸びして天井と床面を強く押しても、外形的には檻の重さは変わりません。

外形的に重さが変わらなければ内部的にも圧力が変わらないはず、とか、
外形的に軽くなっていれば内部的にも圧力が弱まっているはず、と考えるのは間違いです。
　閉じる

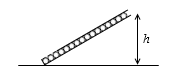さらにいいますと、左図のように斜めになっていた容器を、

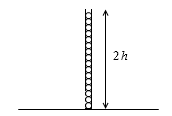立ててその高さが2倍になったとすると、底面の圧力も2倍になります。

このことは、知らない人、誤解している人がとても多いです。例えば、直径が1cmしかない細い管でも何十メートルもの高さにして水を満たせば、とてつもなく大きな圧力を得られます。

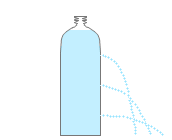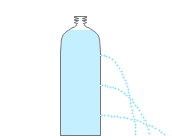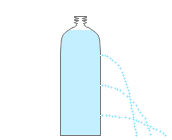ペットボトルに穴を開けたときの、水の出る勢いはこんな感じになります。

これらの特徴は水以外でも、油や空気でも成り立ちます。あらゆる流体で成り立ちます。パスカルの原理に重力の影響を加味したものがこれらの特徴です。（ただし、水圧の場合は容器に蓋がなくても重力があるのでいいのですが、パスカルの原理のみを考えるときというのは、容器が密閉されてなければなりません。分子が自由に容器外へ出られるような場合はパスカルの原理は成り立ちません。）

密度

単位体積当たりの質量のことを密度といいます＊電磁気分野では『磁束密度』という言葉があります。社会科学では『人口密度』という言葉があります。『密度』という言葉には混み具合という意味があります。
物理において単に『密度』といったら、単位体積当たりの質量のことです。
　閉じる。「密度が大きい」といったら、大きさの割に重いという意味で、「密度が小さい」といったら、大きさの割に軽いという意味です＊空気 1.1kg と、鉄 1.0kg では、空気の方が重いですw
　閉じる。密度の単位は [kg/m³] です。あるいは [g/cm³]、[kg/L] です。1 kg/m³ = 0.001 g/cm³ です。量記号は ρ （ろー）を用います＊ギリシア文字の小文字の ρ です。語源は分かりません。
ρ という量記号は抵抗率としても用いられます。
　閉じる。

水の密度は 1 kg/L = 1 g/cm³ = 1000 kg/m³ = 1 t/m³ です。
鉄が 7.87 g/cm³=7870 kg/m³ で、水銀が 13.5 g/cm³=13500 kg/m³ です。

比重という言葉もあります。固体、液体の物質については水の密度との比のことです。事実上、密度と同じ意味です。比重が 1.0 よりも大きい物質は水に沈み、1.0 よりも小さい物質は水に浮きます＊ドレッシングのボトルの中を見ると、油が浮いています。油の密度が水より小さいということです。
『浮き沈み』参照。
　閉じる。

牛乳の密度は水とほぼ同じで、約1.03kg/L です。スーパーで売っている1リットルの牛乳は 約1.03kg です。

水圧の式

水圧の大きさは深さのみによる、ということを上で説明しましたが、実際に他の物理量を使ってどのように表されるか考えてみます。

水分子１個の大きさと質量がわかればいいのですが、それらがわからなくても、水の密度から導き出すことができます。

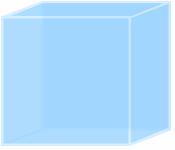1辺が 1m の水の立方体を考えます。水の密度は 1000kg/m³ なので、この立方体の質量は 1000kg です。重力加速度を 9.8m/s² とすると、重さは 9800N です。この力が 1m² の底面に掛かるので、底面の圧力は 9800Pa です（ [Pa] = [N/m²] ）。つまり、深さ 1m での水圧は 9800Pa です。

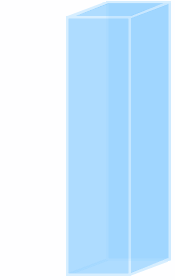さらに、高さ 2m、横 0.5m、奥行き 1m の直方体を考えると、この直方体の重さは 9800N で、底面積が 0.5m² なので、底面の圧力は 19600Pa であり、深さ 2m での水圧は 19600Pa ということになります。

同様にして、高さ 3m、横 0.333m、奥行き 1m の直方体を考えれば、深さ 3m での水圧は 29400Pa となります。

つまり、深さ h [m]、重力加速度 g=9.8[m/s²] の場合の水圧 p [Pa] は、以下のようになります。

もし、密度 1000kg/m³ の水に限らず、密度 ρ [kg/m³] の流体にも公式を適用するとすれば、

となります。さらに、実際にはコップの水もプールの水も海の水も上面は大気にさらされていて、空気の圧力、大気圧を受けます。大気圧を p₀ [Pa] とすれば、以下のようになります。