得もしないし損もしない
どのような経路をたどっても仕事は一緒
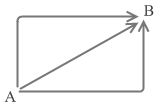物体を引き上げる際に、坂道を使っても、垂直に持ち上げても、仕事は一緒であると本編で説明しましたが、このことをもうちょっと広くいうと、A地点からB地点まで物体を運ぶとき、どの経路をたどっても仕事は一緒ということがいえます。経路のうち、水平部分では仕事は 0 です。（摩擦が無いことが前提です。）
動滑車を使うと必要距離が2倍
動滑車を使うと必要距離が2倍になるということがわかりにくい方は、動滑車が非常に小さくなって、ただの折り目になったものとしてイメージしてみてください。
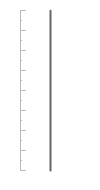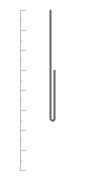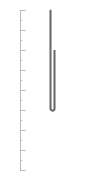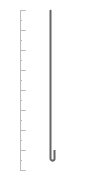さらに手のスタート地点を動滑車の位置とし、手のゴール地点を天井の位置とイメージすると理解しやすくなると思います。
こう考えると、動滑車の問題は幾何学の折り曲げの問題であるとわかります。糸の端の動きは折り曲げ点の動きの倍です。
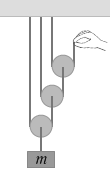このことが理解できれば、左図のような複雑な問題が出題されても、すぐに答えられるのではないでしょうか。
物体を h[m] 持ち上げるには手を 何[m] 持ち上げる？そのとき必要な力は 何[N]？そのときの仕事は 何[J]？
答えは、8h [m] 、\(\large{\frac{mg}{8}}\)[N] 、mgh[J] です。
仕事の原理は力のモーメントに似ている
仕事の原理は力のモーメントに似ています。力のモーメントにおいて、同じモーメントなら、回転軸から離れるほど力は少なくて済みます。回転軸から離れれば、実際に回転させようとするとき必要距離が大きくなります。力が小さくなっても距離が多く必要となります。仕事の原理と似ています。
同様に、車や自転車のギヤの原理にも似ています。小さい力で進むにはたくさん漕がなければなりません。