仕事の原理

仕事の原理

物体を引き上げる仕事について、坂道を引き上げる場合と鉛直上向きに引き上げる場合とで比較をしてみます。

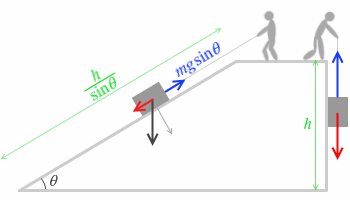物体の質量をどちらの場合も m [kg]、台の高さを h [m]、斜面の傾きを θ [rad]、重力加速度を g [m/s²]とし、斜面はなめらかであるとします。

（１）と（２）の結果が同じです。
（１）の場合、引き上げるのに必要な力は（２）に比べ、sinθ 倍に小さくなりましたが、同じ高さまで引き上げるための距離が \(\large{\frac{1}{\sin\theta}}\) 倍長くなったのです。θ=30°とすると、sin30°=\(\large{\frac{1}{2}}\) 。つまり、mg は半分の \(\large{\frac{1}{2}}\)mg 、h は倍の 2h になったのです。

一般に、道具や装置を使って小さな力で物体を動かそうとしても、その分、移動距離が長くなり、仕事で得をすることはありません。このことを仕事の原理といいます。

なお、このとき摩擦や道具の重さの影響は無視します。（仕事について考えるとき普通は重さの影響を受けないようゆっくり動かします。）

滑車における仕事の原理

下図のような動滑車における仕事の原理について考えてみます。

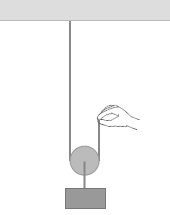滑車には動滑車というものと定滑車というものがあり、左図のように自由に動ける滑車を動滑車といい、『滑車で曲げられても』や『糸でつながれた物体』で示したような固定された滑車を定滑車といいます。定滑車は力の方向を変えるだけの役割しかありませんが、動滑車は少し複雑です。

また、張力の特徴として、つながった1本の糸にはたらく張力はどこもかしこも一定であることがいえます。

これらのことを踏まえて、動滑車に吊るされた質量 m の物体を h だけ引き上げるための仕事を求めてみます。

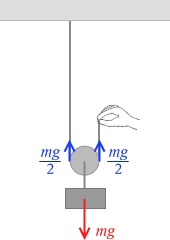まず引き上げるのに必要な力を求めます。その力は物体を静止させておくために必要な力と同じです。静止させておくために必要な力と同じ力でゆっくり引き上げるのです。

その力は \(\large{\frac{mg}{2}}\) です。mg のものを2本の糸で支えているので \(\large{\frac{mg}{2}}\) です。

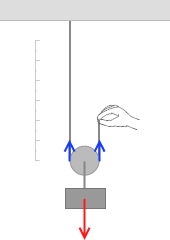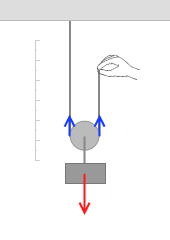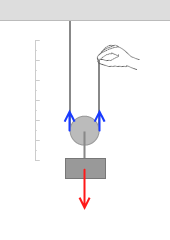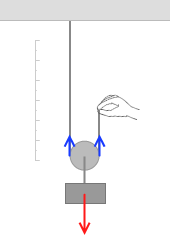次に引き上げる移動距離を考えてみます。左のアニメーションを見てもらうとわかると思いますが、動滑車を h だけ引き上げるには、手を 2h 動かさなければなりません。これが動滑車のキモです。動滑車を 1m 動かすには手を 2m 動かさなければならないのです。このことがわかりにくい方は補足ページをご覧ください。（なお、仕事を考える場合は、動かし方は普通ゆっくりです。左図のように素早く動かしたりしません。）

よって、求める仕事は、

　　W = 力×距離 = \(\large{\frac{mg}{2}}\) × 2h = mgh

です。

これは、動滑車を用いず、単純に手で物体を引き上げる場合の仕事 mgh と一緒です。つまり仕事の原理です。道具を使っても仕事は得をしないのです。別のいい方をすると、動滑車とは、必要な力を半分にし、必要な距離を2倍にする道具です。