運動エネルギー_補足

単位の演算

参考までに、ピストルの弾が粘土にした仕事から弾の運動エネルギーを求めた式において、単位の演算をやってみます。

　　　　W = Fs = - mas = \(\large{\frac{1}{2}}\)mv²

　　　　[J] = [N]・[m] = [kg]・[m/s²]・[m] = [kg]・[m/s]²

正負がややこしい

仕事について考えるとき正負の区別が難しくて混乱しやすいので、あらためて説明しておきます。

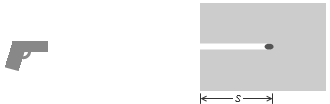ピストルの弾を粘土の塊に撃ち込む話では、右向きを正としたので、弾が粘土を押す力 F は右向きなので正。逆に、弾が粘土から受ける力は左向きなので負（ -F ）。弾の加速度は、右向きに進んでいるものがだんだんスピードを落とすのだから負。つまり a は負です。-a とは表現しませんでしたが負です。a は -3[m/s²] とか -5[m/s²] などという値をとるということです。F は負の値はとりません。F = 3[N] とか 5[N] などという値をとります。-F が負の値をとるのです。-F = -3[N] とか -5[N] などという値をとります。

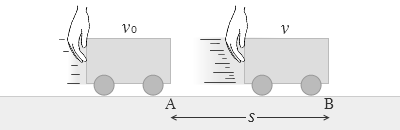台車を手で加速させる話では、右向きを正としたので、手の力は右向きなので正。右向きに進んでいるものがよりスピードを増すのだから加速度も正。

また、ピストルの弾の運動エネルギーを求める話は、エネルギーの原理の式

　　　　\(\large{\frac{1}{2}}\)mv² - \(\large{\frac{1}{2}}\)mv₀² = W

において、v₀ ⇒ v 、v ⇒ 0 としたものとみなせます。しかしこうすると上式の両辺は負となります。弾は減速したので、負の仕事を与えられたといえるからです。K が負とならなかったのは、K を、弾が外に与えた仕事と定義したからです。W は外から与えられた仕事と定義されてるので、K とは向き（正負）が逆になります。

このように、仕事に関する正負はとてもややこしいです。筆者もよく間違います。