運動エネルギー
運動している物体は何か他の物体に当たると、その物体を動かしたり変形させたりします。また、エネルギーとは「物体が持っている、仕事をする能力」であると、説明しました。だとすると、運動している物体はそれだけでエネルギーを持っていることになります。運動している物体が何か他の物体に当たったときに、動かしたり変形させたりすることができるからです。この運動している物体の持つエネルギーを運動エネルギーといいます。
直観的にいうと、運動の速さが速いほど他の物体への影響は大きそうです。また、物体の質量が大きければ大きいほど影響が大きそうです。運動エネルギーは、物体の速さや質量の大きさに関係ありそうだということが予想されます。
では実際に運動エネルギーの大きさを定義するには、どのように考えたらいいでしょうか。それは、運動している物体が他の物体に仕事をして、そのエネルギーを使い切るまでの仕事の量、とするのが妥当です。運動エネルギーを持った物体が他の物体にぶつかって止まったたときの、ぶつかる瞬間から止まる瞬間までの仕事の大きさです。この仕事の大きさを運動エネルギーの大きさとするのが妥当です。
左図は、粘土の塊にピストルで弾を撃ち込む場面です。弾が速いほど、弾が重いほど、その分、深くめり込みます。この弾の運動エネルギーを考えてみます。
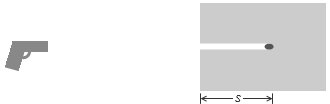弾の質量を m [kg]、弾の速さを v [m/s]、弾は s [m] 進んで止まり、減速するときの加速度は a [m/s2] で一定、弾が粘土を押す力は F [N] で一定、右向きが正、であるとします。
弾が粘土から受ける力は作用・反作用の法則より - F であり、弾の運動方程式を立てますと、
ma = - F
弾が減速していくときの運動は等加速度直線運動であり、等加速度直線運動の3式のうちの時間を含まない式を立てますと、
02 - v2 = 2as
∴ - v2 = 2as
∴ as = - \(\large{\frac{1}{2}}\)v2
仕事 W は、
W = Fs = - mas = - mas = - m(- \(\large{\frac{1}{2}}\)v2) = \(\large{\frac{1}{2}}\)mv2
であり、これが運動エネルギーです。
運動エネルギー
K = \(\large{\frac{1}{2}}\)mv2
単位は仕事と同じく [J] です。量記号は W ではなく K を使うことが多いです＊kinetic（運動の） から。
閉じる。
この式を解釈しますと、運動エネルギーは質量に比例し速さの2乗に比例する、といえます。ざっくりといえば、質量を持っているものは、動いていさえいればエネルギーを持っている、といえます。
なお今までは、物体が力を受けて移動したときに、そのとき受けた力と移動距離を掛け合わせて仕事の大きさを割り出しましたが、今回の粘土の場合は移動ではなく変形です。このような場合も仕事をされた、といいますが、その仕事の量は測定が困難です。しかし、ピストルの弾が与えた仕事については、力と移動距離がわかっているので測定できます。そして、粘土の受けた仕事の量と弾が与えた仕事の量は同じはずです。弾以外に仕事をしたものはいないのですから。
（『摩擦熱』の『運動エネルギー』もご参照ください。）
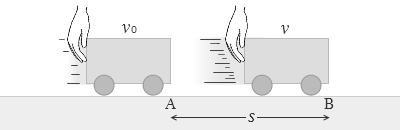始め v0 [m/s] で運動していた台車を、A地点からB地点までの間、手で力を加えることによって v [m/s] まで加速した場合を考えます。