気体分子の運動

気体分子運動論

容器に入れられた気体の圧力は、個々の気体分子の運動によって引き起こされるものです。無数の分子の絶え間ない壁への衝突が圧力の起源です。

微視的な分子の振る舞いから、巨視的な気体の圧力を導き出すとき、下記のように単純化されたモデルを考えます。

• 理想気体と同じく、分子には大きさが無く、分子間力も無い、とみなす。
• 分子には大きさが無いので、分子同士は衝突しないとみなす。
• 分子は全て同じ質量で、重力ははたらかないが、運動量や運動エネルギーはあるとみなす。
• 壁との衝突は弾性衝突（完全弾性衝突）で、壁と分子の間に摩擦は無いとみなす。
• 壁との衝突時以外は等速直線運動をするとみなし、平均するとあらゆる方向へ均等に（等方的に）運動するとみなす。

気体分子運動論から考える気体の圧力

立方体容器の１つの壁への衝突を考える

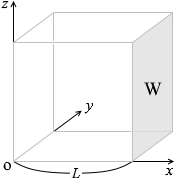1辺の長さ \(L\) [m]、体積 \(V\) [m³]（=\(L^3\)）の立方体の容器の中に、1個当たりの質量が \(m\) [kg] の気体分子が \(N\) 個入れられているとします。容器の各辺に合わせて \(x\)軸、\(y\)軸、\(z\)軸をとり、\(x\)軸に垂直な面を壁Wとします。

1個の分子が壁に与える力積

ある1個の分子が壁Wに衝突するときの速度を \(\vec{v}\) [m/s] とし、その \(x\)成分、\(y\)成分、\(z\)成分を \(v_x\) [m/s]、\(v_y\) [m/s]、\(v_z\) [m/s] とします。

壁Wへの衝突で変化するのは、 \(v_x\) だけです。\(v_y\) 、\(v_z\) は変化しません。＊
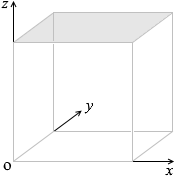
上面への衝突であれば、変化するのは \(v_z\) だけで、\(v_x\) 、\(v_y\) は変化しません。


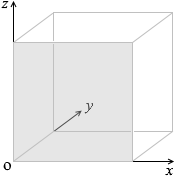
手前面への衝突であれば、変化するのは \(v_y\) だけで、\(v_x\) 、\(v_z\) は変化しません。 閉じる

つまり、3次元であるはずの壁Wへの衝突は、1次元として考えることができます。＊ 閉じる

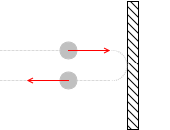\(x\)軸方向の分子の衝突前の運動量は \(mv_x\) で、衝突後の運動量は \(- mv_x\) ですから、衝突の際に分子が受けた力積は、

　　　\((- mv_x) - mv_x = - 2mv_x\)

です。逆に、壁Wが分子から受けた力積は \(2mv_x\) [N⋅s] です。

1個の分子が壁に与える平均の力

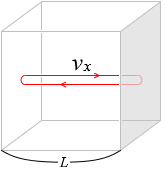ある1個の分子が \(x\)軸方向に \(t\)秒間に進む距離は \(v_xt\) [m] です。

分子が \(x\)軸方向に1往復するための距離は \(2L\) [m] です。

壁Wに衝突するのは 1往復に 1回です。

ということは \(t\)秒間に衝突する回数は \({\large\frac{v_xt}{2L}}\) 回です。＊ 例えば、
分子の \(x\)軸方向の速さが 8m/s であれば、6秒間に 48m 進みますが、容器の幅が 2m であれば往復で 4m であり、この分子は 6秒間に \({\large\frac{48}{4}}\) = 12回、衝突するということです。 閉じる

そして、1回の衝突で \(2mv_x\) の力積を与えるわけですから、

\(t\)秒間に与える力積は

　　　\(2mv_x × {\large\frac{v_xt}{2L}} = {\large\frac{m{v_x}^2t}{L}}\)

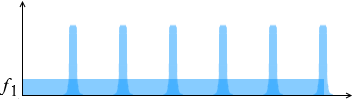
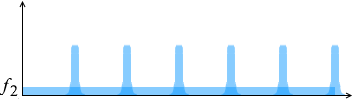
です。この量をグラフで表すと、

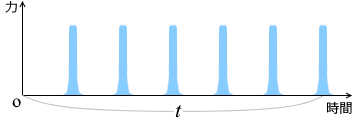左図のようになります。1つの山の面積が \(2mv_x\) [N⋅s] です。この山が \(t\)秒間当たり \({\large\frac{v_xt}{2L}}\) 個あります。合計で \({\large\frac{m{v_x}^2t}{L}}\) [N⋅s] の面積になるということです。

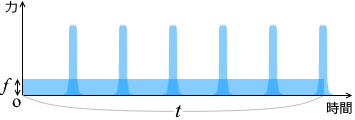この山を平らにならすと、その高さが平均の力となります。\({\large\frac{m{v_x}^2t}{L}}\) という面積を \(t\) で割ったものです。それが平均の力 \(f\) [N] です。（『撃力』参照）

　　　\(f = {\large\frac{m{v_x}^2t}{L}} ÷ \ t = {\large\frac{m{v_x}^2}{L}}\)

これが、1個の分子が壁Wに与える平均の力です。

\(N\)個の分子が壁に与える平均の力

今、この容器には \(N\) 個の気体分子が入れられているので、上記　\(f = {\large\frac{m{v_x}^2}{L}}\)　を \(N\)倍すれば、壁Wに掛かる力を求められると考えてしまいがちですが、これだと間違いです。

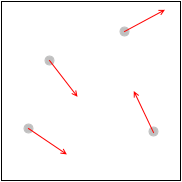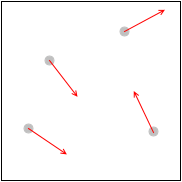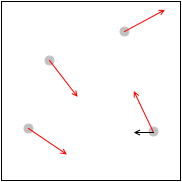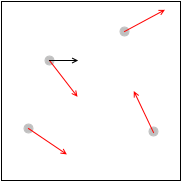\(v_x\) の大きさは分子によってそれぞれ違うのです。

＊ 「平均」については、2つの段階があります。
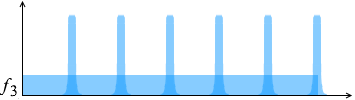
1つの分子について、複数回の衝突の山を平均化する、ということと、



　　・
　　・
　　・

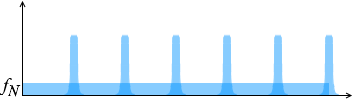
1~\(N\)個ある分子について、それらを平均化する、ということです。\(f\) といっても \(f_1\) から \(f_N\) まであります。 閉じる

ですから、\(N\)個ある分子の \({v_x}^2\) の平均を \(\overline{{v_x}^2}\) とし、これを \(N\)倍したものが正確な力ということになります。これを \(F\) [N] とおきます。

　　　\(F = {\large\frac{Nm{\overline{{v_x}^2}}}{L}}\)

壁Wへの圧力

壁Wへの圧力を \(p\) [Pa] としますと、圧力は力を面積で割ったものですから、

　　　\(p = {\large\frac{F}{L^2}} = {\large\frac{Nm{\overline{{v_x}^2}}}{L^3}}\)

であり、\(L^3 = V\) を代入すると、

　　　\(p = {\large\frac{Nm{\overline{{v_x}^2}}}{V}}\)　　……①

となります。

\(\overline{{v_x}^2}\) を \(\overline{{v}^2}\) で表す

\(\vec{v}\) の大きさ \(v\) を2乗した \(v^2\) は

　　　\(v^2 = {v_x}^2 + {v_y}^2 + {v_z}^2\)　＊ 三平方の定理です。



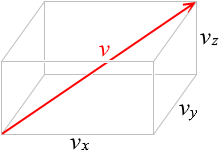
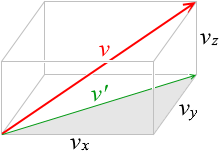　\(v'\)² = \(v_x\)² + \(v_y\)²

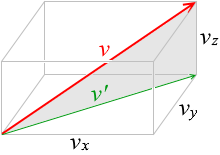　\(v\)² = \(v'\)² + \(v_z\)²

　∴　\(v\)² = \(v_x\)² + \(v_y\)² + \(v_z\)² 閉じる

と表されますので、その平均 \(\overline{{v}^2}\) も

　　　\(\overline{{v}^2} = \overline{{v_x}^2} + \overline{{v_y}^2} + \overline{{v_z}^2}\)

と表されます。そして、分子は等方的に動きますので　\(\overline{{v_x}^2} = \overline{{v_y}^2} = \overline{{v_z}^2}\)　です。つまり、

　　　\(\overline{{v}^2} = \overline{{v_x}^2} + \overline{{v_y}^2} + \overline{{v_z}^2} = \overline{{v_x}^2} + \overline{{v_x}^2} + \overline{{v_x}^2} = 3\overline{{v_x}^2}\)

であり、

　　　\(\overline{{v_x}^2} = {\large\frac{1}{3}}\overline{{v}^2}\)

です。これを①式に代入しますと、

となります。

この圧力は壁Wへの圧力というだけでなく、あらゆる面への圧力となっています。 パスカルの原理です。つまり、この圧力 \(p\) が、この容器内の気体の圧力です。

また、上式は

　　　\(p = {\large\frac{Nm{\overline{{v}^2}}}{3V}} = {\large\frac{2N}{3V}} × {\large\frac{1}{2}}m\overline{{v}^2}\)

と変形できますので、圧力 \(p\) は、気体分子の個数 \(N\) と気体分子の運動エネルギー \({\large\frac{1}{2}}mv^2\) の平均の値に比例し、体積 \(V\) に反比例する、と読み取れます。