気体分子の運動エネルギー
気体分子の平均運動エネルギー
『気体分子の運動』項で示した気体分子運動論による気体の圧力は
\(p = {\large\frac{Nm{\overline{{v}^2}}}{3V}}\)
と表されますが、この式は以下のように変形していくことができます。
⇔ \(pV = {\large\frac{1}{3}}Nm\overline{{v}^2}\)
⇔ \(pV = {\large\frac{2}{3}}⋅N⋅{\large\frac{1}{2}}m\overline{{v}^2}\)
この式の \(N\) というのは気体分子の個数です。今、気体の物質量が \(n\) [mol] であるとすると、アボガドロ定数 \(N_{\rm A}\) を用いて \(N = nN_{\rm A}\) と表せます。これを代入します。
⇔ \(pV = {\large\frac{2}{3}}⋅nN_{\rm A}⋅{\large\frac{1}{2}}m\overline{{v}^2}\)
理想気体の状態方程式 \(pV\) = \(nRT\) を左辺に代入します。
⇔ \(nRT = {\large\frac{2}{3}}⋅nN_{\rm A}⋅{\large\frac{1}{2}}m\overline{{v}^2}\)
⇔ \(RT = {\large\frac{2}{3}}⋅N_{\rm A}⋅{\large\frac{1}{2}}m\overline{{v}^2}\)
⇔ \({\large\frac{3}{2}}⋅{\large\frac{R\ }{N_{\rm A}}}⋅T = {\large\frac{1}{2}}m\overline{{v}^2}\)
⇔ \({\large\frac{1}{2}}m\overline{{v}^2} = {\large\frac{3}{2}}⋅{\large\frac{R\ }{N_{\rm A}}}⋅T\) ……①
この式のうち、\(R\) [J/(mol⋅K)] というのは気体定数であり、\(N_{\rm A}\) というのはアボガドロ定数であり、つまり \({\large\frac{R\ }{N_{\rm A}}}\) というのは定数です。これをボルツマン定数 19世紀のオーストリアの物理学者 ルートヴィッヒ・ボルツマン から といい、\(k\) とおきます。
\(\boldsymbol{k}\) = \({\large\frac{R\ }{N_{\rm A}}} = {\large\frac{8.31\ {\rm J/(mol⋅K)}}{6.02×10^{23}\ {\rm /mol}}}\) ≒ 1.38×10-23 J/K
この \(k\) を用いて上式を表すと以下のようになります。
気体分子の平均運動エネルギー
\(\boldsymbol{{\large\frac{1}{2}}m\overline{{v}^2} = {\large\frac{3}{2}}kT}\)
理想気体の気体分子1個の運動エネルギーは平均すると \({\large\frac{3}{2}}kT\) であるということです。\(k\) は定数ですから、これはすなわち、気体分子の運動エネルギーは絶対温度のみによって決まる、ということです。逆に言いますと、温度というのは運動エネルギーそのもの、ということです。
\({\large\frac{3}{2}}k = {\large\frac{3}{2}}\)×1.38×10-23 = 2.07×10-23 ですから上式は
\({\large\frac{1}{2}}m\overline{{v}^2}\) = 2.07×10-23\(T\)
ということになります。
たとえば、27℃ の気体における分子1個(単原子分子)の運動エネルギーは
2.07×10-23\(T\) = 2.07×10-23×(273+27) = 2.07×10-23×300 = 6.21×10-21 J
ということです。
気体分子の運動エネルギーは物質の種類によらないということでもあります。\(m\) が大きい種類の分子であればその分 \(\overline{{v}^2}\) が小さくなります。運動エネルギーは気体の種類に関係ありません。(下で説明するように、単原子分子か二原子分子かには関係があります)
エネルギー等配分の法則
また、気体分子は等方的に動きますので \(\overline{{v_x}^2} = \overline{{v_y}^2} = \overline{{v_z}^2}\) であり、\(\overline{{v}^2} = \overline{{v_x}^2} + \overline{{v_y}^2} + \overline{{v_z}^2}\) でありますから、上式は
\({\large\frac{1}{2}}m\overline{{v}^2} = {\large\frac{1}{2}}m\overline{{v_x}^2} + {\large\frac{1}{2}}m\overline{{v_y}^2} + {\large\frac{1}{2}}m\overline{{v_z}^2} = {\large\frac{3}{2}}kT\)
とも書き表され、すなわち、
\({\large\frac{1}{2}}m\overline{{v_x}^2} = {\large\frac{1}{2}}kT\) 、\({\large\frac{1}{2}}m\overline{{v_y}^2} = {\large\frac{1}{2}}kT\) 、\({\large\frac{1}{2}}m\overline{{v_z}^2} = {\large\frac{1}{2}}kT\)
であるといえます。\(x\)方向にも \(y\)方向にも \(z\)方向にも均等にエネルギーが分配されます。
これは1個の原子からなる分子、単原子分子の場合の話です。ヘリウム(He)やネオン(Ne)やアルゴン(Ar)などの気体です。
水素(H2)や窒素(N2)や酸素(O2)など、2個の原子からなる二原子分子では、分子のエネルギー \(U\) が
\(U = {\large\frac{1}{2}}kT×5 = {\large\frac{5}{2}}kT\)
であったり、さらに、
水(H2O)など、3個以上の原子からなる多原子分子(非直線型)では
\(U = {\large\frac{1}{2}}kT×6 = 3kT\)
であったりなど、\({\large\frac{1}{2}}kT\) の整数倍になっていたりします。このことをエネルギー等分配の法則といいます。この原理は高校生にはちょっと難しいです。大学に行ってから詳しく学びます。
大雑把な説明をしますと、
3次元空間において、運動の方向は \(x\)方向、\(y\)方向、\(z\)方向とありますが、これは並進運動のみを考えた場合です。もし、物体に大きさがあるなら回転運動も考えるべきで、そうすると \(x\)軸を中心とした回転方向、\(y\)軸を中心とした回転方向、\(z\)軸を中心とした回転方向があり(飛行機の運動でいうところの ロール と ヨー と ピッチ )、運動の方向は全部で6個となります。
この世が1次元(\(x\)軸)であれば、ポンと放り投げられた(大きさの無い)分子は \(x\)方向にのみ運動します。これを自由度 1 とカウントします。暴れ回れる自由度が 1 です。
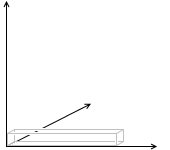
この世が2次元(\(x\)軸、\(y\)軸)であれば、ポンと放り投げられた分子は \(x\)方向、\(y\)方向に運動します。これを自由度 2 とカウントします。
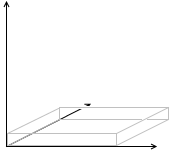
この世が3次元(\(x\)軸、\(y\)軸、\(z\)軸)であれば、ポンと放り投げられた分子は \(x\)方向、\(y\)方向、\(z\)方向に運動します。これを自由度 3 とカウントします。
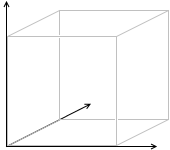
もし、分子が二原子分子  であれば、これは大きさがあるということになり(長さがあるが太さが無いと考える)、回転についても考慮しなければならなくなり、つまり、回転運動エネルギーも考えなければなりません。(物体は回転しているだけでエネルギーを持ちます)
であれば、これは大きさがあるということになり(長さがあるが太さが無いと考える)、回転についても考慮しなければならなくなり、つまり、回転運動エネルギーも考えなければなりません。(物体は回転しているだけでエネルギーを持ちます)
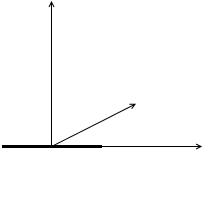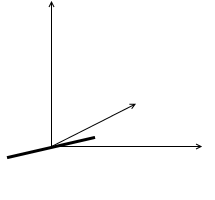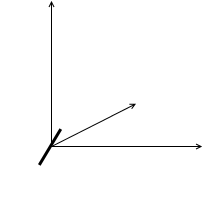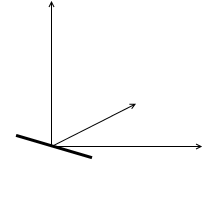 ヨー方向の回転
ヨー方向の回転
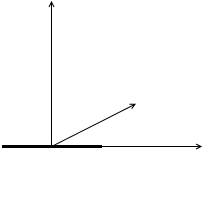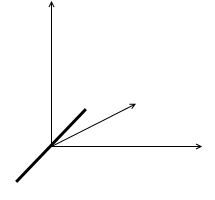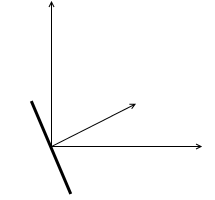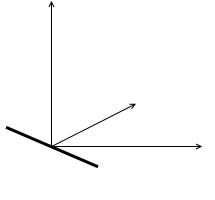 ピッチ方向の回転
ピッチ方向の回転
ロール方向の回転はありません。回転していると考えても、太さが無いのでエネルギーを持ちません。
二原子分子では、ヨー回転で自由度 1 、ピッチ回転で自由度 1 、総計の自由度が 5 であると考えます。
三原子分子は、二酸化炭素(CO2)などの直線型  では自由度が 5 、水(H2O)などの非直線型
では自由度が 5 、水(H2O)などの非直線型  では、ロール方向の回転が加わり、自由度が 6 となります。
では、ロール方向の回転が加わり、自由度が 6 となります。
自由度 1 につき \({\large\frac{1}{2}}kT\) の運動エネルギーが割り当てられます。\(k\) というのは 1.38×10-23 という数値ですから、\({\large\frac{1}{2}}kT\) はすなわち 0.69×10-23\(T\) という量です。27℃であれば \(T\)=300 K ですから、0.69×10-23×300 = 207×10-23 J です。
たとえば、あり得ない仮定ですが、
27℃ の1次元の箱に1個の分子を放り込めば、そのエネルギーは 207×10-23 J です。
27℃ の2次元の箱に1個の二原子分子を放り込めば、自由度は \(x\)方向、\(y\)方向、ヨー回転方向の 3 で、そのエネルギーは 3×207×10-23 J です。
6つある運動方向のうちのどこかだけにエネルギーが偏ることが無い、というのがエネルギー等分配の法則です。
また、自由度の小さい気体と自由度の大きい気体では、同じ 1℃ の上昇でも、エネルギーの量が違うということであり、自由度の小さい気体は少しの熱で簡単に温度が上昇します。逆に言うと、自由度の大きい気体は同じ 1℃ の上昇でも、たくさんの熱を含有します。自由度の大小は熱容量の大きさに関係してきます。
モル質量
分子 602000000000000000000000個 の質量をモル質量といいます。1mol の分子の質量です。大雑把にいえば分子量のことです。厳密な定義については化学の教科書を見てください。量記号は \(M\) を用います 質量に使われる量記号 \(m\) と同じく mass から 。単位は [g/mol] です [kg/mol] ではなく [g/mol] です。物理的には [kg/mol] の方が自然ですが、化学の都合で [g/mol] となってます。 。水素分子(H2) 602000000000000000000000個 の質量は 2g です。
ある気体分子1個の質量を \(m\) [kg] とすると、1mol (=\(N_{\rm A}\)個) の質量は \(mN_{\rm A}\) [kg] です。
この気体分子の分子量を \(M\) とすると、1mol (=\(N_{\rm A}\)個) の質量は \(M\) [g] です。これは \(M\)×10-3 [kg] です。
つまり、
\(mN_{\rm A}\) = \(M\)×10-3 ……②
です。
2乗平均速度
①式を変形してから②式を代入します。
\({\large\frac{1}{2}}m\overline{{v}^2} = {\large\frac{3}{2}}⋅{\large\frac{R\ }{N_A}}⋅T\)
⇔ \(m\overline{{v}^2} = 3⋅{\large\frac{R\ }{N_A}}⋅T\)
⇔ \(\overline{{v}^2} = {\large\frac{3RT}{\color{#090}{mN_A}}}\)
∴ \(\overline{{v}^2} = {\large\frac{3RT}{\color{#909}{M×10^{-3}}}}\)
平方根をとりますと、
\(\sqrt{\overline{{v}^2}} = \sqrt{{\large\frac{3RT}{M×10^{-3}}}}\)
となり、この \(\sqrt{\overline{{v}^2}}\) を2乗平均速度といいます。
2乗平均速度
\(\boldsymbol{\sqrt{\overline{{v}^2}} = \sqrt{{\large\frac{3RT}{M×10^{-3}}}}}\)
この式をよく見てみますと、\(R\) は定数ですから、2乗平均速度というのは絶対温度と分子量によって決まるということが分かります。温度が高い方が速度が速く、分子量が大きいほど(重いほど)速度が遅いです。
この2乗平均速度というのは単純な平均速度とは微妙に違います
たとえば、
1, 2, 3, 4, 5 を単純に平均すると 3 です。
1, 2, 3, 4, 5 を2乗してから平均して平方根をとると、
12, 22, 32, 42, 52 → 1, 4, 9, 16, 25 → 総和は 55 → 5で割ると 11 → 平方根をとると \(\sqrt{11}\) ≒ 3.32 となります。
3 より大きくなります。2乗平均速度は運動エネルギー \({\large\frac{1}{2}}mv^2\) に関係する量なので 4 や 5 などの大きい数値が優遇され、平均が大きくなります。交流の実効値にちょっと似ています。
あと、
速度はベクトルである、と考えて平均をとると 0 になってしまいます。たとえば、-3, -2, -1, 0, 1, 2, 3 を単純に平均すると 0 です。
「平均」にはいろいろあります。
。単純な平均速度は運動エネルギーと直接は関係ありません。2乗平均速度であれば、運動エネルギーと関係があるし、温度や分子量とも直接関係があり、速さとして重要な目安となります。
測定が容易な量の組み合わせによって計算して導き出すこともできます。
| 分子量 | \(\sqrt{\overline{{v}^2}}\) [m/s] | |
|---|---|---|
| 水素(H2) | 2.0 | 1.8 ×103 |
| ヘリウム(He) ヘリウムの音速がとても速いのは、ヘリウム分子の2乗平均速度が速いのと関連があります。気体分子の運動スピードが速ければ、音の波が伝わる速さも当然速くなります。 | 4.0 | 1.3 ×103 |
| ネオン(Ne) | 20 | 0.58×103 |
| 窒素(N2) | 28 | 0.49×103 |
| 酸素(O2) | 32 | 0.46×103 |
| 二酸化炭素(CO2) | 44 | 0.39×103 |
軽い分子ほどスピードが速くなってます。
\(R\) というのは 8.31 という数値であり、上の表においては絶対温度は \(K\) = 273 です。すなわち、
\(\sqrt{\overline{{v}^2}} = \sqrt{{\large\frac{3RT}{M×10^{-3}}}} = \sqrt{{\large\frac{3×8.31×273}{M×10^{-3}}}} ≒ \sqrt{{\large\frac{6781}{M×10^{-3}}}} ≒ \sqrt{{\large\frac{6.781×10^6}{M}}}\)
≒ 2.60×103×\(\sqrt{{\large\frac{1}{M}}}\)
です。
水素:2.60×103×\(\sqrt{{\large\frac{1}{2.0}}}\) ≒ 2.60×103×0.707 ≒ 1.84×103
ヘリウム:2.60×103×\(\sqrt{{\large\frac{1}{4.0}}}\) = 2.60×103×0.5 = 1.30×103
ネオン:2.60×103×\(\sqrt{{\large\frac{1}{20}}}\) ≒ 2.60×103×0.223 ≒ 0.581×103
窒素:2.60×103×\(\sqrt{{\large\frac{1}{28}}}\) ≒ 2.60×103×0.189 ≒ 0.491×103
酸素:2.60×103×\(\sqrt{{\large\frac{1}{32}}}\) ≒ 2.60×103×0.177 ≒ 0.460×103
二酸化炭素:2.60×103×\(\sqrt{{\large\frac{1}{44}}}\) ≒ 2.60×103×0.151 ≒ 0.391×103