ドップラー効果の式
観測者が動く場合
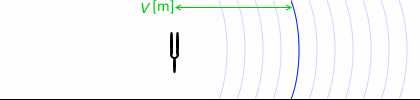
音源(Source)が止まっていて観測者(Observer)が動いている場合の、ドップラー効果による振動数の変化について、考えてみます。
音速を \(V\) [m/s]、音源が発する音波の振動数を \(f_0\) [Hz] エフゼロ 、波長を \(λ_0\) [m] ラムダゼロ 、観測者の速さを \(v_{\rm o}\) [m/s] ヴイオー。Observer の O です。 とします。
\(v = fλ\) という関係があるので \({\color{orange}λ_0 = {\large\frac{V}{f_0}}}\) です。

観測者が音源から遠ざかる場合の、観測者から見た音波の相対速度は \(V - v_{\rm o}\) です たとえば \(V\)=340m/s、\(v_{\rm o}\)=100m/s なら、相対速度は 240m/s です。 。よって、観測者が感知する振動数 \(f_1\) [Hz] は、(\(v = f λ\) の関係より)
\(f_1 = {\large\frac{V-v_{\rm o}}{λ_0}}\) \({\color{orange}λ_0 = {\large\frac{V}{f_0}}}\) を代入して
\(= {\large\frac{V-v_{\rm o}}{\frac{V}{f_0}}}\)
\(= {\large\frac{V-v_{\rm o}}{V}}f_0\)
たとえば \(V\)=340m/s、\(v_{\rm o}\)=100m/s なら、
\(f_1 = {\large\frac{V-v_{\rm o}}{V}}f_0 = {\large\frac{340-100}{340}}f_0 = {\large\frac{240}{340}}f_0 ≒ 0.7f_0\)
観測者が感知する振動数は、音源の振動数の 0.7倍くらいです。音が低くなるということです。
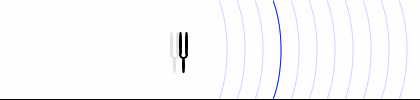
観測者が音源に近づいていく場合の、観測者から見た音波の相対速度は \(V + v_{\rm o}\) です たとえば \(V\)=340m/s、\(v_{\rm o}\)=100m/s なら、相対速度は 440m/s です。 。上と同じように計算すると、
\(f_1{'} = {\large\frac{V+v_{\rm o}}{V}}f_0\)
たとえば \(V\)=340m/s、\(v_{\rm o}\)=100m/s なら、
\(f_1{'} = {\large\frac{V+v_{\rm o}}{V}}f_0 = {\large\frac{340+100}{340}}f_0 = {\large\frac{440}{340}}f_0 ≒ 1.3f_0\)
観測者が感知する振動数は、音源の振動数の 1.3倍くらいです。音が高くなるということです。
ですが、この式は、音源から観測者への向きを正とし、\(v_{\rm o}\) は正の値も負の値も持つ、とすれば、観測者が音源から遠ざかる場合の式の \(V - v_{\rm o}\) の \(v_{\rm o}\) の部分に \(- v_{\rm o}\) を代入して \(V - (- v_{\rm o}) = V + v_{\rm o}\) としたことに相当します。
音源が動く場合
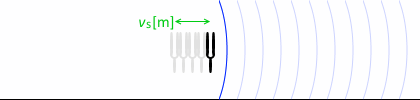
次に、音源が動いて観測者が止まっている場合の、ドップラー効果による振動数の変化について、考えてみます。
音速を \(V\)、音源が発する音波の振動数を \(f_0\) 、音源が動いていない場合の波長を \(λ_0\) 、音源の動く速さを \(v_{\rm s}\)
ヴイエス。
Source の S です。
とします。
音源の前方では波長が縮むわけですが、音源の発する振動数は音源が止まっていようと動いていようと変わらないので \(f_0\) 。音波は \(V\) で進んでいて音源は \(v_{\rm s}\) で進んでいるので相対速度は \(V - v_{\rm s}\) 。この2つの量を \(v = fλ\) の関係式に代入して、動く音源が前方に作る音波の波長 \(λ_2\) を求めると、
\({\color{orange}λ_2 = {\large\frac{V-v_{\rm s}}{f_0}}}\)
音源が1秒間に送り出す波の数は \(f_0\) 個で、
音波が1秒間に進む距離というのは \(V\) [m] で、
音源が1秒間に進む距離というのは \(v_{\rm s}\) [m] なので、
この1秒間の内の1個目から\(f_0\)個目までの長さは \(V - v_{\rm s}\) [m] 。


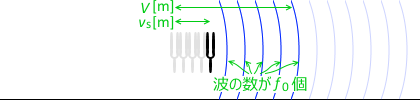
ということは、波1個当たりの長さは、
\({\large\frac{V-v_{\rm s}}{f_0}}\) [m] で、
波1個当たりの長さというのは波長のこと。
となります。このことは、
\(v_{\rm s}\) で動く音源が前方に作る音波の波長というのは、
音源が止まっていて、音波のスピードが \(V - v_{\rm s}\) である場合の波長と同じ、
という意味でもあります。
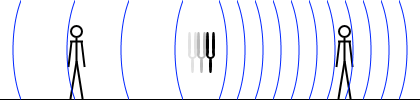
このような音波の波長を、止まっている観測者が感知したときの振動数 \(f_2\) は、(\(v = fλ\) の関係より)
\(f_2 = {\large\frac{V}{λ_2}}\) \({\color{orange}λ_2 = {\large\frac{V-v_{\rm s}}{f_0}}}\) を代入して
\(= {\large\frac{V}{\frac{V-v_{\rm s}}{f_0}}}\)
\(= {\large\frac{V}{V-v_{\rm s}}}f_0\)
たとえば \(V\)=340m/s、\(v_{\rm s}\)=100m/s なら、
\(f_2 = {\large\frac{V}{V-v_{\rm s}}}f_0 = {\large\frac{340}{340-100}}f_0 = {\large\frac{340}{240}}f_0 ≒ 1.4 f_0\)
観測者が感知する振動数は、音源の振動数の 1.4倍くらいです。音が高くなるということです。
音源の後方では波長が伸びるわけですが、このときの波長 \(λ_2{'}\) は、上と同じように考えて、
\({\color{orange}λ_2{'} = {\large\frac{V+v_{\rm s}}{f_0}}}\)
となりますので、止まっている観測者が感知したときの振動数 \(f_2{'}\) は、上と同じように計算して、
\(f_2{'} = {\large\frac{V}{V+v_{\rm s}}}f_0\)
たとえば \(V\)=340m/s、\(v_{\rm s}\)=100m/s なら、
\(f_2{'} = {\large\frac{V}{V+v_{\rm s}}}f_0 = {\large\frac{340}{340+100}}f_0 = {\large\frac{340}{440}}f_0 ≒ 0.77 f_0\)
観測者が感知する振動数は、音源の振動数の 0.77倍くらいです。音が低くなるということです。
ですが、この式は、音源から観測者への向きを正とし、\(v_{\rm s}\) は正の値も負の値も持つ、とすれば、音源の前方の場合の式の \(V - v_{\rm s}\) の \(v_{\rm s}\) の部分に \(-v_{\rm s}\) を代入して \(V -(- v_{\rm s}) = V + v_{\rm s}\) としたことに相当します。
また、分子の \(V\) ですが、ここを \(V - v_{\rm s}\) などとすると間違いです。音波は風など吹かない限り速さは変わりません。
音源も観測者も動く場合
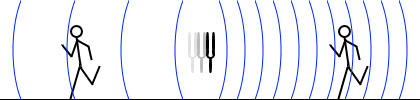
音源が止まっていて観測者(Observer)が動いている場合の振動数は、
\({\color{green}f_1 = {\large\frac{V-v_{\rm o}}{V}}f_0}\) ……①
で、音源(Source)が動いて観測者が止まっている場合の振動数は、
\({\color{purple}f_2 = {\large\frac{V}{V-v_{\rm s}}}f_0}\) ……②
であるわけなので、音源も観測者も両方動く場合の振動数 \(f\) は、2つを合わせて、
\(f = {\large\frac{V-v_{\rm o}}{V-v_{\rm s}}}f_0\)
となります。この式は、①式の \(f_0\) のところが \(f_2\) になったものとして(つまり①式に②式を代入して)、
\(f = {\color{green}{\large\frac{V-v_{\rm o}}{V}}f_0} = {\color{green}{\large\frac{V-v_{\rm o}}{V}}\color{purple}{f_2}}\) = \({\color{green}{\large\frac{V-v_{\rm o}}{V}}}×{\color{purple}{\large\frac{V}{V-v_{\rm s}}}f_0} = {\large\frac{V-v_{\rm o}}{V-v_{\rm s}}}f_0\)
 これが、
これが、
 こうなった、と考える。
こうなった、と考える。
と考えてもいいですし、②式の \(f_0\) のところが \(f_1\) になったものとして(つまり②式に①式を代入して)、
\(f = {\color{purple}{\large\frac{V}{V-v_{\rm s}}}f_0}\) = \({\color{purple}{\large\frac{V}{V-v_{\rm s}}}}\color{green}{f_1}\) = \({\color{purple}{\large\frac{V}{V-v_{\rm s}}}}×{\color{green}{\large\frac{V-v_{\rm o}}{V}}f_0} = {\large\frac{V-v_{\rm o}}{V-v_{\rm s}}}f_0\)
 これが、
これが、
 こうなった、と考える。
こうなった、と考える。
と考えてもいいです。
ドップラー効果
\(\boldsymbol{f = {\large\frac{V-v_{\rm o}}{V-v_{\rm s}}}f_0}\)
\(f\):観測者が感知する振動数 \(V\):音速 \(f_0\):音源の振動数
\(v_{\rm o}\):観測者の速度 \(v_{\rm s}\):音源の速度 音源から観測者への向きを正とする
この公式は分母と分子を間違えやすいので「オトブンノヒト」と覚えてください。あと、\(- v\) とするか \(+ v\) とするか、とても間違えやすいです。ドップラー効果の原理に照らし合わせて、この場合は振動数が大きくなるはず、この場合は振動数が小さくなるはず、と直感を大事にして慎重に判断してください。
また、ドップラー効果は試験等では音速は 340m/s として出題されることが多いので、
\(f = {\large\frac{340-v_{\rm o}}{340-v_{\rm s}}}f_0\)
と覚えてしまってもいいかもしれません。