ドップラー効果は正負がややこしい
前項で示したように、ドップラー効果の式は、
\(f = {\large\frac{V-v_{\rm o}}{V-v_{\rm s}}}f_0\)
というものですが、\(v_{\rm o}\) と \(v_{\rm s}\) の正負の決め方が、
「音源から観測者への向きを正とする」
というものでした。これがちょっとややこしくて間違いやすいです。
たとえば、\(V\) が 340m/s で、\(v_{\rm o}\) 、\(v_{\rm s}\) が 100m/s の場合、以下のようなパターンがあります。
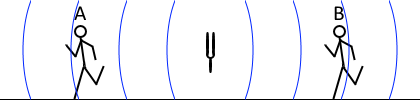
\(f_{\rm A} = {\large\frac{340-100}{340}}f_0\) \(f_{\rm B} = {\large\frac{340+100}{340}}f_0\)
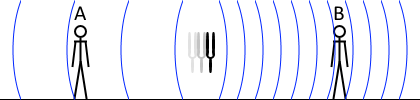
\(f_{\rm A} = {\large\frac{340}{340+100}}f_0\) \(f_{\rm B} = {\large\frac{340}{340-100}}f_0\)
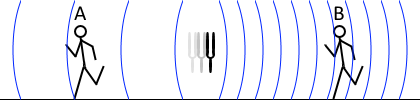
\(f_{\rm A} = {\large\frac{340-100}{340+100}}f_0\) \(f_{\rm B} = {\large\frac{340+100}{340-100}}f_0\)
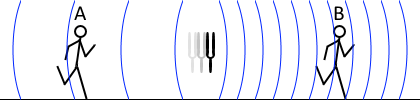
\(f_{\rm A} = {\large\frac{340+100}{340+100}}f_0\) \(f_{\rm B} = {\large\frac{340-100}{340-100}}f_0\)
「音源から観測者への向きを正とする」と覚えてもどうしても間違えてしまいます。『ドップラー効果１』で説明した原理をしっかり理解して、「オトブンノヒト」と覚えて、分母（分子）に足す（引く）と、振動数は大きくなるのか、小さくなるのかをよく考えてください。
音速に近い速さで動くとき
次に、ドップラー効果をより深く理解してもらうために、音源や観測者が音速に近い速さで動く場合について説明します。\(v_{\rm o} = v_{\rm s} =\) 339m/s とします。
上で挙げた１番目のパターン
\({\color{red}f_{\rm A}} = {\large\frac{340-339}{340}}f_0 = {\large\frac{1}{340}}f_0\) ほぼ 0 です。音速とまったく同じスピード（マッハ1）で進むと音を感じなくなります。音波は鼓膜を揺らしません。
かといって、マッハ1で飛ぶ飛行機の中にいるパイロットは無音にはならないと思います。エンジン音は機体を伝わり、骨を伝わり、脳に届くはずです。
\({\color{red}f_{\rm B}} = {\large\frac{340+339}{340}}f_0 ≒ 2f_{\rm 0}\) ただ2倍になるだけです。1オクターブ高い音になります。
上で挙げた２番目のパターン
\({\color{red}f_{\rm A}} = {\large\frac{340}{340+339}}f_0 ≒ {\large\frac{1}{2}}f_{\rm 0}\) ただ半分になるだけです。1オクターブ低い音になります。
\({\color{red}f_{\rm B}} = {\large\frac{340}{340-339}}f_0 = 340f_{\rm 0}\) なんと340倍です。もし \(v_{\rm s}\) が 339m/s でなく 339.9m/s なら3400倍です。
これは実際には、
このようになるということです。
さらに描けば、
このようになるということです。移動する音源の先頭で全ての音波が重なり合います。
大音響が発生します。ソニックブームといいます。通常ジェット機はソニックブームが発生しないようマッハ1に達しない速度で飛んでいます。
発生原理から言ってソニックブームを抑えるのはなかなか難しく、それゆえ旅客機のこれ以上の速度向上は望めません。ソニックブーム Wikipedia 参照
波の発生源の移動する速さが、波の速さを超えることも起こり得ます。
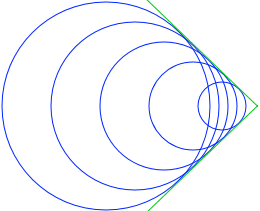波の様子は左図のようになります。
共通する接線の部分に大きな波ができます。衝撃波といいます。ソニックブームも衝撃波の一種です。
モーターボートは水面波の速さを簡単に超えます。ですので、どうしても衝撃波が発生してしまいます。
手漕ぎボートでいちゃついてるカップルを見つけたモーターボートの操縦士は、わざと高速で間近を通過し衝撃波を浴びせたりします。