ドップラー効果の原理
ドップラー効果
電車に乗っているとき、踏み切りのカンカンカンという警報音を聞くと、通り過ぎる前は高い音に聞こえ、通り過ぎた後は低い音に聞こえます。また道を歩いていて、救急車がサイレンを鳴らして近づいてくるとき、音がだんだん大きくなるとともに音が高い音に聞こえ、救急車が通り過ぎたとたんに音が低い音に聞こえます。このように観測者と音源が互いに近づいたり遠ざかったりするときに音の高さが変わることをドップラー効果 19世紀のオーストリアの物理学者クリスチャン・ドップラーが発見しました といいます。
音の感知
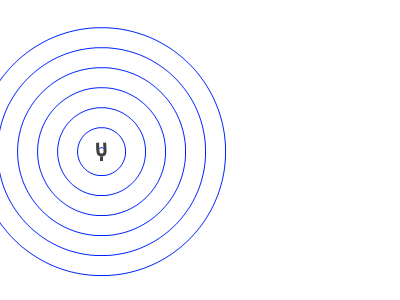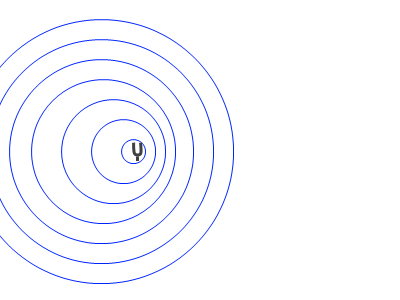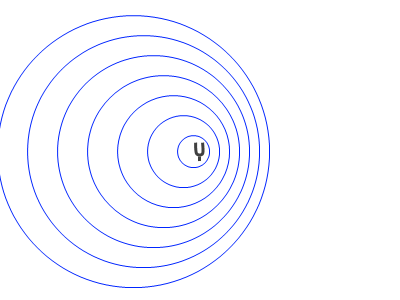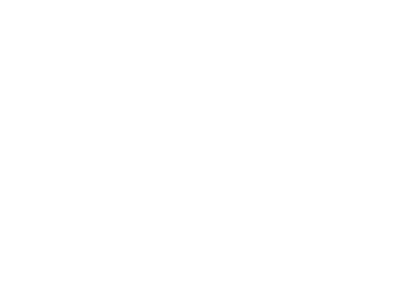
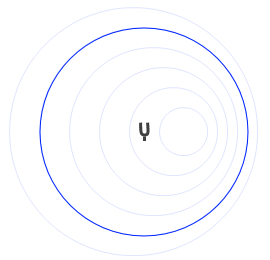
左図は音を感知している様子を表したアニメーションです。
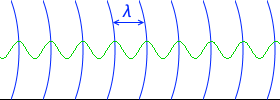青線の間隔は波長の大きさを表しています。
赤色の点滅の速さは振動数の大きさを表しています。点滅が速いということは振動数が大きい（音が高い）ということです。
観測者が動くと振動数が変わる
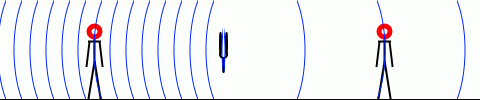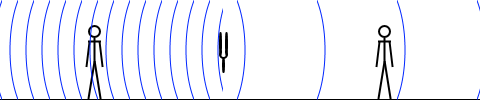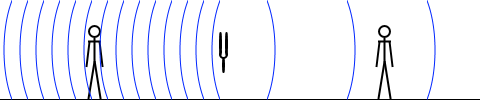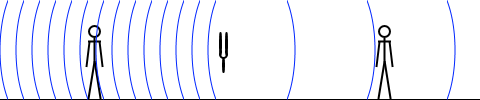
観測者が動くと、観測者が感知する振動数が変わります。観測者が音波と同じ方向に進むと赤色の点滅スピードが落ちます。観測者が音波と逆の方向に進むと赤色の点滅スピードが上がります。立ち止まっている観測者にとっては振動数は変わりません。
振動数が変化するのは音波と観測者の相対速度が変わったためです。
このことは、観測者が止まっていて、風が吹いて、音波全体が流されたことと同等です。風が吹くと、風上に向かう音波は遅くなり、風下に向かう音波は速くなります。
上図は音源も風に流されている場面の図ですが、普通、音源というものは風が吹いていても固定されていることが多いです。そのような場合は左図のようになります。
この場合のドップラー効果の式を表すと、
\(f = {\large\frac{(V+u) - v_{\rm o}}{(V+u) - v_{\rm s}}}f_0\)
という感じになります。
\(u\) が風の速度です。\(u\) は正の値も負の値も取り、音源から観測者への向きを正とします。
\(v_{\rm o} = 0\) 、\(v_{\rm s} = 0\) なら、
\(f = {\large\frac{(V+u)-0}{(V+u)-0}}f_0 = f_0\)
という感じです。音の高さは変わらないということです。
\(f = {\large\frac{v}{λ}}\) の式でいうと、\(v\) が半分のとき \(λ\) も半分、\(v\) が2倍のとき \(λ\) も2倍、で結局 \(f\) の大きさは変わらない、というようなことです。
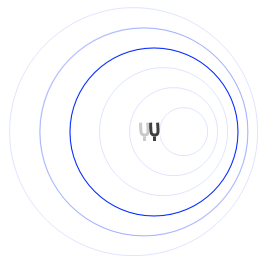
音源が動くと振動数が変わる
音源が動くと、その前方では波長が縮み、後方では波長が伸びます。前方では振動数が高くなり、後方では振動数が低くなるのです。
このとき、音波（青線の1本1本）の進む速さは変化していません。風でも吹かない限り音波は加速しません。音源が加速しても音波は加速しません。
前方において、波の間隔が狭まったのは、波の発生源の位置が動いたためです。
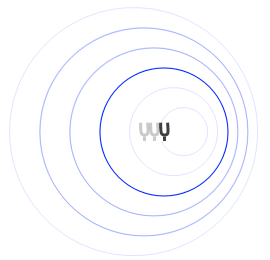
各波の発生源の位置を意識してください。
左図のような青波の発生源の位置。
左図のような青波の発生源の位置。
左図のような青波の発生源の位置。
音波のスピードがUPしたから波長が縮んだのではなく、発生源の位置が動いたから波長が縮んだのです。