波面
水面に石を投げ込むと円形の波が広がっていきます。このときの波というものは、水面の各地点の内の、山なら山、谷なら谷の点(同位相の点)を結んだ線(3次元的にいえば面)です。このような面を波面といいます。波の進行方向と波面とは常に垂直です。
波面が平面のものを平面波といい、波面が球面状(同心円状)のものを球面波といいます。円形に広がっていく波も球面波の一種です(立体的な球面を平面で分断すると円になります)。球面はどんどん大きくなると平面に近くなるので(地球の地表が平面に感じられるのと同じように)、波源から遠く離れた球面波は平面波とみなせます。
ホイヘンスの原理
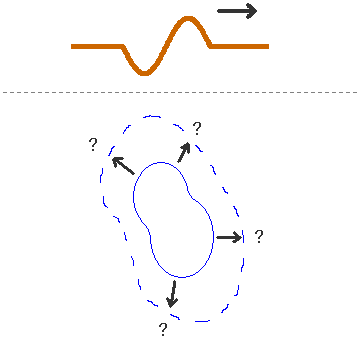 直線状(1次元)の媒質を進んでいく波の方向は前か後ろかでしたが、水面や空中(2次元、3次元)における波の方向や形についてはそう単純ではありません。このときに使う考え方がホイヘンスの原理です
17世紀のオランダの物理学者クリスティアーン・ホイヘンスが発見しました
。
直線状(1次元)の媒質を進んでいく波の方向は前か後ろかでしたが、水面や空中(2次元、3次元)における波の方向や形についてはそう単純ではありません。このときに使う考え方がホイヘンスの原理です
17世紀のオランダの物理学者クリスティアーン・ホイヘンスが発見しました
。
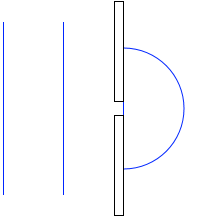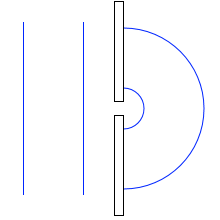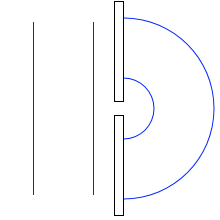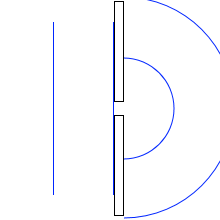 水面を進む平面波が防波堤を過ぎるとその先で球面波となります。この現象から類推して、ホイヘンスは素元波というものを考え、次のような理論を打ち立てました。
水面を進む平面波が防波堤を過ぎるとその先で球面波となります。この現象から類推して、ホイヘンスは素元波というものを考え、次のような理論を打ち立てました。
 ”ある瞬間における波面上の各点が新しい波源となって、球面波(素元波)が生じ、これらの素元波に共通に接する面が次の瞬間の波面となる。”
”ある瞬間における波面上の各点が新しい波源となって、球面波(素元波)が生じ、これらの素元波に共通に接する面が次の瞬間の波面となる。”
左図の赤色の波が素元波です。素元波を小刻みに描くほど正確な波面の図が得られます。
 平面波の場合であれば、素元波を小刻みに描いても粗く描いても得られる波面の図に変わりはありません。どっちみち平面です。
平面波の場合であれば、素元波を小刻みに描いても粗く描いても得られる波面の図に変わりはありません。どっちみち平面です。
 ホイヘンスの原理により、S字状に配列した波源から出る波がS字の形を保ち続けることはできないことがわかります。
ホイヘンスの原理により、S字状に配列した波源から出る波がS字の形を保ち続けることはできないことがわかります。
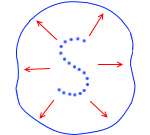 波は放射状に広がっていきます。波源から十分離れた所では円形に近くなります。このことは『電気力線』や『磁力線』に近いものがあります。
波は放射状に広がっていきます。波源から十分離れた所では円形に近くなります。このことは『電気力線』や『磁力線』に近いものがあります。
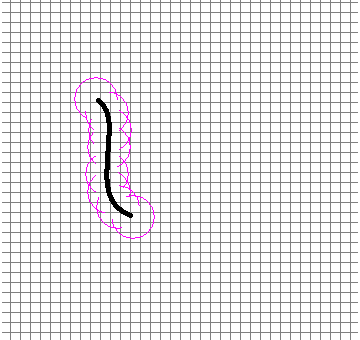 ホイヘンスの原理は当たり前といえば当たり前で、例えば波をよく伝える柔軟なネットがあって、その上にいびつな形の鉄の棒を落としたとき、どのような波面になるかを考えると、それは各点から等距離にコンパスで無数の半円を描いてつなげたものになるはずです。地図において日本の領海線を引くような作業です。
ホイヘンスの原理は当たり前といえば当たり前で、例えば波をよく伝える柔軟なネットがあって、その上にいびつな形の鉄の棒を落としたとき、どのような波面になるかを考えると、それは各点から等距離にコンパスで無数の半円を描いてつなげたものになるはずです。地図において日本の領海線を引くような作業です。
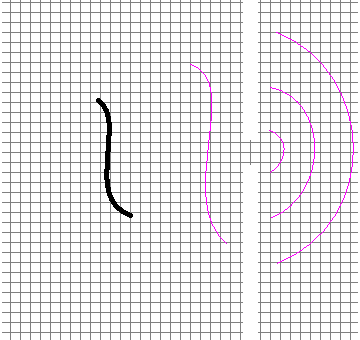 もしネットに途切れ目があればこれは水面における防波堤のような役割になり、左図のような波面ができるはずです。
もしネットに途切れ目があればこれは水面における防波堤のような役割になり、左図のような波面ができるはずです。
 水面を進む平面波が防波堤を過ぎるとその先で球面波となります。この現象から類推して、ホイヘンスは素元波というものを考え、次のような理論を打ち立てました。
水面を進む平面波が防波堤を過ぎるとその先で球面波となります。この現象から類推して、ホイヘンスは素元波というものを考え、次のような理論を打ち立てました。 ”ある瞬間における波面上の各点が新しい波源となって、球面波(素元波)が生じ、これらの素元波に共通に接する面が次の瞬間の波面となる。”
”ある瞬間における波面上の各点が新しい波源となって、球面波(素元波)が生じ、これらの素元波に共通に接する面が次の瞬間の波面となる。”  平面波の場合であれば、素元波を小刻みに描いても粗く描いても得られる波面の図に変わりはありません。どっちみち平面です。
平面波の場合であれば、素元波を小刻みに描いても粗く描いても得られる波面の図に変わりはありません。どっちみち平面です。 ホイヘンスの原理により、S字状に配列した波源から出る波がS字の形を保ち続けることはできないことがわかります。
ホイヘンスの原理により、S字状に配列した波源から出る波がS字の形を保ち続けることはできないことがわかります。 波は放射状に広がっていきます。波源から十分離れた所では円形に近くなります。このことは『
波は放射状に広がっていきます。波源から十分離れた所では円形に近くなります。このことは『