位相=タイミング
位相とは周期的な運動をするものが一周期の内のどのタイミングにいるかを示す量です。その単位はラジアンを用います。
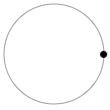
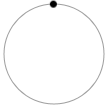左回りに等速円運動をする物体がちょうど真上にいるときの位相を 0 と定めると、
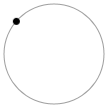左図のような位置にいるときの位相は \({\large\frac{π}{4}}\)
以下、次のようになります。
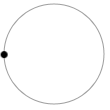
\({\large\frac{π}{2}}\)
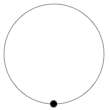
\(π\)
\({\large\frac{3}{2}}π\)
\(2π\) (=0 。\(2π\)で元に戻ります。)
単振動の場合においても、
たとえば真ん中にいるときの位相を 0 と定めると、
左図のような位置にいるときの位相は \({\large\frac{π}{4}}\)
以下、次のようになります。
\({\large\frac{π}{2}}\)
\(π\)
\({\large\frac{3}{2}}π\)
\(2π\) (=0)
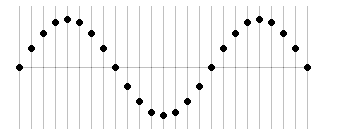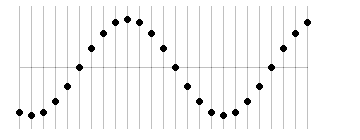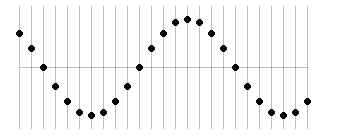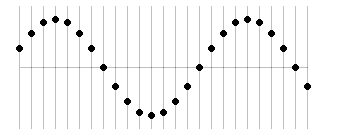正弦波の場合においても、
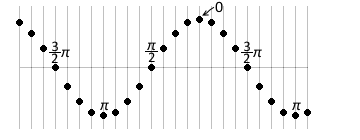
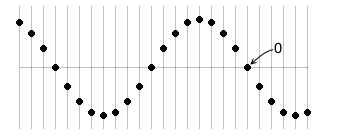左図のような点の位相を 0 と定めると、
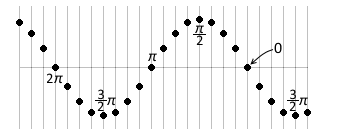各点の位相は左図のようになります。
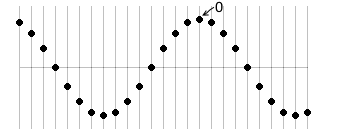もし、左図のような点の位相を 0 と定めれば、
各点の位相は左図のようになります。
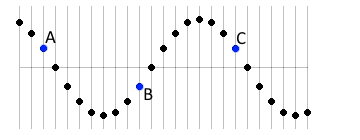A点とC点は同位相です。
A点とB点は位相が \(π\) だけズレています。
位相が \(π\) ズレた状態を逆位相ということがあります。また、位相が \(π\) ズレることを位相が逆転する、位相が反転する、などということがあります。
\(y = A\sin2π\big({\large\frac{t}{T}} - {\large\frac{x}{λ}}\big)\)
でいえば、\(\sin\) の中の \(2π\big({\large\frac{t}{T}} - {\large\frac{x}{λ}}\big)\) の部分が位相です。