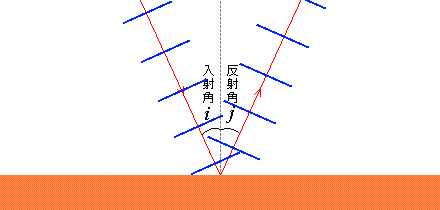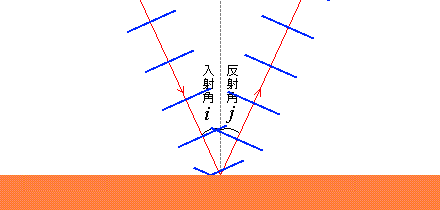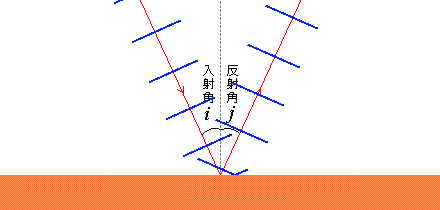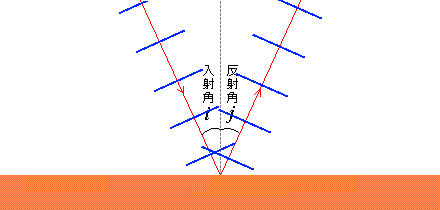波が境界面にぶつかるとき、波の進行方向と境界面の法線とのなす角を入射角といいます。量記号は \(i\) を使うことが多いです。incidence の \(i\) です。
「\(i\) は in だから入射」と覚えてください
同様に、反射した波の進行方向と境界面の法線とのなす角を反射角といいます。量記号は本項では \(j\) を使います。\(i\) の次の \(j\) です。reflection の \(r\) を使いたいところですがそうすると次項の refraction と被ってしまいます。
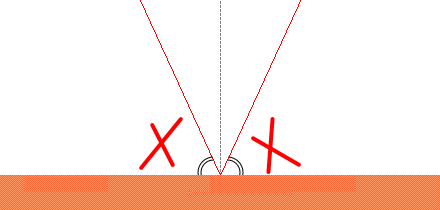これらの角は境界面とのなす角を定義してもいいのかもしれませんが、物理では慣習的に法線とのなす角を入射角・反射角と呼ぶことになってます。慣れないうちは間違いやすいです。
波が境界面に当って反射する場合、入射角と反射角は必ず等しくなります。反射の法則といいます。
ボールを壁に当てる場合は、入射角と反射角が等しくなるとは限りません。弾性衝突するかどうかわかりませんし、ボールが回転しているかもしれませんし、ボールと壁との間に摩擦があるかもしれません。
このような物体の衝突と違って波の場合は、必ず入射角と反射角が等しくなります。逆にいいますと、波の場合は反射角の角度を変えることはできない、ということです。
波において入射角と反射角が等しくなるのは、直感的に当たり前のことに感じますが、理由を説明するとすれば、均一な媒質においては波の進む速さが一定であり、ホイヘンスの原理がはたらくから、ということになります。
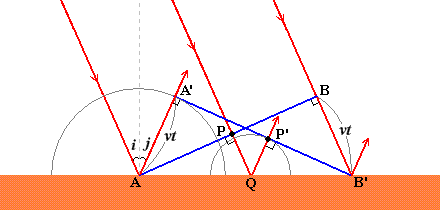
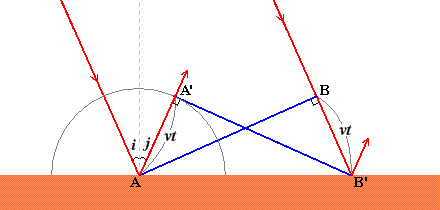左図においてABを入射波の波面とし、ある時刻に境界面に達したとします。波の速さを \(v\) [m/s] とし、Bが境界面に達するまでの時間を \(t\) [s] とすると、BB'の距離は \(vt\) [m] です。この \(t\) の時間の間にAから出た素元波の半径はこれも \(vt\) です。
この素元波の半円にB'から接線を引き、その接点をA'とすると、半径と接線は直角に交わるから∠AA'B'は直角、すなわち△AA'B'と△B'BAはどちらも直角三角形で、斜辺（AB'）と他の1辺（AA'=BB'=\(vt\)）が等しいので、合同となります。
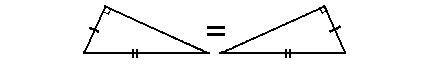三角形の合同条件というものを覚えているでしょうか。中学で習ったと思いますが、直角三角形の場合、斜辺（一番長い辺）と他の1辺が等しいとき、2つの三角形は合同（同一）であります。
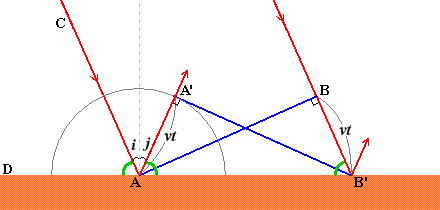左図の緑色の角に着目すると、
△AA'B'と△B'BAは合同であるので、∠A'AB'=∠BB'A。
また、C、Dを左図のように割り振ると、CAとBB'は平行であるから、∠CAD=∠BB'A。
よって、緑色の角はすべて同じで、∠CAD=∠A'AB'。
そして、
\(i\) = 90° - ∠CAD であり、
\(j\) = 90° - ∠A'AB' であるから、
\(i\) = \(j\)
このようにして入射角と反射角が等しいことが証明されます。
次に波面ABが反射すると本当に波面A'B'になるのかどうかを説明します。
波面AB上の任意の点Pが境界面上の点Qに達したとき、QからA'B'に下ろした垂線の足をP'とすると、PQとBB'は平行であるから、
\({\large\frac{\rm{PQ}}{\rm{BB'}}} = {\large\frac{\rm{AQ}}{\rm{AB'}}} = {\large\frac{\rm{AB'}-\rm{QB'}}{\rm{AB'}}}\)
\(= 1 - {\large\frac{\rm{QB'}}{\rm{AB'}}}\) \({\large(}\) QP'∥AA' であるので \({\large\frac{\rm{QB'}}{\rm{AB'}}} = {\large\frac{\rm{QP'}}{\rm{AA'}}}\) \({\large)}\)
\(= 1 - {\large\frac{\rm{QP'}}{\rm{AA'}}}\)
つまり、
\({\large\frac{\rm{PQ}}{\rm{BB'}}} = 1 - {\large\frac{\rm{QP'}}{\rm{AA'}}}\)
∴ \({\large\frac{\rm{PQ}}{\rm{BB'}}} + {\large\frac{\rm{QP'}}{\rm{AA'}}} = 1\)
AA' = BB' だから、
\({\large\frac{\rm{PQ}}{\rm{BB'}}} + {\large\frac{\rm{QP'}}{\rm{BB'}}} = 1\)
∴ PQ + QP' = BB' = \(vt\)
となります。
PQ + QP' = \(vt\) ということは、Pから出た素元波がQで跳ね返って接線にたどり着く距離が \(vt\) ということです。これはPから出た素元波は \(t\)秒後にちょうど接線にたどり着くということです。点PはAB上の任意の点であると定義しました。任意の点で成り立つということはあらゆる点で成り立つという意味です。つまり、AB上のあらゆる点は \(t\)秒後にA'B'上にたどり着くということです。すなわち、波面ABは \(t\)秒後に波面A'B'になる、といえます。