波の干渉

波の干渉

このような波と、

それを右にズラしたこのような波とを

2つ重ね合わせると、

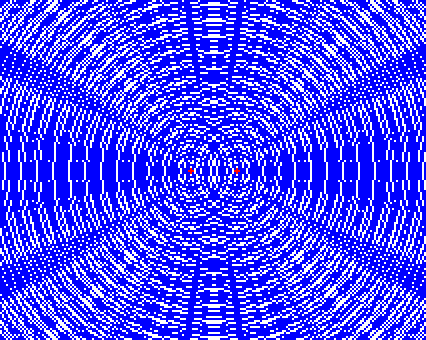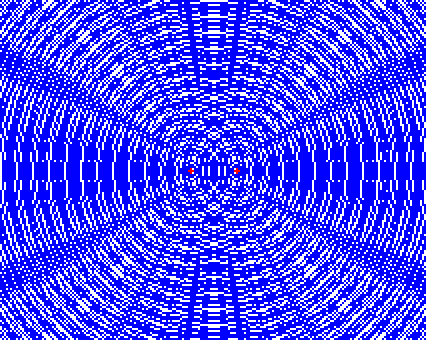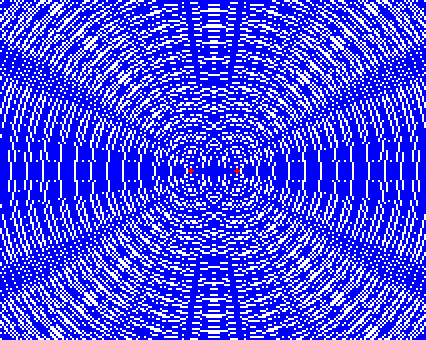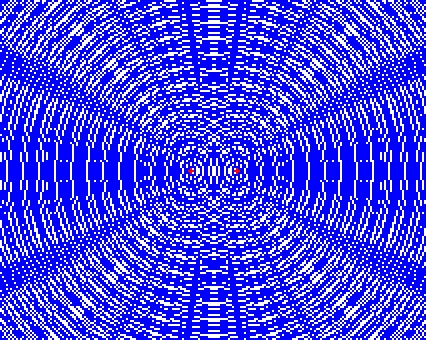このような波が現れます。

左図の緑で囲った部分は激しく振動します。2つの波源から出た波が重なって強め合ってる部分です。腹です。

赤で囲った部分はあまり振動しません。2つの波源から出た波が重なって弱め合ってる部分です。節です。

このように、複数の波が重なり合って強め合ったり弱め合ったりする現象を波の干渉といいます。

干渉の条件

どのような場所に腹ができて、どのような場所に節ができるのか考えてみます。

(1)図
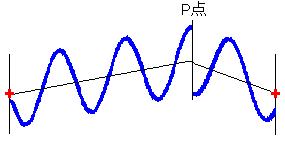2つの波源から出た波が左図のような点でぶつかった場合、波は弱め合います。逆位相の波同士は弱め合うのです。

(2)図
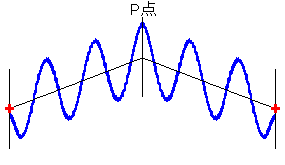しかし、左図のような点でぶつかれば強め合います。同位相の波同士は強め合うのです。

(3)図
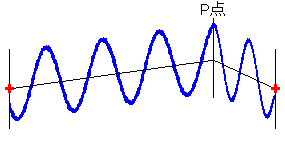左図のような点でぶつかっても強め合います。

(4)図
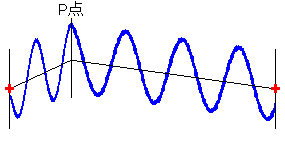また、左図のような点でも同じです。

(5)図
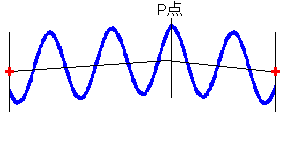このような点や、

(6)図
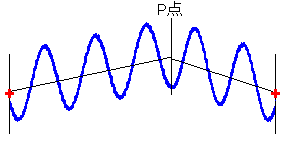このような点でも強め合います。この場合は -（マイナス）の方向に強め合ってます。これはたとえば水面をへこませているということです。

(3')図
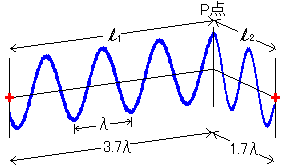左図のように符号を割り振り、l₁ と l₂ の差を求めると、

l₁ - l₂ = 3.7λ - 1.7λ = 2λ　…　(3)図の場合

l₁ - l₂ = 1.7λ - 3.7λ = -2λ　…　(4)図の場合

l₁ - l₂ = 2.7λ - 1.7λ = 1λ　…　(5)図の場合

l₁ - l₂ = 3.2λ - 2.2λ = 1λ　…　(6)図の場合

l₁ - l₂ = 2.7λ - 2.7λ = 0λ　…　(2)図の場合

l₁ - l₂ = 2.7λ - 1.2λ = 1.5λ　…　(1)図の弱め合う場合

このように考えてくると波が強め合う地点というのは l₁ と l₂ の差が λ の整数倍ということが分かります。

　　| l₁ - l₂ | = m λ　(m = 0,1,2,…)

これが強め合う地点、つまり腹のできる場所の条件となります。上で示した図の緑で囲った部分です。

次に弱め合う地点、つまり節のできる場所の条件を考えます。まず1つは (1)図で示した点です。

(7)図
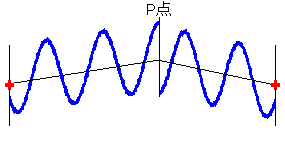その他、左図のような点 ( l₁ - l₂ = 2.7λ - 2.2λ = 0.5λ ) や、

(8)図
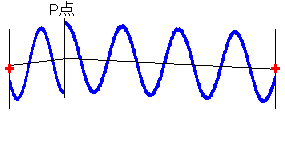左図のような点 ( l₁ - l₂ = 1.2λ - 3.7λ = -2.5λ ) です。

つまり波が弱め合う地点というのは l₁ と l₂ の差が、0.5λ、1.5λ、2.5λ、つまり λ の (m+\(\large{\frac{1}{2}}\))倍ということが分かります。

　　| l₁ - l₂ | = (m+\(\large{\frac{1}{2}}\)) λ　(m = 0,1,2,…)

これが弱め合う地点、つまり節のできる場所の条件となります。上で示した図の赤で囲った部分です。

まとめます。

双曲線

(1)図から(8)図で示した点をプロットすると左図のようになります。濃い青線が波の山で、薄い水色が波の谷を表しています。強め合う地点は青線と青線（または水色線と水色線）の交点になっており、弱め合う地点は青線と水色線の交点となってます。

強め合う地点を緑、弱め合う地点を赤で全てプロットしますと、左図のような双曲線が現れます。

双曲線を表す数式については数学で学ぶと思いますが、上で示した干渉条件の式は双曲線を形成する式になっています。

| l₁ - l₂ | = m λ　という式によって緑の点のラインが形成され、

| l₁ - l₂ | = (m+\(\large{\frac{1}{2}}\)) λ　という式によって赤の点のラインが形成されます。

そして左図の場合、m の値は 0 か 1 か 2 の３通りだけです。真ん中の縦の列が m=0 のラインで、脇に行くほど数値が大きくなります。2つの波源がもっと離れているか、もっと波長が小さければ m も 4、5、6、という値を取ります。双曲線の本数が増えるということです。

逆位相の2つの波源

ここまでの話は2つの波源が同じタイミング（同位相）の波を発生させた場合の話でしたが、

2つの波源が逆のタイミング（逆位相）の波を発生させた場合は、上の図において片方の発生源から出る波の青線と水色線が入れ替わるので、強め合う地点と弱め合う地点の条件が逆になります。

逆位相の2つの波源から出た波の干渉条件

強め合う条件　　| l₁ - l₂ | = (m+\(\large{\frac{1}{2}}\)) λ

弱め合う条件　　| l₁ - l₂ | = m λ

　　　　　　　　(m = 0,1,2,…)