(問4)
ア
時間 = \(\frac{距離}{速さ}\) だから、
T = \(\large{\frac{2L}{c}}\)
イ
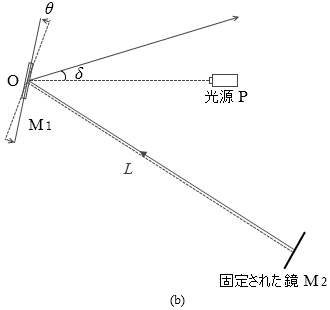
δ はデルタと読みます。ギリシャ文字の小文字です。『平面鏡の回転』で説明したように δ の角度は θ の2倍になります。
δ = 2θ
(問5)
この実験は「フーコーの光速度測定」という有名な実験です。
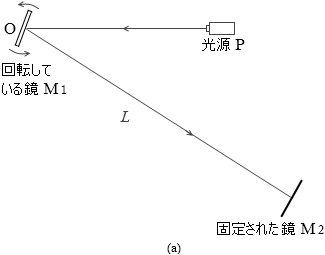
光の速度はとてつもなく速いので、普通なら、光源Pから出た光は鏡M1で反射して鏡M2に向かい、鏡M2で反射して元来た道をたどってスタート地点の光源Pに戻ります。しかし、鏡M1を超高速で回転させることにより、戻って来た光を δ だけズラすことができます。この δ と回転数を測定することによって光速 c を割り出すことができます。
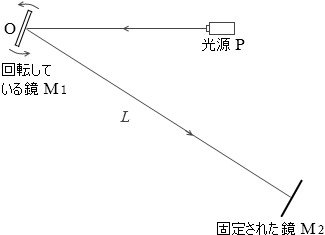 鏡M1は回転しているので色々な方向を向きますが、光源Pと鏡M2の中間の方向を向いた瞬間だけ、光線が往復運動して戻ってきます。
鏡M1は回転しているので色々な方向を向きますが、光源Pと鏡M2の中間の方向を向いた瞬間だけ、光線が往復運動して戻ってきます。
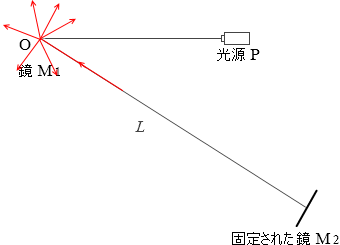 戻ってきた光線は様々な方向に反射されますが、
戻ってきた光線は様々な方向に反射されますが、
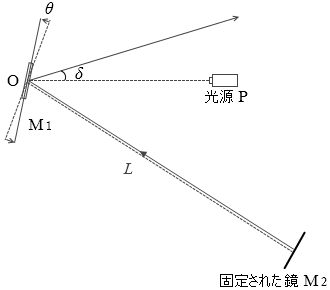 鏡M1がある回転数になると、δ の方角だけに反射されるようになります。
鏡M1がある回転数になると、δ の方角だけに反射されるようになります。
 何百回も回転して、毎回同じ方向に反射されるとなると測定誤差はあまり無いことになります。
何百回も回転して、毎回同じ方向に反射されるとなると測定誤差はあまり無いことになります。
鏡M1の1秒あたりの回転数を N [Hz] と置きますと、1回転あたりの秒数は
\(\large{\frac{1}{N}}\) [s]
であり、
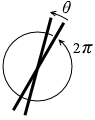 θ [rad] だけ回転する秒数は、(一周が 2π [rad] だから)
θ [rad] だけ回転する秒数は、(一周が 2π [rad] だから)
\(\large{\frac{1}{N}}\) × \(\large{\frac{θ}{2π}}\) [s]
です。
この秒数は、光がM1とM2を往復する時間でもあります。
δ = 2θ を代入しますと、
\(\large{\frac{1}{N}}\) × \(\large{\frac{δ}{4π}}\) [s]
であり、これが問4で求めた T = \(\large{\frac{2L}{c}}\) と等しいのだから、
\(\large{\frac{1}{N}}\) × \(\large{\frac{δ}{4π}}\) = \(\large{\frac{2L}{c}}\)
∴ c = \(\large{\frac{8πNL}{δ}}\) ……➊
と関係式が導かれ、N と L と δ を測定することによって光速 c が導き出せます。
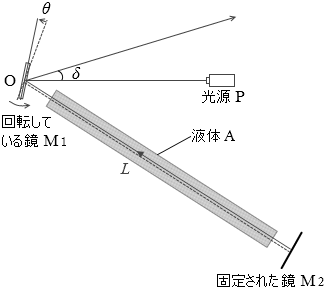
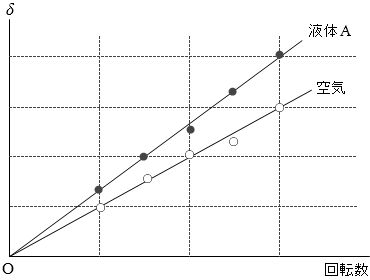
ここまでが「フーコーの光速度測定」の原理の話なのですが、本問は「液体A中の光速は、空気中の光速の何倍か」を聞いています。
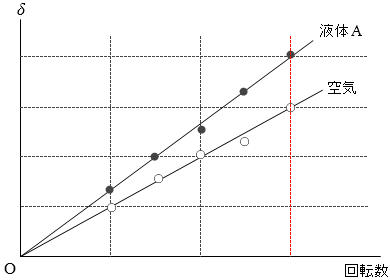 左図の赤線のラインに着目しますと、同じ回転数のときに液体Aは空気に比べ δ が \(\large{\frac{4}{3}}\)倍になっています。
左図の赤線のラインに着目しますと、同じ回転数のときに液体Aは空気に比べ δ が \(\large{\frac{4}{3}}\)倍になっています。
➊式により、光速 c と δ は反比例の関係にありますので、液体A中の光速は、空気中の光速の \(\large{\frac{3}{4}}\)倍と分かります。
答え ③ 0.75
 鏡M1は回転しているので色々な方向を向きますが、光源Pと鏡M2の中間の方向を向いた瞬間だけ、光線が往復運動して戻ってきます。
鏡M1は回転しているので色々な方向を向きますが、光源Pと鏡M2の中間の方向を向いた瞬間だけ、光線が往復運動して戻ってきます。 戻ってきた光線は様々な方向に反射されますが、
戻ってきた光線は様々な方向に反射されますが、 鏡M1がある回転数になると、δ の方角だけに反射されるようになります。
鏡M1がある回転数になると、δ の方角だけに反射されるようになります。 何百回も回転して、毎回同じ方向に反射されるとなると測定誤差はあまり無いことになります。
何百回も回転して、毎回同じ方向に反射されるとなると測定誤差はあまり無いことになります。 θ [rad] だけ回転する秒数は、(一周が 2π [rad]
θ [rad] だけ回転する秒数は、(一周が 2π [rad]  左図の赤線のラインに着目しますと、同じ回転数のときに液体Aは空気に比べ δ が \(\large{\frac{4}{3}}\)倍になっています。
左図の赤線のラインに着目しますと、同じ回転数のときに液体Aは空気に比べ δ が \(\large{\frac{4}{3}}\)倍になっています。