原子核の発見と原子の構造の解明に関する次の問い(問1~3)に答えよ。
(問1)金箔に照射した\(α\)粒子(電気量\(+2e\)、\(e\)は電気素量)の散乱実験の結果から、ラザフォードは、質量と正電荷が狭い部分に集中した原子核の存在を突き止めた。金の原子核による\(α\)粒子の散乱の様子を示した図として最も適当なものを、次の①~⑥のうちから一つ選べ。ただし、図中の黒丸は原子核の位置を、実線は原子核の周辺での\(α\)粒子の飛跡を模式的に示している。
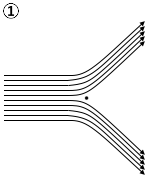
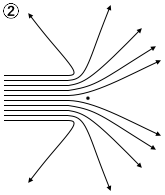
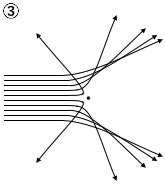
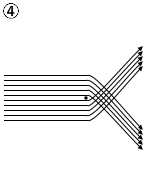
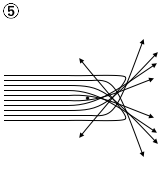
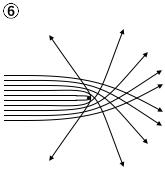
(問2)次の文章中の空欄ア・イに入れる語の組合せとして最も適当なものを、下の①~⑥のうちから一つ選べ。
電子が原子核のまわりを円運動していると考えるラザフォードの原子模型では、電子が電磁波を放射して徐々にアを失い、電子の軌道半径が時間とともに小さくなってしまうという問題があった。ボーアはこの問題を解決するために「原子中の電子は、ある条件を満足する円軌道上のみで運動している」という仮説を導入した。このとき、電子はある決まったエネルギーをもち電磁波を放射しない。この状態を定常状態という。
さらに、「電子がある定常状態から別のエネルギーをもつ定常状態に移るとき、その差のエネルギーをもつ1個のイが放出または吸収される」という仮説も導入し、水素原子のスペクトルの説明に成功した。
| ア | イ | |
|---|---|---|
| ① | 質量 | 光電子 |
| ② | 質量 | 光子 |
| ③ | エネルギー | 光電子 |
| ④ | エネルギー | 光子 |
| ⑤ | 電荷 | 光電子 |
| ⑥ | 電荷 | 光子 |
(問3)定常状態は、ド・ブロイによって提唱された物質波の考えを用いることにより、波動としての電子が原子核を中心とする円軌道上にあたかも定常波をつくっている状態だと解釈されるようになった。このとき、量子数 \(n\)(\(n\)=1,2,3,…)の定常状態における円軌道の半径 \(r\)、電子の質量 \(m\)、電子の速さ \(v\)、プランク定数 \(h\) の間に成り立つ関係式として正しいものを、次の①~⑥のうちから一つ選べ。
① \(πr^2 = \large\frac{nmv}{h}\)
#センター15本試物理