原子の構造
考えられた様々な原子模型
原子の構成要素の1つである電子が発見されてもしばらくの間は原子の構造がどういうものであるか解明できませんでした。原子は電気的に中性であり もちろんイオン化してない通常の原子のことです 、電子は負であることは分かっていました。となると原子は電子以外に正の電荷の何かによって構成されているということになります。
 J. J. トムソン
1856年–1940年のイギリスの物理学者、ジョゼフ・ジョン・トムソン。
J. J. トムソン
1856年–1940年のイギリスの物理学者、ジョゼフ・ジョン・トムソン。
『トムソンの実験』のトムソンです。
は正の電荷を持つ(パンのような)ものが原子全体を占めていて、
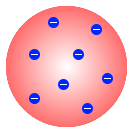 その中に負の電荷を持つ電子が(ブドウのように)埋まっていると考えました。ブドウパンモデルといいます
英語では plum pudding model というそうです
。
その中に負の電荷を持つ電子が(ブドウのように)埋まっていると考えました。ブドウパンモデルといいます
英語では plum pudding model というそうです
。
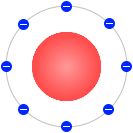 長岡半太郎
1865年–1950年の物理学者。
は中心部に正電荷の部分があり、その周りを電子が回っているという土星型モデルを提唱しました。
長岡半太郎
1865年–1950年の物理学者。
は中心部に正電荷の部分があり、その周りを電子が回っているという土星型モデルを提唱しました。
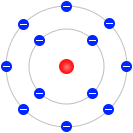 ラザフォード
1871年–1937年のニュージーランドの物理学者、アーネスト・ラザフォード。
は正電荷の中心部は非常に小さく、その周りのいくつかの軌道を電子が回っているというモデルを提唱しました。ラザフォードの原子模型といいます。
ラザフォード
1871年–1937年のニュージーランドの物理学者、アーネスト・ラザフォード。
は正電荷の中心部は非常に小さく、その周りのいくつかの軌道を電子が回っているというモデルを提唱しました。ラザフォードの原子模型といいます。
中心部が非常に小さいことは薄い金箔にα線(=ヘリウムの原子核であるα粒子の流れ)を当てる実験により解明されました。
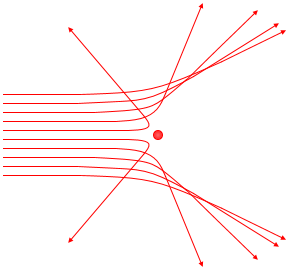 α粒子は電子の約7300倍の質量を持つので電子に当たったとしても直進します。しかし一部は進行方向がわずかに曲げられ、さらにそのごく一部(全体として8000個に1個くらい)は90°以上曲げられ(跳ね返され)ます(中心部もα粒子も正電荷であり互いに反発します、近いほど強く反発します)。このときの曲がり具合から金原子の中心部は 10-15~10-14m くらいの大きさであることが分かりました。原子の直径が 10-10m くらいなので、その10万分の1から1万分の1くらいの大きさです。
α粒子は電子の約7300倍の質量を持つので電子に当たったとしても直進します。しかし一部は進行方向がわずかに曲げられ、さらにそのごく一部(全体として8000個に1個くらい)は90°以上曲げられ(跳ね返され)ます(中心部もα粒子も正電荷であり互いに反発します、近いほど強く反発します)。このときの曲がり具合から金原子の中心部は 10-15~10-14m くらいの大きさであることが分かりました。原子の直径が 10-10m くらいなので、その10万分の1から1万分の1くらいの大きさです。
この中心部は原子核と名付けられました。
原子核は正の電荷を持ち、電子は負の電荷を持ち、それらがつり合って全体として原子は中性となっています。電子の電荷は - \(e\) [C] ですから、
電子が1個だけ含まれる原子
水素原子のことです。
の原子核の電荷は +\(e\) [C] であり、
電子が2個含まれる原子
ヘリウム原子のことです。
の原子核の電荷は +2\(e\) [C] であり、
電子が3個含まれる原子
リチウム原子のことです。
の原子核の電荷は +3\(e\) [C] です。
この電子の個数(=陽子の個数)によって原子番号というものが割り振られ、量記号としては \(Z\) が用いられることになりました。原子番号 \(Z\) の原子は、中心部に +\(Ze\) [C] の原子核を持ち、その周りを - \(e\) [C] の電子が\(Z\)個まわっています。
…と、ここまで詳細に原子の姿が明らかになったのですが、これではまだ不十分でした。
原子は特定の振動数の電磁波しか放出しないのですが、そのことが説明できませんでした。
水素原子のスペクトル
 原子が放つ光(電磁波)はその種類によって波長、あるいは振動数が決まっています。たとえば気体の水素を真空管の中に入れて放電させると左図のようなスペクトルが得られます。
原子が放つ光(電磁波)はその種類によって波長、あるいは振動数が決まっています。たとえば気体の水素を真空管の中に入れて放電させると左図のようなスペクトルが得られます。
左から順番に 656.28nm、486.13nm、434.05nm、410.17nm nm(ナノメートル) = 10-9 m の線スペクトルなのですが、この水素のスペクトルの波長についてバルマー 1825年–1898年のスイスの物理学者、ヨハン・ヤコブ・バルマー。 は
\(λ\) = 3.6456×10-7 × \(\Big({\large\frac{n^2}{n^2-2^2}}\Big)\) ……①
という式を満たすことを発見しました。
\(n\) = 3,4,5,6 を代入するとそれぞれの値になります(ほんの少しズレますが)。
(\(n\) = 3)
\(λ_3\) = 3.6456×10-7 × \(\Big({\large\frac{9}{9-4}}\Big)\) = 3.6456×10-7 × 1.8 = 6.56208×10-7 = 656.208×10-9
(\(n\) = 4)
\(λ_4\) = 3.6456×10-7 × \(\Big({\large\frac{16}{16-4}}\Big)\) ≒ 3.6456×10-7 × 1.333333 ≒ 4.8608×10-7 = 486.08×10-9
(\(n\) = 5)
\(λ_5\) = 3.6456×10-7 × \(\Big({\large\frac{25}{25-4}}\Big)\) ≒ 3.6456×10-7 × 1.190476 ≒ 4.34×10-7 = 434×10-9
(\(n\) = 6)
\(λ_6\) = 3.6456×10-7 × \(\Big({\large\frac{36}{36-4}}\Big)\) = 3.6456×10-7 × 1.125 = 4.1013×10-7 = 410.13×10-9
下でも同じような計算をしてます。
それにしてもどうやってこの式に気づいたか不思議です。バルマーは物理学者であると同時に数学者でもあったようです。
さらにリュードベリ 1854年–1919年のスウェーデンの物理学者、ヨハネス・リュードベリ。 はこの式の両辺の分母分子を入れ替え、
\({\large\frac{1}{λ}}\) = \({\large\frac{1}{3.6456×10^{-7}}}\) × \(\Big({\large\frac{n^2-2^2}{n^2}}\Big)\)
= \({\large\frac{1}{3.6456×10^{-7}}}\) × \(\Big(1-{\large\frac{2^2}{n^2}}\Big)\)
= \({\large\frac{1}{3.6456×10^{-7}}}\) × \(\Big({\large\frac{2^2}{2^2}}-{\large\frac{2^2}{n^2}}\Big)\)
= \({\large\frac{1}{3.6456×10^{-7}}}\) × 22 × \(\Big({\large\frac{1}{2^2}}-{\large\frac{1}{n^2}}\Big)\)
≒ 1.097×107 × \(\Big({\large\frac{1}{2^2}}-{\large\frac{1}{n^2}}\Big)\)
この式の 22 の部分を \(n'^{\ 2}\) としたときに \(n\) の部分が \(n'\)+1 以上の整数となり、上で示した4つ以外に実験で発見されたスペクトルがこの式を満たすことを発見しました。
\({\large\frac{1}{λ}}\) というのは波長の逆数ですから1mあたり波がいくつあるかを表す量です。波数と呼ばれます。単位は [/m] です。振動数と似ていて紛らわしいです。
\({\large\frac{1}{λ}}\) は \(\tilde{ν}\)(ニューチルダ)で表すこともあります。
これは \(ν\) とは違います。
\({\large\frac{1}{λ}}\) = \(\tilde{ν}\) で \(c\) = \(νλ\) なので
\(\tilde{ν}\) = \({\large\frac{ν}{c}}\) です。
1.097×107 はリュードベリ定数といいます。これも単位は [/m] です。 \(R\) で表します。
水素原子のスペクトル(リュードベリの式)
\(\boldsymbol{{\large\frac{1}{λ}}}\) = \(\boldsymbol{R\Big({\large\frac{1}{n'^2}}-{\large\frac{1}{n^2}}\Big)}\)
\((n' = 1,2,3,…)\)
\((n = n'+1,n'+2,n'+3,…)\)
この式において
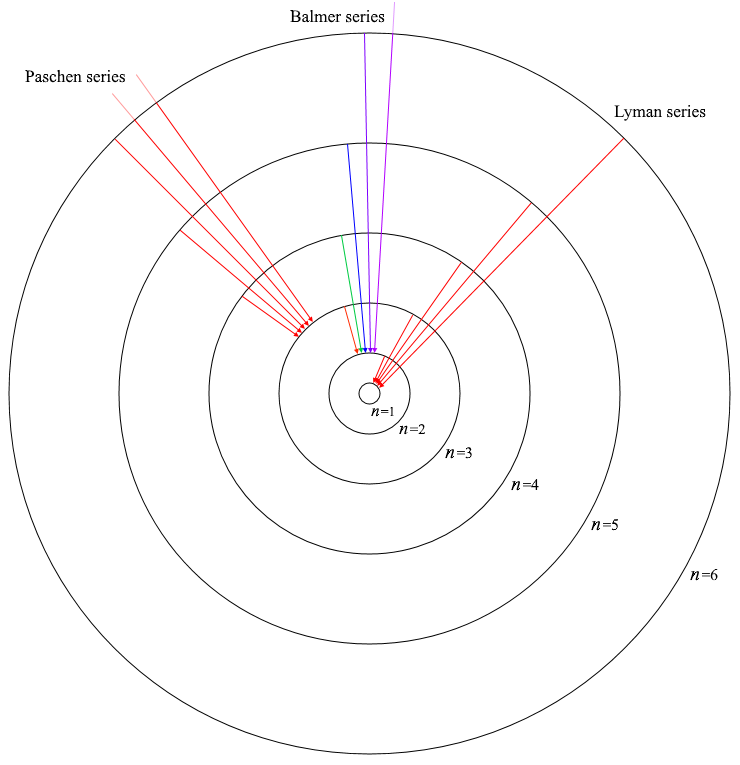
\(n'\) = 1 の場合のスペクトルグループをライマン系列
1874年–1954年のアメリカの物理学者、セオドア・ライマンが発見しました。
といいます。紫外線の領域のスペクトルです。
\({\large\frac{1}{λ}}\) = \(R\Big({\large\frac{1}{1^2}}-{\large\frac{1}{n^2}}\Big)\) \((n = 2,3,4,…)\)
\(n'\) = 2 の場合のスペクトルグループをバルマー系列といいます。可視光線の領域のスペクトルです。上の①式のことです。
\({\large\frac{1}{λ}}\) = \(R\Big({\large\frac{1}{2^2}}-{\large\frac{1}{n^2}}\Big)\) \((n = 3,4,5,…)\)
\(n'\) = 3 の場合のスペクトルグループをパッシェン系列 1865年–1947年のドイツの物理学者、フリードリッヒ・パッシェンが発見しました。 といいます。赤外線の領域のスペクトルです。
\({\large\frac{1}{λ}}\) = \(R\Big({\large\frac{1}{3^2}}-{\large\frac{1}{n^2}}\Big)\) \((n = 4,5,6,…)\)
(\(n'\) ≧ 4 の場合にもそれぞれ名前が付いていますが省略します)

ボーアの量子条件と振動数条件
電荷というものは加速度運動をするとき、電磁波を放出します。(残念ながらこれは大学で学びます)
そうしますと円運動する電子は電磁波を放出するということになります。円運動は等速で回っていたとしても加速度運動です。中心方向に向心力がはたらいています。加速しています。
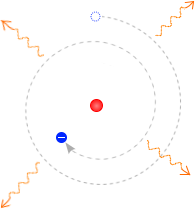 電磁波を放出するということはエネルギーを失うということです
円錐振り子などはエネルギーを失うことはありません。失うとしたらその原因は空気抵抗です。電磁波を放出してエネルギーを失うということはありません。
電磁波を放出するということはエネルギーを失うということです
円錐振り子などはエネルギーを失うことはありません。失うとしたらその原因は空気抵抗です。電磁波を放出してエネルギーを失うということはありません。
電荷は円運動という加速度運動をすると電磁波を放出してエネルギーを失います。
。エネルギーを失うということは軌道半径が小さくなるということです。電子が原子核とくっついてしまうということです。また、エネルギーの減少は連続的に徐々に起こるはずであり、飛び飛びの値の電磁波を放出するという実験結果と矛盾します。
ボーア 1885年–1962年のデンマークの物理学者、ニールス・ボーア。 はこれらの矛盾を解決するために以下のような2つの仮説を提唱しました。
仮説1:電子は定常波ができるような軌道を回っている
1つ目は、電子というのは粒子であると同時に波動であり、その(電子波の)波長は \(λ\) = \({\large\frac{h}{mv}}\) であるが、電子の円軌道の円周の長さがこの波長の自然数倍となるとき、定常波ができて安定し、電磁波を放出せず、永続的な円運動をする、というものです このときなぜ電磁波を放出しないかについては大学で学びます。 。ボーアの量子条件といいます。また、安定した状態を定常状態といい、このときの自然数を量子数(\(n\)で表す)といいます。
6\(λ\)
円周が波長の自然数倍の状態
6.5\(λ\)
円周が波長の自然数倍ではない状態
円軌道の半径を \(r\) としますと円周は \(2πr\) ですから、
\(2πr\) = \(nλ\) = \(n{\large\frac{h}{mv}}\)
となるわけですが、この式の左辺と右辺を取り出して変形しますと、
\(mvr\) = \(n{\large\frac{h}{2π}}\)
となり、主にこの式のことをボーアの量子条件と呼びます。\(h\) はプランク定数、\(m\) は電子の質量、\(v\) は電子の速さです。
ボーアの量子条件
\(\boldsymbol{mvr}\) = \(\boldsymbol{n{\large\frac{h}{2π}}}\) \((n = 1,2,3,…)\)
\(n\) =1
\(n\) =2
\(n\) =3
\(n\) =4
\(n\) =5
ちょっと誤解しやすいのは、これは電子が波打ちながら周回しているわけではないということです。
このような感じではなく、
このような感じです。
玉が波打ちながら周回しているというよりは波のようなものが周回しているという感じです。
あと、(下で説明しますが)軌道半径は \(n^2\) に比例しますので実際の大きさの差は以下のようになります。
仮説2:エネルギー準位の差が光子のエネルギー
2つ目の仮説は、電子が量子数 \(n\) の定常状態の軌道から量子数 \(n'\ (n'<n)\) の定常状態の軌道に移るとき、1個の光子を放出(逆に \(n'\) から \(n\) に移るときは吸収)するが、その光子のエネルギーは量子数 \(n\) の定常状態のエネルギーと量子数 \(n'\) の定常状態のエネルギーとの差になっている、というものです。ボーアの振動数条件といいます。光子のエネルギーというのは実質的に光子の振動数のことなので”振動数”条件です。
電子が定常状態の軌道を回っているときのエネルギーをエネルギー準位 「準位」は、土地の高低などを表す水準という言葉になぞらえて作られた物理用語のようです。 といいますが、これを \(E_n\) 、\(E_{n'}\) と表すことにすると、
\(E_n - E_{n'}\) = \(hν\)
となります。1個の光子のエネルギーは \(hν\) [J] です。
ボーアの振動数条件
\(\boldsymbol{E_n - E_{n'}}\) = \(\boldsymbol{hν}\)
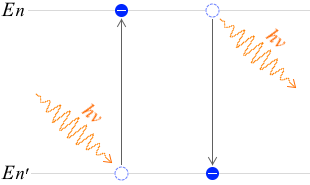 イメージはこんな感じです。
イメージはこんな感じです。
これは光電効果とは少し違います。電子が原子の外へ飛び出すというわけではありません。
高校物理では最も基本的な元素である水素原子のエネルギー準位についてしか学びませんが、ボーアの振動数条件は水素以外の原子についても成り立ちます。原子の種類によって放射、吸収される電磁波の振動数が決まっています。
水素原子の軌道半径とエネルギー準位
水素原子の軌道半径
水素原子は原子核の周りを1個の電子が回っている原子ですが、このときの電子の円軌道の半径を求めてみます。
原子核と電子との間には静電気力(クーロン力) \(F\) = \(k_0{\large\frac{e^2}{r^2}}\)
\(F\) = \(k_0{\large\frac{q_1q_2}{r^2}}\)
において
原子核の電荷:\(q_1\) → \(e\)
電子の電荷:\(q_2\) → \(e\)
比例定数として真空中の値:\(k\) → \(k_0\) を採用しています
がはたらいていて、これが向心力
\(F\) = \(m{\large\frac{v^2}{r}}\)
となって電子は原子核の周りを等速円運動をしていると考えられますので、
\(m{\large\frac{v^2}{r}}\) = \(k_0{\large\frac{e^2}{r^2}}\)
という式(等速円運動の運動方程式)が立てられます。この式を変形して、
\(mv^2\) = \(k_0{\large\frac{e^2}{r}}\) ……②
この式にボーアの量子条件 \(mvr\) = \(n{\large\frac{h}{2π}}\) を変形した式 \(v\) = \(n{\large\frac{h}{2πmr}}\) を代入して \(v\) を消去すると、
\(m(n{\large\frac{h}{2πmr}})^2\) = \(k_0{\large\frac{e^2}{r}}\)
∴ \(m{\large\frac{n^2h^2}{4π^2m^2r^2}}\) = \(k_0{\large\frac{e^2}{r}}\)
∴ \({\large\frac{n^2h^2}{4π^2mr^2}}\) = \(k_0{\large\frac{e^2}{r}}\)
∴ \({\large\frac{n^2h^2}{4π^2mr}}\) = \(k_0e^2\)
∴ \({\large\frac{n^2h^2}{4π^2k_0me^2}}\) = \(r\)
∴ \(r\) = \({\large\frac{h^2}{4π^2k_0me^2}}⋅n^2\)
水素原子の軌道半径
\(\boldsymbol{r}\) = \(\boldsymbol{{\large\frac{h^2}{4π^2k_0me^2}}⋅n^2}\) \((n = 1,2,3,…)\)
水素原子のエネルギー準位
次に水素原子の電子のエネルギーを求めてみます。
電子のエネルギーというのは電子の運動エネルギーと電子の位置エネルギーを足したものです。
電子の位置エネルギーというのは、電子と原子核との間にはたらく静電気力による位置エネルギーのことです。静電気力 電子が負で原子核が正ですのでこの静電気力は引力です。斥力ではありません。 による位置エネルギーは万有引力による位置エネルギーと同じように考えて求めます。
万有引力は
\(F\) = \(G{\large\frac{Mm}{r^2}}\)
で、その位置エネルギーは
\(U\) = \(-G{\large\frac{Mm}{r}}\)
です。
同じように考えて、電子と原子核との間にはたらく静電気力が
\(F\) = \(k_0{\large\frac{e^2}{r^2}}\)
であるのだから(上の『水素原子の軌道半径』参照)、電子の位置エネルギーは
\(U\) = \(-k_0{\large\frac{e^2}{r}}\)
です。
電子の運動エネルギーというのは \({\large\frac{1}{2}}mv^2\) ですが、②式 \(mv^2\) = \(k_0{\large\frac{e^2}{r}}\) より、 他に、ボーアの量子条件 \(mvr\) = \(n{\large\frac{h}{2π}}\) を代入する計算方法もあります。qOCC2 の(問3)で紹介しています。
\({\large\frac{1}{2}}mv^2\) = \({\large\frac{1}{2}}k_0{\large\frac{e^2}{r}}\)
です。
よって電子のエネルギー(\(E\) とする)は
\(E\) = 電子の位置エネルギー + 電子の運動エネルギー
= \(-k_0{\large\frac{e^2}{r}}+{\large\frac{1}{2}}k_0{\large\frac{e^2}{r}}\)
= \(-{\large\frac{k_0e^2}{2r}}\)
この式は定常状態のときだけでなく一般的な状態のエネルギーを表しているので、定常状態の場合である(すなわち量子数 \(n\) を含む式である)水素原子の軌道半径の式 \(r\) = \({\large\frac{h^2}{4π^2k_0me^2}}⋅n^2\) を代入します。
\(E\) = \(-{\large\frac{k_0e^2}{2}} × {\large\frac{1}{r}}\)
\(E_n\) = \(-{\large\frac{k_0e^2}{2}} × {\large\frac{4π^2k_0me^2}{h^2n^2}}\)
= \(-{\large\frac{2π^2{k_0}^2me^4}{h^2}}⋅{\large\frac{1}{n^2}}\)
水素原子のエネルギー準位
\(\boldsymbol{E_n}\) = \(\boldsymbol{-{\large\frac{2π^2{k_0}^2me^4}{h^2}}⋅{\large\frac{1}{n^2}}}\) \((n = 1,2,3,…)\)
単位は [J] です。[eV] で表したい場合は \(e\) で割ればいいので \(e^4\) の部分が \(e^3\) となります。(以下を参照)
基底状態と励起状態
上式の \(n\) 以外の量は定数で、具体的には以下のような値です。 各量とも5桁の細かい値を使って計算することにします。3桁くらいの値だと教科書に載っている \(E_n\) の値とはズレてしまいます。
\(k_0\) = 8.9876×109 [N⋅m2/C2] :クーロンの法則の比例定数
\(m\) = 9.1094×10-31 [kg] :電子の質量
\(e\) = 1.6022×10-19 [C] :電気素量
\(h\) = 6.6261×10-34 [J⋅s] :プランク定数
これらを代入してみます。
\(E_n\) = \(-{\large\frac{2π^2{k_0}^2me^4}{h^2}}⋅{\large\frac{1}{n^2}}\)
= \(-{\large\frac{2⋅(3.1416)^2⋅(8.9876×10^9)^2⋅(9.1094×10^{-31})⋅(1.6022×10^{-19})^4}{(6.6261×10^{-34})^2}}⋅{\large\frac{1}{n^2}}\) \({\rm{\large\frac{[N⋅m^2/C^2]^2⋅[kg]⋅[C]^4}{[J⋅s]^2}}}\)
= \(-{\large\frac{2⋅(3.1416)^2⋅(8.9876)^2⋅(9.1094)⋅(1.6022)^4}{(6.6261)^2}}\)⋅\(\large{\frac{(10^9)^2⋅(10^{-31})⋅(10^{-19})^4}{(10^{-34})^2}}⋅{\large\frac{1}{n^2}}\)
= \(-{\large\frac{2⋅(9.86965056)⋅(80.77695376)⋅(9.1094)⋅(6.5897192105706256)}{(43.90520121)}}⋅{\large\frac{(10^{18})⋅(10^{-31})⋅(10^{-76})}{(10^{-68})}}⋅{\large\frac{1}{n^2}}\)
≒ - (2180.0173689950447041189465117043)⋅(10-21)⋅\({\large\frac{1}{n^2}}\)
≒ - (2.1800×10-18)⋅\({\large\frac{1}{n^2}}\) \({\rm{\large\frac{[N⋅m^2/C^2]^2⋅[kg]⋅[C]^4}{[J⋅s]^2}}}\)
= - (2.1800×10-18)⋅\({\large\frac{1}{n^2}}\) \({\rm{\large\frac{[N^2⋅m^4]⋅[kg]}{[J^2⋅s^2]}}}\)
= - (2.1800×10-18)⋅\({\large\frac{1}{n^2}}\) \({\rm{\large\frac{[N^2⋅m^2]⋅[m]⋅[m/s^2]⋅[kg]}{[J^2]}}}\)
= - (2.1800×10-18)⋅\({\large\frac{1}{n^2}}\) \({\rm{\large\frac{[J^2]⋅[m]⋅[N]}{[J^2]}}}\)
単位の演算です。
[N] × [m] = [J]
∵(力)×(距離)=(仕事)
[m/s2] × [kg] = [N]
∵(加速度)×(質量)=(力)
= - (2.1800×10-18)⋅\({\large\frac{1}{n^2}}\) \({\rm{\large\frac{[J^2]⋅[J]}{[J^2]}}}\)
= - (2.1800×10-18)⋅\({\large\frac{1}{n^2}}\) [J]
\(e\) = 1.6022×10-19 で割って単位を [J] から [eV] に変換すると、
\(E_n\) = \(-{\large\frac{2.1800×10^{-18}}{1.6022×10^{-19}}}⋅{\large\frac{1}{n^2}}\) [eV]
≒ \(-{\large\frac{1.3606}{10^{-1}}}⋅{\large\frac{1}{n^2}}\) [eV]
≒ -13.6 × \({\large\frac{1}{n^2}}\) [eV]
この式の \(n\) は上で説明したように量子数と呼ばれるものですが、特に \(n\) = 1 のときの状態を基底状態といい、それ以外の \(n\) ≧ 2 のときの状態を励起状態といいます。それぞれの状態のときのエネルギー準位を求めてみます。
(\(n\) = 1)
\(E_1\) = -13.6 × \({\large\frac{1}{1^2}}\) = -13.6 [eV] 基底状態
(\(n\) = 2)
\(E_2\) = -13.6 × \({\large\frac{1}{2^2}}\) = -3.40 [eV] 励起状態
(\(n\) = 3)
\(E_3\) = -13.6 × \({\large\frac{1}{3^2}}\) = -1.51 [eV] 励起状態
(\(n\) = 4)
\(E_4\) = -13.6 × \({\large\frac{1}{4^2}}\) = -0.85 [eV] 励起状態
(\(n\) = 5)
\(E_5\) = -13.6 × \({\large\frac{1}{5^2}}\) = -0.54 [eV] 励起状態
(\(n\) = 6)
\(E_6\) = -13.6 × \({\large\frac{1}{6^2}}\) = -0.38 [eV] 励起状態
・
・
・
(\(n\) が大きくなるにつれて 0eV に近づいていきます)
改めて水素原子のスペクトル
改めて水素原子のスペクトルの式
\(E_n\) = \(-{\large\frac{2π^2{k_0}^2me^4}{h^2}}⋅{\large\frac{1}{n^2}}\)
をボーアの振動数条件の式
\(E_n - E_{n'}\) = \(hν\)
に代入しますと、
\(hν\) = \(E_n - E_{n'}\)
= \(-{\large\frac{2π^2{k_0}^2me^4}{h^2}}⋅{\large\frac{1}{n^2}} - \Big(-{\large\frac{2π^2{k_0}^2me^4}{h^2}}⋅{\large\frac{1}{n'^2}}\)\(\Big)\)
= \({\large\frac{2π^2{k_0}^2me^4}{h^2}}⋅{\large\frac{1}{n'^2}} - {\large\frac{2π^2{k_0}^2me^4}{h^2}}⋅{\large\frac{1}{n^2}}\)
= \({\large\frac{2π^2{k_0}^2me^4}{h^2}}\Big({\large\frac{1}{n'^2}}-{\large\frac{1}{n^2}}\Big)\)
さらに両辺を \(h\) で割りますと、
\(ν\) = \({\large\frac{2π^2{k_0}^2me^4}{h^3}}\Big({\large\frac{1}{n'^2}}-{\large\frac{1}{n^2}}\Big)\)
また、光速を \(c\) としますと \(c\) = \(νλ\) の関係がありますから \({\large\frac{1}{λ}}\) = \({\large\frac{ν}{c}}\) であり、これに上式を代入しますと、
\({\large\frac{1}{λ}}\) = \({\large\frac{2π^2{k_0}^2me^4}{ch^3}}\Big({\large\frac{1}{n'^2}}-{\large\frac{1}{n^2}}\Big)\)
となります。実はこれが上で示した水素原子のスペクトルの式(リュードベリの式)
\({\large\frac{1}{λ}}\) = \(R\Big({\large\frac{1}{n'^2}}-{\large\frac{1}{n^2}}\Big)\)
であり、\(R\) = \({\large\frac{2π^2{k_0}^2me^4}{ch^3}}\)
となります。\({\large\frac{2π^2{k_0}^2me^4}{h^2}}\) については上で計算して 2.1800×10-18 の値を得ていますが、これ以外の残りの \(c\) = 2.9979×108 [m/s] 、\(h\) = 6.6261×10-34 [J⋅s] を代入して計算をしてみますと、
\(R\) = \({\large\frac{2.1800×10^{-18}}{ch}}\)
\(R\) = \({\large\frac{2.1800×10^{-18}}{2.9979×10^{8}×6.6261×10^{-34}}}\) \({\rm{\large\frac{[J]}{[m/s]⋅[J⋅s]}}}\)
= \({\large\frac{2.1800}{2.9979×6.6261}}⋅{\large\frac{10^{-18}}{ 10^{8}×10^{-34}}}\) \({\rm{\large\frac{[J]}{[m]⋅[J]}}}\)
≒ 0.10974414657934852500713111675217×108 [/m]
≒ 1.097×107 [/m]
となり、上で示した値と一致します。
実際の波長を求めてスペクトルの図を描いてみる
水素原子のスペクトルの式
\({\large\frac{1}{λ}}\) = 1.097×107 × \(\Big({\large\frac{1}{n'^2}}-{\large\frac{1}{n^2}}\Big)\)
の \(n'\)、\(n\) の部分に量子数を代入して実際の波長を求めてみます。
\(n'\) = 1、\(n\) = 2 を代入しますと、
\({\large\frac{1}{λ}}\) = 1.097×107 × \(\Big({\large\frac{1}{1^2}}-{\large\frac{1}{2^2}}\Big)\)
= 1.097×107 × \(\Big({\large\frac{3}{4}}\Big)\)
∴ \(λ\) = \({\large\frac{4}{1.097×3}}\)×10-7
≒ 1.215×10-7 [m]
光速 \(c\) = 2.9979×108 [m/s] をこの値で割れば振動数 \(ν\) の値も導き出せます。
\(c\) = \(νλ\) の関係がありますので。
上で説明したようにこの式はボーアの振動数条件の式から導き出されたものであり、ボーアの振動数条件というのは電子が量子数 \(n\) の軌道から量子数 \(n'\) の軌道に移るときにそれに見合った光子を放出する(\(n'\) から \(n\) に移る場合は吸収する)ということです。
つまり、\(n'\) = 1、\(n\) = 2 を代入して \(λ\) = 1.215×10-7 [m] の値を得たということは、水素原子において電子が \(n\) = 2 の軌道から \(n\) = 1 の軌道に落ちると、1.215×10-7 [m] の光を放つということです。逆に、1.215×10-7 [m] の光を当てると電子が \(n\) = 1 の軌道から \(n\) = 2 の軌道に上がる、ということです。
他にも様々な値を代入して波長の大きさを計算しますと以下のようになります。
水素原子のスペクトルの式を以下のように変形すると計算が少し楽になります。
\({\large\frac{1}{λ}}\) = 1.097×107 × \(\Big({\large\frac{1}{n'^2}}-{\large\frac{1}{n^2}}\Big)\)
∴ \({\large\frac{1}{λ}}\) = 1.097×107 × \(\Big({\large\frac{n^2-n'^2}{n'^2n^2}}\Big)\)
∴ \(λ\) = \({\large\frac{n^2n'^2}{1.097×10^7×(n^2-n'^2)}}\)
(ライマン系列)
\(n'\) = 1、\(n\) = 2 → \(λ\) = 1.215×10-7 [m]
\(n'\) = 1、\(n\) = 3 → \(λ\) = 1.026×10-7 [m]
\(n'\) = 1、\(n\) = 4 → \(λ\) = 0.972×10-7 [m]
\(n'\) = 1、\(n\) = 5 → \(λ\) = 0.950×10-7 [m]
\(n'\) = 1、\(n\) = 6 → \(λ\) = 0.938×10-7 [m]
︙
(バルマー系列。以下の値は上でも示しました)
\(n'\) = 2、\(n\) = 3 → \(λ\) = 6.563×10-7 [m] ……③
\(n'\) = 2、\(n\) = 4 → \(λ\) = 4.862×10-7 [m]
\(n'\) = 2、\(n\) = 5 → \(λ\) = 4.341×10-7 [m]
\(n'\) = 2、\(n\) = 6 → \(λ\) = 4.102×10-7 [m]
\(n'\) = 2、\(n\) = 7 → \(λ\) = 3.970×10-7 [m]
︙
(パッシェン系列)
\(n'\) = 3、\(n\) = 4 → \(λ\) = 18.752×10-7 [m]
\(n'\) = 3、\(n\) = 5 → \(λ\) = 12.819×10-7 [m]
\(n'\) = 3、\(n\) = 6 → \(λ\) = 10.939×10-7 [m]
\(n'\) = 3、\(n\) = 7 → \(λ\) = 10.050×10-7 [m]
\(n'\) = 3、\(n\) = 8 → \(λ\) = 9.547×10-7 [m]
︙
(それぞれ \(n\) が大きくなるにつれて一定値に近づいていきます)
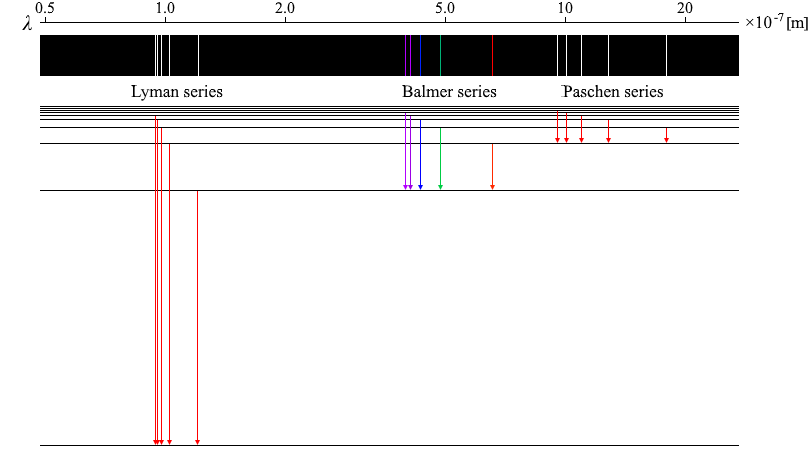
スペクトル図はこのようになります。

横軸は圧縮してあります。
スペクトルの順番は
㉕㉔㉓㉒㉑ ⑮⑭⑬⑫⑪ ⑤④③②①
というよりは
㉑㉒㉓㉔㉕ ⑪⑫⑬⑭⑮ ①②③④⑤
という感じになっています。
水素原子のエネルギー準位の図
エネルギー準位の図も描いてみます。
水平線を引いてその高さでエネルギー準位の大きさを表現します。各値は上で求めました。
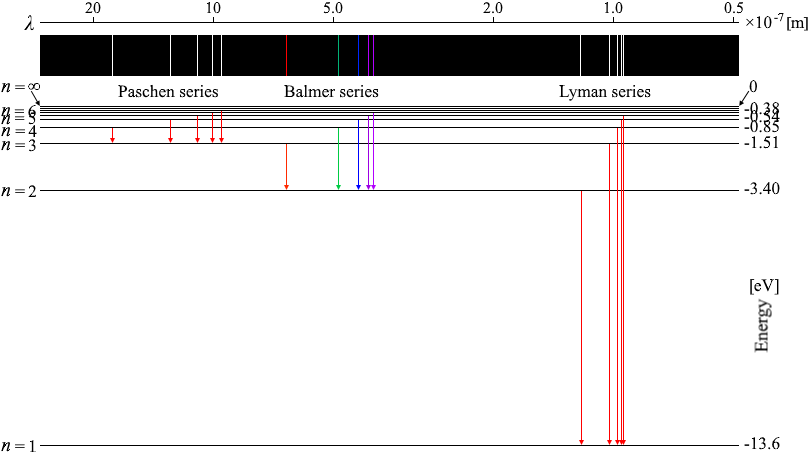
矢印は下向きの場合だけを描きましたが、上向きの場合もあります。電磁波(光子)を放出する場合が下向きで、電磁波(光子)を吸収する場合が上向きです。
矢印が長いほどエネルギーが大きいということであり、つまり振動数が大きい、波長が小さい、ということです。
上図は右に行くほど波長が小さくなるよう描きましたが、逆に左に行くほど小さくなるよう描く場合もあります。
水素原子の軌道半径の図
軌道半径の様子も描いてみます。
上のエネルギー準位は量子数 \(n\) が大きくなるほど間隔が狭くなっていきますが、軌道半径は逆です。軌道半径を表す式は上で示したように
\(r\) = \({\large\frac{h^2}{4π^2k_0me^2}}⋅n^2\)
であり、\({\large\frac{h^2}{4π^2k_0me^2}}\) 部分は計算すると 5.292×10-11 になるので、
上の『基底状態と励起状態』でやったのと同じような計算をします。
\(h\) = 6.6261×10-34 [J⋅s]
\(k_0\) = 8.9876×109 [N⋅m2/C2]
\(m\) = 9.1094×10-31 [kg]
\(e\) = 1.6022×10-19 [C]
を代入します。
\({\large\frac{h^2}{4π^2k_0me^2}}\)
= \({\large\frac{(6.6261×10^{-34})^2}{4⋅(3.1416)^2⋅8.9876×10^{9}⋅9.1094×10^{-31}⋅(1.6022×10^{-19})^2}}\) \({\rm{\large\frac{[J⋅s]^2}{[N⋅m^2/C^2]⋅[kg]⋅[C]^2}}}\)
= \({\large\frac{(6.6261)^2}{4⋅(3.1416)^2⋅8.9876⋅9.1094⋅(1.6022)^2}}⋅{\large\frac{(10^{-34})^2}{10^{9}⋅10^{-31}⋅(10^{-19})^2}}\) \({\rm{\large\frac{[J⋅s]^2}{[N⋅m^2]⋅[kg]}}}\)
≒ 0.00529160284044425953275944948597×10-68-9+31+38 \({\rm{\large\frac{[N⋅m⋅s]^2}{[N⋅m^2]⋅[kg]}}}\)
≒ 0.005292×10-8 \({\rm{\large\frac{[N⋅s^2]}{[kg]}}}\)
= 5.292×10-11 \({\rm{\large\frac{[kg⋅(m/s^2)⋅s^2]}{[kg]}}}\)
= 5.292×10-11 [m]
\(r\) = (5.292×10-11)\(⋅n^2\)
でありますが、\(n^2\) に比例していますので \(n\) が大きくなるほど間隔は大きくなっていきます。
また、\(n\) = 1 のときに \(r\) が最小になるわけですが、そのときの値 5.292×10-11m をボーア半径といいます。基底状態のときの軌道半径です。
ついでに電子の速度 \(v\) の値も計算してみます。
『水素原子の軌道半径』で示した②式
\(mv^2\) = \(k_0{\large\frac{e^2}{r}}\)
を変形して、
\(v\) = \(k_0{\large\frac{e^2}{mvr}}\)
これにボーアの量子条件の式
\(mvr\) = \(n{\large\frac{h}{2π}}\)
を代入して、
\(v\) = \(k_0{\large\frac{e^22π}{nh}}\)
= \({\large\frac{2πk_0e^2}{h}}⋅{\large\frac{1}{n}}\)
各定数
\(k_0\) = 8.9876×109 [N⋅m2/C2]
\(e\) = 1.6022×10-19 [C]
\(h\) = 6.6261×10-34 [J⋅s]
を代入しますと、
\(v\) = \({\large\frac{2⋅(3.1416)⋅(8.9876×10^9)⋅(1.6022×10^{-19})^2}{6.6261×10^{-34}}}⋅{\large\frac{1}{n}}\) \({\rm{\large\frac{[N⋅m^2/C^2]⋅[C]^2}{[J⋅s]}}}\)
= \({\large\frac{2⋅(3.1416)⋅(8.9876)⋅(1.6022)^2}{6.6261}}⋅{\large\frac{(10^9)⋅(10^{-19})^2}{10^{-34}}}⋅{\large\frac{1}{n}}\) \({\rm{\large\frac{[N⋅m^2]}{[N⋅m⋅s]}}}\)
≒ (21.877620692726×109-38+34)\(⋅{\large\frac{1}{n}}\) [m/s]
= (21.877620692726×105)\(⋅{\large\frac{1}{n}}\) [m/s]
≒ (2.188×106)\(⋅{\large\frac{1}{n}}\) [m/s]
\(v\) は \(n\) に反比例しています。
外の軌道にいくほど電子の周回スピードはゆっくりになるということです。
さらについでに電子波の波長 \(λ\) の値も計算してみます。
この波長は
\(λ\) = \({\large\frac{h}{mv}}\)
で表されますが、
\(h\) = 6.6261×10-34 [J⋅s]
\(m\) = 9.1094×10-31 [kg] (電子の質量)
\(v\) = (2.1878×106)\(⋅{\large\frac{1}{n}}\) [m/s]
を代入しますと、
\(λ\) = \({\large\frac{6.6261×10^{-34}}{(9.1094×10^{-31})⋅(2.1878×10^6)⋅\frac{1}{n}}}\) \({\rm{\large\frac{[J⋅s]}{[kg]⋅[m/s]}}}\)
= \({\large\frac{6.6261}{(9.1094)⋅(2.1878)}}×10^{-34+31-6}⋅n\) \({\rm{\large\frac{[N⋅m⋅s]}{[kg]⋅[m/s]}}}\)
= \({\large\frac{6.6261}{(9.1094)⋅(2.1878)}}×10^{-9}⋅n\) \({\rm{\large\frac{[kg⋅(m/s^2)⋅m⋅s]}{[kg]⋅[m/s]}}}\)
≒ (0.3325×10-9)\(⋅n\) \({\rm{\large\frac{[(m/s)⋅m]}{[m/s]}}}\)
= (3.325×10-10)\(⋅n\) [m]
外の軌道にいくほど電子波の波長は長くなります。