原子核の基礎知識
原子の中心部には陽子と中性子がある
前項で説明したように原子の中心部を原子核と呼びます。
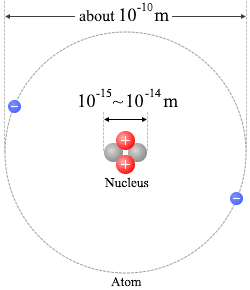 原子核の大きさは原子に比べると非常に小さいです。数万分の1です。
原子核の大きさは原子に比べると非常に小さいです。数万分の1です。
この原子核は核子という粒子からできています
核子は「かくし」です。
格子は「こうし」です。
。核子は2種類あり、一つは陽子 で、もう一つは中性子
で、もう一つは中性子 です。
です。
原子は原子核と電子でできているのでつまり原子は陽子と中性子と電子の3種類の粒子からできているということになります
万物は原子からできているので乱暴な言い方をするとこの世のすべてのものは陽子と中性子と電子からできているということになります。
。
電気的には、陽子は \(+e\) [C] の電荷を持っています。電子の真逆です。中性子は電気的に中性です。電荷を持ちません。そのほか質量等、以下のようになります。
| 電荷 [C] | 質量 [kg] | 記号 | |
| 陽子: | \(+e\) | 1.673×10-27 | p |
| 中性子: | 0 | 1.675×10-27 | n |
| 電子: | \(-e\) | 9.109×10-31 | e- |
陽子、中性子は電子の約1840倍もの重さがあります。そして陽子より中性子の方がごくわずかに重いです。
これらを記号で表すときは陽子が p で、中性子が n です。それぞれ proton 、neutron の頭文字です。電子の記号 e には右上に「 - 」を付けます。
原子の種類は陽子の数によって決まる
原子核の陽子の数は様々で、その数によって原子の特性が変わります。つまり陽子の数が原子の種類を決めます。原子の種類のことを元素といいます。
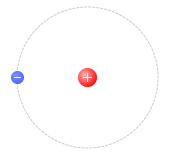 水素原子は中心部に陽子が1個あり、周りに電子が1個あります。中性子は基本的にありません
同位体については下で説明しますが、水素には \(^{1}\rm{H}\)、\(^{2}\rm{H}\)、\(^{3}\rm{H}\)、\(^{4}\rm{H}\)、\(^{5}\rm{H}\)、\(^{6}\rm{H}\)、\(^{7}\rm{H}\) の同位体があり、存在の99%以上が \(^{1}\rm{H}\) で、これには中性子がありません。他の同位体にはあります。
水素原子は中心部に陽子が1個あり、周りに電子が1個あります。中性子は基本的にありません
同位体については下で説明しますが、水素には \(^{1}\rm{H}\)、\(^{2}\rm{H}\)、\(^{3}\rm{H}\)、\(^{4}\rm{H}\)、\(^{5}\rm{H}\)、\(^{6}\rm{H}\)、\(^{7}\rm{H}\) の同位体があり、存在の99%以上が \(^{1}\rm{H}\) で、これには中性子がありません。他の同位体にはあります。
中性子が無い原子は珍しく、\(^{1}\rm{H}\) 以外には \(^{3}\rm{Li}\) だけです。
\(^{1}\rm{H}\) に中性子が無いのは無くても安定するからです。詳しくは下で説明します。\(^{3}\rm{Li}\) に無いのはちょっとイレギュラーです。ですので \(^{3}\rm{Li}\) はほとんど存在しません。
。陽子の電荷は \(+e\) で、電子が \(-e\) であり、2つ合わせて原子は電気的に中性になっています。電子は外れたり加わったりすることがあり、外れればその原子は陽イオン、加われば陰イオンになります。
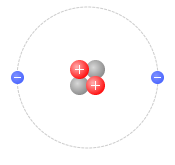 ヘリウム原子は中心部に陽子が2個と中性子が2個あり、周りに電子が2個あります。陽子2個と電子2個で電気的に中性になっています。
ヘリウム原子は中心部に陽子が2個と中性子が2個あり、周りに電子が2個あります。陽子2個と電子2個で電気的に中性になっています。
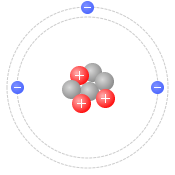 リチウム原子は中心部に陽子が3個と中性子が3個あるいは4個あり、周りに電子が3個あります。陽子3個と電子3個で電気的に中性になっています。
リチウム原子は中心部に陽子が3個と中性子が3個あるいは4個あり、周りに電子が3個あります。陽子3個と電子3個で電気的に中性になっています。
原子というものは(イオン化していなければ)陽子の数と電子の数は同じになっています。中性子の数は様々です(様々といってもだいたいの傾向はあります)。
元素記号
 水素、ヘリウム、リチウム、ベリリウム、以下陽子の数順に並べて表にしたものが元素の周期表です。理科の教科書の表紙裏に載っているやつです。
高校物理では周期表をすべて完璧に暗記する必要はありません
水素、ヘリウム、リチウム、ベリリウム、以下陽子の数順に並べて表にしたものが元素の周期表です。理科の教科書の表紙裏に載っているやつです。
高校物理では周期表をすべて完璧に暗記する必要はありません
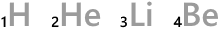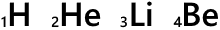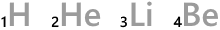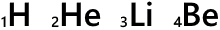 H、He、Li、Be、…というのは元素記号です。
H、He、Li、Be、…というのは元素記号です。
 元素記号の左下の数字は原子番号です。陽子の数がそのまま原子番号になっています。
元素記号の左下の数字は原子番号です。陽子の数がそのまま原子番号になっています。
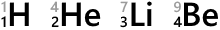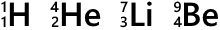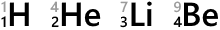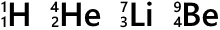 左上に数字を振ることもあり、この数を質量数といいます。陽子の数と中性子の数を単純に足したものです
つまり核子の数です
。質量とは異なります(質量の目安にはなります)。
左上に数字を振ることもあり、この数を質量数といいます。陽子の数と中性子の数を単純に足したものです
つまり核子の数です
。質量とは異なります(質量の目安にはなります)。
陽子の数は元素によって決まっているので原子番号は H のときは必ず 1 だし、He のときは必ず 2 であるし、この数値は表記せずに省略することがあります。
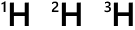 中性子の数は同じ元素でも原子によって異なり(下で説明)、そのことをはっきりさせなければならないときは左上の質量数を表す数値は必ず表記します。
中性子の数は同じ元素でも原子によって異なり(下で説明)、そのことをはっきりさせなければならないときは左上の質量数を表す数値は必ず表記します。
原子番号(=陽子数)、中性子数、質量数を量記号で表すときはそれぞれ \(Z\) 、\(N\) 、\(A\) を用います
\(Z\) はドイツ語で「数」を表す Zahl ツァール から、\(N\) は neutron から、\(A\) は分かりませんが amount ではないかと思います。
。大きさ関係は \(Z + N = A\) となっています。元素記号を \(\rm{X}\) と置いて表現しますと、\(^{A}_{Z}{\large\rm{X}}\) となります
\(N\) は表記しません。
元素記号のアルファベットは大文字で表記します。2文字の場合も第一文字は大文字です。一方、陽子、中性子、電子を表す p、n、e は小文字で表記します。
(さらに詳しく言うと、\(Z\) 、\(N\) 、\(A\) は量記号なので斜体で、元素記号や p、n、e は立体です。あまり気にする必要はないと思いますが。)
(あと、 \(\rm{X}\) は任意のハロゲン元素を示すときにも使われます。ここでは全ての元素という意味で使っています。)
。
水素分子は2個の水素原子が結合したものであり \(\rm{H_{2}}\) と表します。水素の陽イオンは \(\rm{H^{+}}\) と表します。
水素分子も水素の陽イオンも原子核は水素原子のままです。陽子の数も中性子の数も変化してません。化学で習う化学反応も主に電子の振る舞いによるもので、原則的に原子核には変化はありません。逆に原子核の中の中性子の数が多かったり少なかったりすることがあります(同位体のことです)がそれは電子の振る舞いには無関係です。
というわけで、原子核物理分野では主に元素記号の左側上下 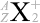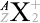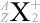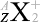 の値が問題になりますが、化学分野では主に元素記号の右側上下
の値が問題になりますが、化学分野では主に元素記号の右側上下 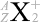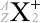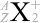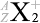 の値が問題になります。元素記号の左側が核子関連で、右側が電子関連です。
の値が問題になります。元素記号の左側が核子関連で、右側が電子関連です。
同位体は陽子数が同じで中性子数が違う原子
同一の原子番号を持ち(=陽子の数が同じ=元素が同じ)ながら中性子の数が異なる原子核を持つ原子もあり といいますか、ほとんどの元素には同位体があります。究極的なことをいいますと全ての元素に同位体があります。 、それらの原子の関係あるいはそれら自体を同位体(アイソトープまたは同位元素)といいます。
また、原子核の種類を陽子、中性子両方の数で分類したものを核種といいます 参考書によっては核種のことを「原子核の種類」といったり「原子の種類」といったりしますが、どちらでも実質的に同じことです。 。
用語がややこしいですが、たとえば以下の①~⑥の原子のうち、
① \(^{1}_{1}\rm{H}\) ② \(^{2}_{1}\rm{H}\) ③ \(^{3}_{1}\rm{H}\) ④ \(^{3}_{1}\rm{H}\)
①~④は同じ元素、⑤と⑥は同じ元素、
記号でなく言葉で表現するときは上記はそれぞれ
① 水素 ② 重水素 ③ 三重水素 ⑤ 炭素12 ⑥ 炭素13
といいます。他にたとえば \(\ce{^16_8O}\) なら酸素16、\(\ce{^17_8O}\) なら酸素17、\(^{35}_{17}\rm{Cl}\) なら塩素35、\(^{37}_{17}\rm{Cl}\) なら塩素37、といいます。水素だけ変則的です。
水素も①を水素1、②を水素2、③を水素3(あるいはトリチウム)ということがあります。
また②の重水素を二重水素ということもあります。さらにいうと②と③を合わせて重水素ということもあります。このとき重水素でないという意味で①を軽水素ということもあります。まだ他にも呼び方があってとてもややこしいです。
原子量は原子の質量とはちょっと違う
原子はとても軽いのでkgより小さい単位を使う
原子核や原子や分子の質量はとても小さいので kg ではなく統一原子質量単位(記号 u
unified atomic mass unit の unified の 頭文字
「ユー」
)という単位が一般的に使われます。
言葉の先頭に「統一」と付くわりにまだ完全に統一された単位となっていません。同位体のこともあるし物理分野と化学分野の都合の違いもあったりでなかなか確定できないようです。いっそのこと kg のままでいいのにと思うところですが、やはり基準みたいなものがあるとわかりやすくて便利です。
現在は以下の3種の単位が使われています。
【ダルトン Da】定義は炭素12の\({\large\frac{1}{12}}\)
【統一原子質量単位 u】定義は炭素12の\({\large\frac{1}{12}}\)
【原子質量単位 amu】定義は複数
古い参考書には amu が載ってたりしますがこれは廃れていきそうです。現在の高校物理の教科書には u が載っているのですが、Da も有力であり今後どうなるかわかりません。
この単位は 1u が炭素12原子1個
\(^{12}_{~~6}\rm{C}\) のことです。炭素の同位体の中でもっとも一般的な原子です。
かつては水素原子や酸素原子を基準としたこともありましたが現在では炭素12原子を基準としています。おそらく炭素12が一番数値が確定しやすいのだと思います。
の質量の\({\large\frac{1}{12}}\)と定められています。炭素12原子は 1mol で 12g です。6.02×1023個で 12×10-3kg です。つまり、
1 [u] = \({\large\frac{12×10^{-3}}{6.02×10^{23}}} × {\large\frac{1}{12}}\)
です。
原子量は存在比を考慮する
元素の質量はいくらかと問われたときに単純に答えるわけにはいきません。たとえば炭素12の質量は 12u ですが炭素には同位体があり炭素13の質量は 13.00u です。これを足して2で割るわけにもいきません。炭素12の方が圧倒的に多く存在するからです。存在する比率を考慮すべきです。元素の質量として妥当なのは各同位体の存在比を考慮した質量の平均値です。この平均値を原子量といいます。
炭素12の存在比は 98.93% で、炭素13の存在比は 1.07% です
天然には炭素14も存在しますが無視できるほど少ないです(下で示す原子量の値は炭素14を含めて計算したとしても変わりません)。炭素12の 98.93% と炭素13の 1.07% で、合わせてほぼ100%です。これらの存在比は地球上のどこで採取してもほぼ変わりません。
他に人工的に合成される同位体もあります。炭素12、13、14以外に現在、炭素8から炭素22までの同位体が合成されています。もちろん人工的に合成された同位体は原子量の計算には組み込まれません。
。平均値を割り出すと以下のようになります。
\(12 × 0.9893 + 13.00 × 0.0107\)
= \(12 × 0.9893 + (12.00 + 1.00) × 0.0107\)
= \(12 × 0.9893 + 12.00 × 0.0107 + 1.00 × 0.0107\)
= \(12 × (0.9893 + 0.0107) + 1.00 × 0.0107\)
= \(12 × (1.0000) + 0.0107\)
= \(12.0107\)
これが炭素の原子量です。単位はありません。[u] を付けたくなりますが、(建前上)原子量は炭素12の\({\large\frac{1}{12}}\)の何倍かを表す量となっています。比です。無次元量です。しかし実質的には質量を表しています。
統一原子質量単位や原子量の定義は年々変わるので厳密な話は覚えきれなくても致し方ありません。しかし少なくとも「質量数」と「原子の質量」と「原子量」の区別はつくようにしてください。
「質量数」は陽子の数と中性子の数を足したものです。個数です。
「原子の質量」は個別の同位体の質量です。たとえば\(^{1}_{1}\rm{H}\)は 1.0078u で、\(^{2}_{1}\rm{H}\)は 2.0141u です。(話の流れによっては原子量のことを原子の質量と言ってしまうこともあるかもしれません)
「原子量」は元素の質量(あるいは質量と言ってはいけないのなら比)であり、同位体の存在比を考慮した平均値です。
| 元素 | 同位体 | 質量[u] | 存在比[%] |
|---|---|---|---|
| 水素 | \(^{1}_{1}\rm{H}\) \(^{2}_{1}\rm{H}\) \(^{3}_{1}\rm{H}\) | 1.0078 2.0141 3.0160 | 99.9885 0.0115 - |
| ヘリウム | \(^{3}_{2}\rm{He}\) \(^{4}_{2}\rm{He}\) | 3.0160 4.0026 | 0.0001 99.9999 |
| 炭素 | \(^{12}_{~~6}\rm{C}\) \(^{13}_{~~6}\rm{C}\) \(^{14}_{~~6}\rm{C}\) | 12 13.0034 14.0032 | 98.93 1.07 - |
| 酸素 | \(^{16}_{~~8}\rm{O}\) \(^{17}_{~~8}\rm{O}\) \(^{18}_{~~8}\rm{O}\) | 15.9949 16.9991 17.9991 | 99.757 0.038 0.205 |
| 塩素 | \(^{35}_{17}\rm{Cl}\) \(^{37}_{17}\rm{Cl}\) | 34.9689 36.9659 | 75.76 24.24 |
| ウラン | \(^{234}_{~~92}\rm{U}\) \(^{235}_{~~92}\rm{U}\) \(^{238}_{~~92}\rm{U}\) | 234.0410 235.0439 238.0509 | 0.0054 0.7204 99.2742 |
陽子同士は反発し合うはずなのに
上で説明したように陽子は + の電荷を持っています。もう一つの核子である中性子は電気的に中性です。これはちょっと不思議なことです。水素以外の元素では陽子が複数あります。陽子同士が反発し合うはずです。原子の中心部にとどまっていられないはずです。
なぜとどまっていられるかというと、陽子同士の静電気力を上回る力がはたらいているからです。この力を核力といいます。核子と核子の間にはたらく力です。静電気力でも万有引力でもない新しい力です。とても強い力です。しかしこれは近距離でしか発揮されない力です。