ある白熱電球に電圧をかけて電流を測定したところ、図3のような結果が得られた。出力電圧 20V の直流電源に、この電球と抵抗値 R の抵抗器をつないだ図4のような回路について考える。
（問3）電圧計で電球にかかる電圧を測ったところ 12V であった。このときの抵抗器の抵抗値 R として最も適当な値を、次の①～⑥のうちから一つ選べ。
① 2.4 ② 3.6 ③ 8.0 ④ 12 ⑤ 27 ⑥ 40
（問4）次に、抵抗器をとりかえて R = 50 Ω にしたとき、電球で 1秒あたりに発生するジュール熱として最も適当な値を、次の①～⑥のうちから一つ選べ。
① 0.28 ② 0.80 ③ 1.1 ④ 1.9 ⑤ 2.8 ⑥ 3.6
#センター08追試
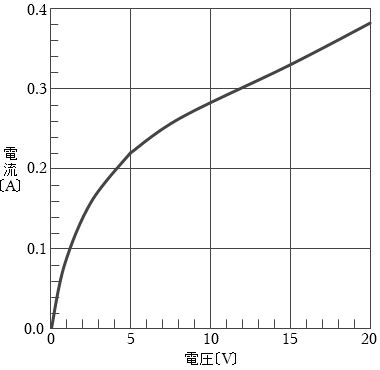
図3のグラフは電球に関してのグラフであって、回路全体に関するグラフではないことに気を付けながら問題を解きます。
（問3）
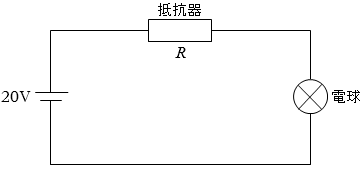
電球にかかる電圧が 12V というのだから、
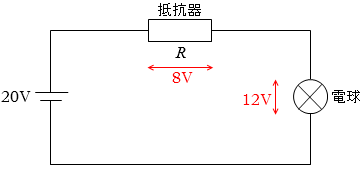
抵抗器にかかる電圧は 20 - 12 = 8.0 [V] です。
また、電球にかかる電圧が 12V ということは、グラフから読み取ると、
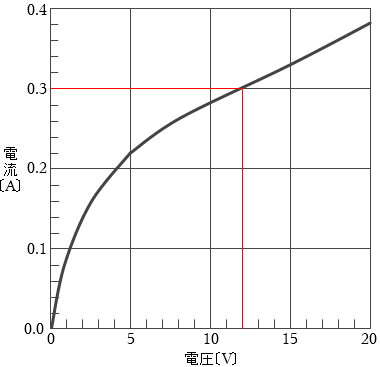
電球に流れる電流は 0.3A と分かります。
電球に流れる電流の大きさと、抵抗器に流れる電流の大きさは同じですから 0.3A です。よって抵抗器の抵抗値 R はオームの法則より、
R = \(\large{\frac{8.0}{0.3}}\) = 26.666… ≒ 27 [Ω]
答は ⑤ 27 です。
（問4）
電球にかかる電圧を v [V] 、電球に流れる電流（＝回路に流れる電流）を i [A] と置きます。
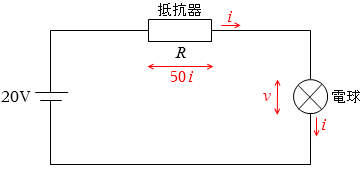
すると、50 [Ω] の抵抗器にかかる電圧はオームの法則より 50i [V] ですので、
20 = 50i + v
という関係式が成り立ちます。変形しますと、
50i = - v + 20
∴ i = - \(\large{\frac{1}{50}}\)v + 0.4
この回路はこの関係式を満たしているはずです。と同時に、i と v は電球にかかる電流と電圧ですので、図3のグラフも満たしているはずです。
この関係式をグラフに書き込むと、
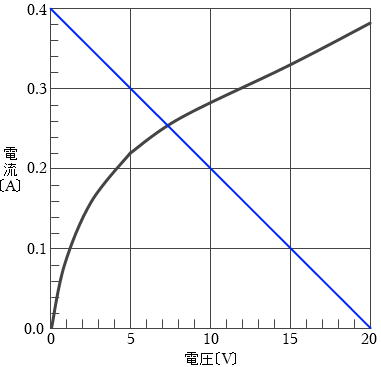（グラフの描き方は分かりますでしょうか。切片が 0.4 で、傾きが - \(\large{\frac{1}{50}}\) です。v=0 のとき i=0.4 で、i=0 のとき v=20 です）
i と v はこの２つの曲線を同時に満たさなければならない、すなわち、実際に電球にかかる電圧と電流は2つの曲線の交点で表される値となります。
グラフの交点を読み取ると、
v = 7.5 [V] 、i = 0.25 [A]
1秒あたりに発生するジュール熱というのは電力のことです。Q = IVt に時間 t を掛ければ IV であり、これは電力 P のことです。
よって、1秒あたりに発生するジュール熱は
i × v = 7.5 × 0.25 = 1.875
答は ④ 1.9 です。