qHBF7

（問3）
図2(a)のPQ間の合成抵抗は

　　　　R₁ + R₂ + R₃ = 10 + 20 + 40 = 70 [Ω]

ここに 10V の電圧が掛かっているから、電流 I_a は、オームの法則より、

　　　　I_a = \(\large{\frac{10}{70}}\) ≒ 0.14285 ≒ 0.14 [A]

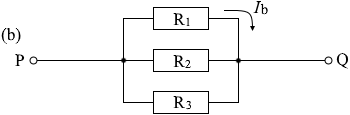
図2(b)の回路では抗R₁、 R₂、 R₃共に 10V の電圧が掛かっているから、R₁を流れる電流 I_b は、オームの法則より、

　　　　I_b = \(\large{\frac{10}{10}}\) = 1.0 [A]

答えは ⑦ です。

（問4）

(a)
　R₁に掛かる電圧は、オームの法則より、10 × 0.14 = 1.4 [V]

　同様に、R₂に掛かる電圧は　20 × 0.14 = 2.8 [V]

　同様に、R₃に掛かる電圧は　40 × 0.14 = 5.6 [V]

電力は電流と電圧を掛けたものだから、

　R₁の消費電力は　0.14 × 1.4 = 0.196 [W]

　R₂の消費電力は　0.14 × 2.8 = 0.392 [W]

　R₃の消費電力は　0.14 × 5.6 = 0.784 [W]

よって消費電力が最も大きいのは R₃ 。

（計算しなくても暗算できる）
電力というのは P = I²R でもあるので、流れる電流が共通なら抵抗 R の大きさに比例します。

(b)
　R₁に流れる電流は、問3で求めたように、1.0 [A]

　問3と同様に、R₂に流れる電流を求めると、\(\large{\frac{10}{20}}\) = 0.50 [A]

　同様に、R₃に流れる電流を求めると、\(\large{\frac{10}{40}}\) = 0.25 [A]

電力は電流と電圧を掛けたものだから、

　R₁の消費電力は　1.0 × 10 = 10 [W]

　R₂の消費電力は　0.50 × 10 = 5.0 [W]

　R₃の消費電力は　0.25 × 10 = 2.5 [W]

よって消費電力が最も大きいのは R₁ 。

（計算しなくても暗算できる）
電力というのは P = \(\large{\frac{V^2}{R}}\) でもあるので、電圧が共通なら抵抗 R の大きさに反比例します。

（余談）
ちなみに、
回路(a)の消費電力は　0.196 + 0.392 + 0.784 = 1.372 [W]

回路(b)の消費電力は　10 + 5.0 + 2.5 = 17.5 [W]

であり、(b)の方が大きいです。同じ複数の抵抗に同じ電圧を掛けるとき、直列に接続するより並列に接続した方が電流も消費電力も大きくなります。