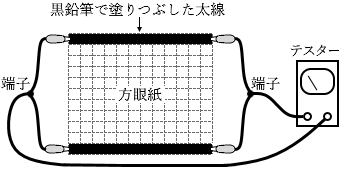
(問1)
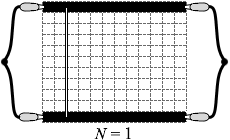
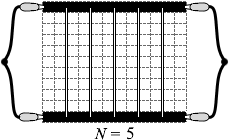
太線が M本のときの抵抗を RM とします。
太線が2本のときの合成抵抗というのは、太線が1本のときの抵抗を2つ並列に接続したものだから、
\(\large{\frac{1}{R_2}}\) = \(\large{\frac{1}{R_1}}\) + \(\large{\frac{1}{R_1}}\)
∴ \(\large{\frac{1}{R_2}}\) = \(\large{\frac{2}{R_1}}\)
∴ R2 = \(\large{\frac{R_1}{2}}\)
太線が3本のときの合成抵抗というのは、太線が1本のときの抵抗を3つ並列に接続したものだから、
\(\large{\frac{1}{R_3}}\) = \(\large{\frac{1}{R_1}}\) + \(\large{\frac{1}{R_1}}\) + \(\large{\frac{1}{R_1}}\)
∴ \(\large{\frac{1}{R_2}}\) = \(\large{\frac{3}{R_1}}\)
∴ R3 = \(\large{\frac{R_1}{3}}\)
同様に、太線が M本のとき、
∴ RM = \(\large{\frac{R_1}{M}}\)
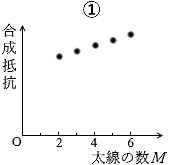
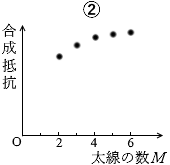
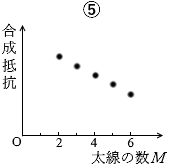
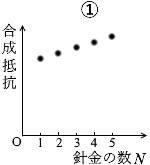
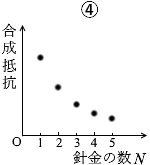
つまり、合成抵抗は M に反比例します。反比例になっているグラフは ④ です。
(問2)
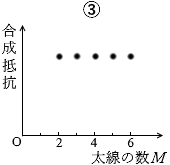
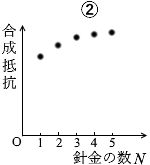
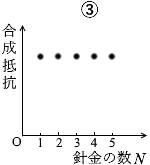
この場合、針金には電流は流れないので針金の本数が何本になっても合成抵抗の大きさは変わりません。答えは ③ です。
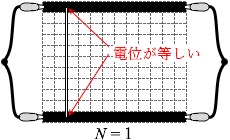
針金の両端は電位が等しく、針金には電位差が生まれないので電流が流れません。もし、針金の接続の仕方が直角ではなく斜めだったりすれば、電位差が生じるので電流が流れます。
このことを川の流れにたとえて説明しますと、
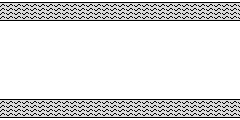 標高が等しい2つの川が平行に流れているとき、
標高が等しい2つの川が平行に流れているとき、
直角に水路を渡しても新たな水の流れは起こりません。
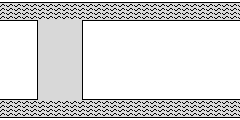 水路に水は満たされますが流れは起こりません。水路の水はあっちに行こうとする力とこっちに来ようとする力がちょうどつり合ってどちらにも動きません。ホイートストンブリッジの面白い現象と同じです。
水路に水は満たされますが流れは起こりません。水路の水はあっちに行こうとする力とこっちに来ようとする力がちょうどつり合ってどちらにも動きません。ホイートストンブリッジの面白い現象と同じです。
2つの川のうちどちらかが強かったり、あるいは水路を斜めに渡せば水流は起こります。
(問3)
直列に接続された抵抗の合成抵抗は各抵抗を単純に足し合わせたものであるから、
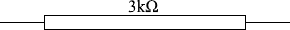 3.0kΩ の1本の抵抗は
3.0kΩ の1本の抵抗は
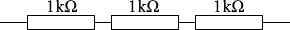 1.0kΩ の抵抗が3つ連なっているとみなすことができます。
1.0kΩ の抵抗が3つ連なっているとみなすことができます。
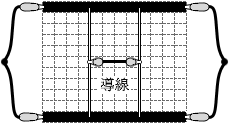
ですので、図4は以下のように描き変えることができます。
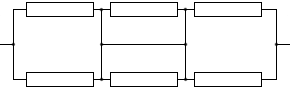
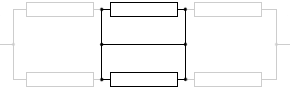 このとき、真ん中の2つの抵抗には電流が流れません。電流は導線部分のみを通ります。導線はいちおう抵抗が 0 ということになっていて、抵抗が少しでもある部分と、抵抗が 0 の部分の二つの経路がある場合、電流は抵抗 0 の方だけを通ります。
このとき、真ん中の2つの抵抗には電流が流れません。電流は導線部分のみを通ります。導線はいちおう抵抗が 0 ということになっていて、抵抗が少しでもある部分と、抵抗が 0 の部分の二つの経路がある場合、電流は抵抗 0 の方だけを通ります。
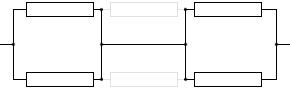 つまり、図4は事実上、左図のような回路になります。
つまり、図4は事実上、左図のような回路になります。
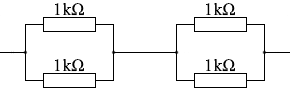 左半分の部分の合成抵抗は、1.0kΩ の抵抗と 1.0kΩ の抵抗の並列接続だから、0.5kΩ であり、
左半分の部分の合成抵抗は、1.0kΩ の抵抗と 1.0kΩ の抵抗の並列接続だから、0.5kΩ であり、
右半分の部分も同様に 0.5kΩ であり、
全体の合成抵抗は、0.5kΩ の抵抗と 0.5kΩ の抵抗が直列接続されたものだから、 1.0kΩ となります。図4の回路は、1.0kΩ の抵抗が一つあるのと一緒ということです。
 ・・・ →
・・・ → 
 ・・・ →
・・・ → 

 標高が等しい2つの川が平行に流れているとき、
標高が等しい2つの川が平行に流れているとき、 水路に水は満たされますが流れは起こりません。水路の水はあっちに行こうとする力とこっちに来ようとする力がちょうどつり合ってどちらにも動きません。ホイートストンブリッジの
水路に水は満たされますが流れは起こりません。水路の水はあっちに行こうとする力とこっちに来ようとする力がちょうどつり合ってどちらにも動きません。ホイートストンブリッジの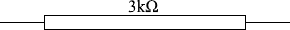 3.0kΩ の1本の抵抗は
3.0kΩ の1本の抵抗は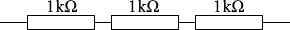 1.0kΩ の抵抗が3つ連なっているとみなすことができます。
1.0kΩ の抵抗が3つ連なっているとみなすことができます。
 このとき、真ん中の2つの抵抗には電流が流れません。電流は導線部分のみを通ります。導線はいちおう抵抗が 0 ということになっていて、抵抗が少しでもある部分と、抵抗が 0 の部分の二つの経路がある場合、電流は抵抗 0 の方だけを通ります。
このとき、真ん中の2つの抵抗には電流が流れません。電流は導線部分のみを通ります。導線はいちおう抵抗が 0 ということになっていて、抵抗が少しでもある部分と、抵抗が 0 の部分の二つの経路がある場合、電流は抵抗 0 の方だけを通ります。 つまり、図4は事実上、左図のような回路になります。
つまり、図4は事実上、左図のような回路になります。 左半分の部分の合成抵抗は、1.0kΩ の抵抗と 1.0kΩ の抵抗の
左半分の部分の合成抵抗は、1.0kΩ の抵抗と 1.0kΩ の抵抗の