ホイートストンブリッジ

ブリッジ回路

途中で橋を渡したような形の電気回路をブリッジ回路といいます。

面白い現象

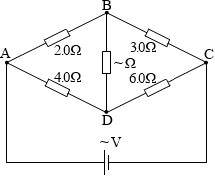
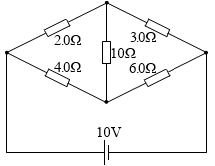左図のようなブリッジ回路では面白い現象が起きます。

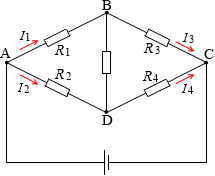
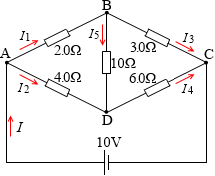左図のように符号を振り、電流の向きを仮設定し、各抵抗を流れる電流の大きさを『キルヒホッフの法則の例題』と同じ要領で求めてみます。

（キルヒホッフ第１法則の式）
（分岐点Aについて） I = I₁ + I₂　　……①
（分岐点Bについて） I₁ = I₃ + I₅　　……②
（分岐点Cについて） I₃ + I₄ = I　　……③
（分岐点Dについて） I₂ + I₅ = I₄　　……④

（キルヒホッフ第２法則の式）
（起電力→A→B→C→起電力） 10V - 2.0Ω×I₁ - 3.0Ω×I₃ = 0　　……⑤
（起電力→A→D→C→起電力） 10V - 4.0Ω×I₂ - 6.0Ω×I₄ = 0　　……⑥
（A→B→D→A） - 2.0Ω×I₁ - 10Ω×I₅ + 4.0Ω×I₂ = 0　　……⑦
（B→C→D→B） - 3.0Ω×I₃ + 6.0Ω×I₄ + 10Ω×I₅ = 0　　……⑧

これらの内の、計算が楽になりそうな②式、④式、⑤式、⑥式、⑦式 の５式を用いて、I₁、I₂、I₃、I₄、I₅ を求めてみます。

　　　　I₁ = I₃ + I₅　　……②
　　　　I₂ + I₅ = I₄　　……④
　　　　10 - 2.0I₁ - 3.0I₃ = 0　　……⑤
　　　　10 - 4.0I₂ - 6.0I₄ = 0　　……⑥
　　　　- 2.0I₁ - 10I₅ + 4.0I₂ = 0　　……⑦

②式を⑤式に代入して、
　　　　10 - 2.0I₁ - 3.0(I₁ - I₅) = 0
　　　　- 5.0I₁ + 3.0I₅ = - 10
　　　　5.0I₁ - 3.0I₅ = 10　　……⑤'

④式を⑥式に代入して、
　　　　10 - 4.0I₂ - 6.0(I₂ + I₅) = 0
　　　　- 10I₂ - 6.0I₅ = - 10　　……⑥'

⑦×5　 - 10I₁ - 50I₅ + 20I₂ = 0
⑤'×2　　　　　10I₁ - 6.0I₅ = 20
⑥'×2　　　　 - 20I₂ - 12I₅ = - 20

３式を足しますと、
　　　　- 50I₅ - 6.0I₅ - 12I₅ = 20 - 20
　　　　- 68I₅ = 0
　　　　I₅ = 0

⑤'式、⑥'式に代入して、
　　　　I₁ = 2A
　　　　I₂ = 1A

②式、④式に代入して、
　　　　I₃ = 2A
　　　　I₄ = 1A

各電流の値が負にならなかったので電流の向きは仮設定の向きの通りです。I₅ = 0 です。BD間は導線でつながっているのに電流が流れないのです。

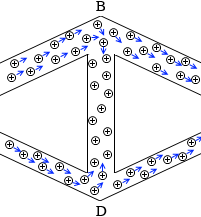
この回路における電流と電位差のイメージ図を描いてみます。

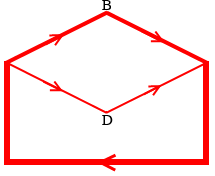電流のイメージ図です。

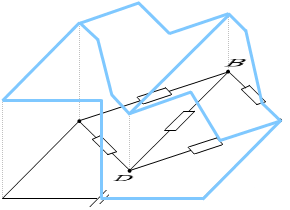電位差のイメージ図です。

B点の電位の高さとD点の電位が高さが同じになって、BD間に電流が流れなくなっています。

これは電荷の通り道がふさがれたわけではなく、B点での下向きの圧力とD点での上向きの圧力が等しくなって、BD間の電荷が動かなくなった、という状態です。

そしてこれは、起電力の大きさとBD間の抵抗の大きさには無関係です。上の計算式においてそれら２つの値を変更しても I₅ の値は 0 になります。

ホイートストンブリッジ

左図のように各抵抗に符号を振ります。

BD間に電流が流れないとき、

　　　I₁ = I₃
　　　I₂ = I₄

そして、B点の電位とD点の電位が等しいのだから、

（AB間の電圧=AD間の電圧）　R₁I₁ = R₂I₂　　……ⓐ　（オームの法則）
（BC間の電圧=DC間の電圧）　R₃I₃ = R₄I₄　　……ⓑ

ⓐ式を変形して、
　　　　\(\large{\frac{R_1}{R_2}}\) = \(\large{\frac{I_2}{I_1}}\)　　……ⓐ'

ⓑ式に I₁ = I₃、I₂ = I₄ を代入して変形すると、
　　　　R₃I₁ = R₄I₂
　∴　　\(\large{\frac{R_3}{R_4}}\) = \(\large{\frac{I_2}{I_1}}\)……ⓑ'

ⓐ'式、ⓑ'式 より、
　　　　\(\large{\frac{R_1}{R_2}}\) = \(\large{\frac{R_3}{R_4}}\)

各抵抗がこのような関係を満たすとき、BD間（回路のブリッジ部分）には電流が流れません。上で例示した電気回路の各抵抗はこの関係を満たしています。

このような電気回路をホイートストンブリッジ ＊19世紀のイギリスの物理学者チャールズ・ホイートストンが実用化しました。
　閉じるといいます。

この式は R₂ と R₃ を入れ替えても成り立つので \(\large{\frac{R_1}{R_3}}\) = \(\large{\frac{R_2}{R_4}}\) と間違って覚えても大丈夫です。R₂ と R₄ は入れ違えて覚えてはダメです。R₁R₄ = R₂R₃ と覚えるのはOKです。

電流計、電圧計無しで抵抗値を測定できる

抵抗器の抵抗値を知りたいときは、電圧と電流を測定して、オームの法則による計算で抵抗値を求めればいいのですが、ホイートストンブリッジを用いれば、その必要がありません。電流計、電圧計は精密な測定が難しいですが、ホイートストンブリッジを用いると抵抗値が正確に測定できます。

しかし、（抵抗値の分かっている）抵抗器２つ、可変抵抗器、検流計が必要です。

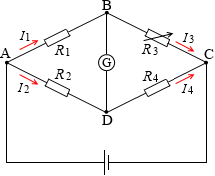左図の 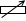は可変抵抗器です。目盛りに合わせて抵抗値を変えられます。

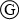というのは検流計です。わずかな電流の有無、電流の向きを検知します。ガルバノメーターともいいます。 という記号を用いることもあります。

４辺のうちの２箇所に既知の抵抗器、１箇所に可変抵抗器、残りの１箇所に未知の抵抗器を接続し、検流計の値が 0 になったときの可変抵抗器の値を読み取り、

３つの抵抗の値を　\(\large{\frac{R_1}{R_2}}\) = \(\large{\frac{R_3}{R_4}}\)　に代入して未知の抵抗器の抵抗値を割り出します。

メートルブリッジ

ホイートストンブリッジをもうちょっと工夫すると既知の抵抗器を２つでなく１つだけ使うことによって未知の抵抗器の抵抗値を測定することができます。可変抵抗器も要りません。

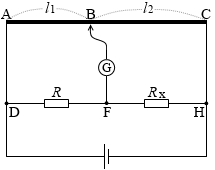左図のようにAC間に材質が一様で太さが一定の抵抗線をつなぎ、DF間に既知の抵抗をつなげます。

検流計の値が 0 になるようにB点をスライドさせます。ABの長さ：BCの長さ = l₁：l₂ とします。

『抵抗率』項で説明しましたが、抵抗というものは　R = ρ⋅\(\large{\frac{l}{S}}\)　という式で表せます。ρ は材質のことで、l は長さ、S は太さのことです。つまり今の場合、AB間の抵抗とBC間の抵抗の比は長さの比です。

そして、先の　\(\large{\frac{R_1}{R_2}}\) = \(\large{\frac{R_3}{R_4}}\)　という式は

　　　　R₄ = \(\large{\frac{R_3}{R_1}}\)R₂

と変形でき、今、 \(\large{\frac{R_3}{R_1}}\) = \(\large{\frac{l_2}{l_1}}\)　であるのだから代入して、

　　　　R₄ = \(\large{\frac{l_2}{l_1}}\)R₂

であります。上で示したホイートストンブリッジの図と上図を見比べて、R₄ を R_x に、R₂ を R に書き換えると、

　　　　R_x = \(\large{\frac{l_2}{l_1}}\)R　　（ R：R_x = l₁：l₂ とも書けます。こちらの方がイメージしやすいかも）

となります。l₁ と l₂ の比と既知の抵抗 R の値が分かれば、未知の抵抗 R_x の値が分かります。たとえば、既知の抵抗が 10Ω で l₁：l₂ = 1：2 であれば未知の抵抗は 20Ω です。

このような回路をメートルブリッジといいます。